Introduction to high level Computer programming

INTRODUCTION TO
COMPUTER
PROGRAMMING
Samuel kizito

Computer programming
 Computer Programming is defined as the process
of creating computer software using a
programming Language. Computer programs are
written by Human individuals(Programmers)
 A computer program is a step by step set of
instructions that a computer has to work through
in a logical sequence in order to carry out a
particular task. The computer executes these
instructions (obeys the instructions) when told to
do so by the user.

Programming Languages
 Programming languages are the vocabulary and
set of grammatical rules for instructing a computer
to perform specific tasks. There are many different
types of programming languages each having a
unique set of keywords (words that it
understands) and a special syntax (grammar)for
organising program instructions.

Syntax
 Syntax refers to the spelling and grammar of a
programming language. Each program defines its
own syntactical rules that control which words the
computer understands, which combinations of
words are meaningful, and what punctuation is
necessary. Text-based programming languages are
based on sequences of characters, while visual
programming languages are based on the spatial
layout and connections between symbols (which
may be textual or graphical).

Example of a program code (small
basic)
 TextWindow.Writeline("enter the
Temperature in fahrenheit ")
 fahr = TextWindow.ReadNumber()
 celsius = (5 * (fahr - 32) / 9)
 TextWindow.WriteLine("This Temperature
in celcius is " + celsius +" degrees")

Small Basic
 TextWindow.Write("Enter the temperature today (in
F):")
 temp = TextWindow.ReadNumber()
 If temp > 100 Then
 TextWindow.WriteLine("It is pretty hot.")
 ElseIf temp > 70 Then
 TextWindow.WriteLine("It is pretty nice.")
 ElseIf temp > 50 Then
 TextWindow.WriteLine("Don't forget your coat.")
 Else TextWindow.WriteLine("Stay home.")
 EndIf

 There are many computer programming languages
and so the programmer will have to decide which
one to use for solving a particular problem. These
languages must be learnt just as Swahili, English or
French etc.

Levels of programming languages
 Programming languages are classified into five
major categories: machine languages (first
generation languages), assembly languages
(second generation languages), third generation
languages, fourth generation languages, and
natural languages. Machine and assembly
languages are referred to as low level languages;
third generation, fourth generation and natural
languages are categorised as high level languages.

 A low level language is machine dependent; that
is, it is written to run on one particular computer. A
high level language is machine independent, which
means the high level language code can run on
many different types of computer.
 There are two types of low-level programming
languages: Machine Language and Assembly
Language.

Machine language – First
Generation Language (1GL)
 The machine language writes programs using the
machine code of 1s and 0s, which is directly
understood by the computer.
 The main problems with using machine code
directly are that it is very easy to make a mistake,
and very hard to find it once you realise the
mistake has been made.

Characteristics of 1GL
 Fastest to execute because it is already in the language that the
computer can understand
 Difficult to interpret (requires the aid of a reference manual to
interpret the meaning of each code)
 Easy to make mistakes in the sequence of 1s and 0s; replacing a 1
for a 0 can result in the wrong command/instruction being executed
 It is difficult to identify mistakes made
 Time-consuming and tedious to write
 Machine dependent
 Programing becomes more difficult as the complexity of the
program increases

Assembly language – Second
Generation Language (2GL)
Assembly language is written using mnemonic codes
(abbreviated English words) or short codes that
suggest their meaning and are therefore easier to
remember. These codes represent operations,
addresses that relate to main memory, and storage
registers of the computer. Typical codes might be:
LDA, STO, ADD, NOP, etc.

An example of a program code to add and store two
numbers would be:
LDA A, 20 : load accumulator A with the value 20
ADD A, 10 : add the value 10 to accumulator A
STO B, A : store contents of accumulator A into
storage register B
NOP: no operation (stop here)

Characteristics of 2GL
 As with machine language, assembly language is machine
dependent.
 Assembly language, being machine dependent, is faster and
more efficient in the use of hardware than high-level
programming languages.
 Assembly languages have to be translated into machine
language by language translators known as assemblers for
the processor to understand.
 Easier to write than machine language
 The code is not very easy to understand, hence the
introduction of high level programming languages.

High-level programming
languages
High level programming language is defined as one that
is machine independent and uses variables and
objects, Boolean expressions, functions, loops, arrays,
threads, locks which are similar to their meaning
(abstraction).
 High-level languages have evolved over the years and
can be grouped into five categories: Third Generation
Languages (3GL), Fourth Generation Languages (4GL),
Object Oriented Programming Languages (OOP), Fifth
Generation Languages (5GL) and Scripting Languages

 These languages are problem oriented, so they are
machine independent.
 Since high-level languages reflect the logic and
procedures used in a human algorithm, the programmer
is able to concentrate on developing task algorithms
rather than on how the computer will carry out the
instructions.
 the programmer must still specify a complete set of
detailed instructions. The words and grammar of high-
level languages are English-like and this makes the
programs more readable and easy to write.

 high-level languages are machine independent (they can be
used on different computer systems); Since the syntaxes of
high-level languages are standardised, the languages are
portable.
 A high-level language is governed by a strict syntax (set of
grammatical rules).
 they are easier to read, write, and maintain.
 They also permit faster development of large programs.
 programs written in a high-level language must be translated
into machine language by a compiler or interpreter.

Characteristics of high-level
languages
 They are machine independent hence portable
 They are user friendly and easy to learn
 High-level language programs are easy to debug
 They are more flexible hence they enhance the creativity of
the programmer, increasing productivity
 They are executed much slower than low-level programming
languages
 They have to be translated into machine code before
execution, this is done by compilers and Assemblers.
 One instruction translates into several machine code
instructions

Assemblers and Compilers
 Assemblers and Compilers are programs that
convert high level languages into machine code.
 A Compiler is a program that converts the entire
source code(compiles it) into machine language at
one time before the computer can run the
program at a later time. While compiling the
source code into machine code, it checks that the
syntax is properly written by the programmer for
the programmer to debug the program.

 The interpreters are programs that translates the high level
program code one statement at a time, that is, it reads a code
statement, converts it to one or more machine language
instructions, and then executes the instruction before moving
translating the next code statement in the program. If there is
any error in the statement, the programmer can correct the
error before the interpreter evaluates the next statement.
 Interpreters are slower than Compilers because interpreters
convert a statement at a time and runs it before moving to the
next line.

Object-Oriented programming
(OOP)
 Object-oriented programming (OOP) is a programming
language model organized around objects and data.
 In OOP, the programmer packages the data and the
program procedures into a single unit called an object.
The procedures in the object are called
Operations(Methods or behavior), and the data
elements are called attributes(Variables); this means
that a part from looking at the data structure, the
methods associated with that object used to modify
the object’s attributed must be considered.

 A method is an operation or function which can
modify an object’s behavior i.e. that changes an
object by manipulating its variables, a function is a
sequence of commands or programming code that
returns a value (sends a result back). Think of it as
"What method would you use to add two numbers
together?"

 The concept of packaging methods and attributes into a single
object is what is known as encapsulation(information hiding)
 And Object may be part of a larger category of objects called a
Class; every object in a class share the similar methods and
attributes as the original object. Each class can have one or more
lower levels called sub-classes, the higher level class is called a
super class.
 Each subclass inherits the methods and attributes of the objects
in its super-class. This concept of the lower levels inheriting
methods and attributes of higher levels is called inheritance.

Illustration of relationships
between classes and objects

Major high level programming
languages used
 FORTRAN (FOTmula TRAnslator)developed in the
late 1950s developed to design scientific
applications
 COBOL (Common Business Oriented Language)
developed in early 1960s to develop business
applications.
 RPG (Report Program generator) was developed in
early 1960s to assist in generating reports and
complex calculations.

 BASIC (Beginner’s All-purpose symbolic instruction code)
developed in mid 1960 Basic versions include MS-BASIC,
QBASIC, SmallBASIC and visual basic.
 Pascal was developed in the late 1960s for the purpose
of teaching structured programming concepts
 C developed in the early 1970s to write system software
 Ada was developed in the late 1970s originally
developed to meet the needs of embedded computer
systems

 C++ developed in the 1980s is an object-oriented
language mainly to develop application software
 Note that in addition to the major languages
discussed above, there are many other
programming languages that have been developed
such as JavaScript, and Python

Language Translators
 Language translators are system programs that
convert assembly language and high-level
language into the machine language.
 The computer does not understand assembly
languages or high-level languages. Computers
work in machine code or machine language.

Source code
 Source code is a program code of either an
assembly language or high-level language that the
programmers write in a program editor. Source
code cannot be understood by the computer until
it has been translated into machine code.

Object code
 Object code is a program code in machine-
readable form (a source program that has been
translated).

Assemblers
 The assembly-language program must be
translated into machine code by a separate
program called an assembler. The assembler
program recognises the character strings that
make up the symbolic names of the various
machine operations, and substitutes the required
machine code for each instruction.

Compilers
Compilers are language translators that translate
high-level languages into machine code.
A compiler translates the entire program (source
code) to machine code, and then the code is
executed. The translated codes are known as object
codes and are saved as a file on disk. The object code
(machine code) stored on disk has an EXE file name
extension. It is then loaded or linked (stored in
memory) and executed

Interpreters
 Interpreters are language translators that translate
high-level language into machine code. An
interpreter translates and executes one instruction
at a time as it is encountered. The machine codes
are not saved after execution

The program development life
cycle (PDLC)
During the development of a program there are
several stages. These can be described by the
Program Development Life Cycle (PDLS)which
has several steps which lead to the solution of
the problem.

PDLC is the continuous process that consists of
five/six general steps:
1. Analyse problem
2. Design program
3. Code program
4. Test program
5. Formalise program
6. Maintain program

Problem analysis
 This involves problem recognition, which involves
identifying the need to overcome a given problem
for example, the need for a school to process
students marks and grade accurately at the end of
term and problem definition, which involves
identifying the users program objectives, desired
inputs, outputs, and processing.

Defining the problem
In defining the problem there must be no ambiguity. The
problem should be clear and concise and have only one
meaning.
Examples of unambiguous problems are:
i) Calculating the price of an item after a 10% discount
ii) Converting a temperature from ° C to ° F
iii) Computing the average rainfall for the month of May
in a certain place.

Analysing the problem
 In order to develop an algorithm to accomplish a
certain task you must analyse the task as a
sequence of instructions that can be performed by
the computer.
 These instructions can be divided into three main
parts: input and storage instructions, processing
instructions, and output instructions.

Input and storage instructions
 These instructions allow information or data to be
accepted by the computer. The input is
information that is needed by the computer to
solve the problem. Words such as ‘Enter’, ‘Input’
and ‘Read’ within problem statements usually
indicate what data the computer requires.

What are the input and storage instructions here?
Read the price of an item and calculate the discount
of 10%.
Enter the name and year of birth of a person and
calculate the person’s age.
Input the length of a side of a square tile and find
the area.

Let’s analyse these instructions to determine the
inputs and what we need to store:
Read and store the price of an item.
Enter the name and year of birth of a person.
Input the length of the side of a square tile.

Processing instructions
 These instructions manipulate the input data. They
involve calculations, that is, mathematical
operations (e.g. addition, subtraction,
multiplication and division), repeating instructions,
selecting instructions and comparison instructions.
They also include commands and constructs.

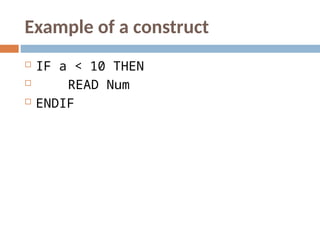
 A command is a word that instructs the computer
what must be done to accomplish a specific task.
Commands are specific to a particular
programming language: for example, WRITE,
PRINT, READ, INPUT, etc.
 A construct is a group of instructions that work
together with commands to accomplish a specific
task. An example is the ‘IF-THEN’ construct:

Example of a construct
 IF a < 10 THEN
 READ Num
 ENDIF

What are the processing instructions here?
Read the price of an item and calculate the new
price after a 10% discount.
Enter a temperature in degrees Celsius and convert
it to degrees Fahrenheit.
Input the name and year of birth and compute and
print the age of a person.

Let’s analyse these instructions to determine what
we need to process.
Calculate the new price after a 10% discount.
Convert it to degrees Fahrenheit.
Compute the age of a person.

Repeating and comparison
statements
Comparison/selection/decision statements involve
determining whether a condition is true or false in order
to perform a set of instructions.
For example:
Read the weekly hours worked by an employee. If the
hours worked are greater than 40, then calculate the
overtime salary at 1.5 times the standard hourly rate of
$1.75, for those hours over 40.
The condition that is checked is the number of hours
worked to determine if it is more than 40.

Repeat statements/loops/iterations are used when a
problem has to be done a number of times.
For example:
Read the marks for three subjects, English, Maths
and ICT for each student; find the average mark of
each student in a class of 15, over the three subjects.
The process of finding the average for the three
subjects has to be repeated 15 times.

Output instructions
These instructions allow information to be displayed on
the screen. Problem statements that include key words
like ‘print’, ‘output’, ‘display’, ‘return’ and ‘write’ indicate
what data should be output to the screen.
What are the output statements here?
Enter the name and year of birth of a person and
compute and display the age of the person.
Write an algorithm to print a conversion table of
degrees Celsius to degrees Fahrenheit, 10 C to 20 C
inclusive.

 Let’s analyse these instructions to determine what
we need to output.
 Display the age of the person.
 Print a conversion table.

Program design
 This is the actual development of a program’s
processing logic. The program’s processing logic is
called its algorithm. An algorithm is a sequence of
instructions which, if followed, produces a solution
to the given problem. At the end of each
instruction, there is no question as to what needs
to be done next, and the instructions eventually
come to an end. An algorithm is written using
special rules and statements

Example of an algorithm
Algorithm:
Read student name and marks obtained.
Calculate total marks and average marks.
Write student name, total marks, average marks.

Program design involves three tasks:
(i) grouping the program activity into modules
(ii) develop a solution algorithm for each module.
An algorithms are well defined rules for solving a
problem
(iii) test the solution algorithm

 The first task that involves grouping tasks into modules
focuses on what must be done (requirements) where
the Top-bottom design is used. This involves breaking
down the program into smaller, manageable
components represented graphically on a hierarchy
chart; the top most showing the main module referred
as the main routine, which is then subdivided into
smaller sections also referred to as sub-routines.
 Each module is represented by a rectangle labeled by
its name.

Design details using Pseudo-code,
flowcharts and control structures
 Once the essential logic of the program has been
determined through the use of top-down
programming and hierarchy charts, you can now
work on the details. The two ways to show
program details are writing the details using
pseudocode or drawing the details using
flowcharts, or both.


Pseudo-code
 A Pseudo-code is an algorithm that models or
resembles the real programming language of the
computer. A Pseudo-code can also be defined as a
tool for designing a program in a narrative form
using human language statements to describe the
logic and processing flow.

Pseudocode
START
READ student name, mark1, mark2, mark3,
mark4
Totalmarks = mark1 + mark2 + mark3 +
mark4
Averagemark = Totalmarks / 4
PRINT student name, totalmarks,
averagemarks
STOP

Pseudo-code commonly used
keywords
 Several keywords are often used to indicate
common input, output, and processing operations.
 Input: READ, OBTAIN, GET
Output: PRINT, DISPLAY, SHOW, writeline
Compute: COMPUTE, CALCULATE, DETERMINE
Initialize: SET, INIT
Add one: INCREMENT, BUMP

Program flow chart
 A program flowchart is a diagrammatic
representation of a program’s processing logic. It
uses standard symbols called ANSI symbols (called
after the American National Standards Institute
that developed them) and short statements that
describe various activities. A flowchart shows how
your program works before you begin actually
coding it.

AN EXAMPLE OF A FLOW CHART
Begin
ENTER TWO
NUMBERS;A,B
CALCULATE SUM=A+B
AVERAGE = SUM/2
AVERAGE
>=60?
GRADE =“A”
PRINT
SUM,AVERAGE
AND GRADE
END
GRADE = “B”

Structured program designs
 When designing a program, you must reason through the
problem to determine the correct logic. The logic of a
program can be established through the use of control
structures. Structure design involves identifying the
logical order of the procedure required to accomplish the
task described in a given module. This procedure is what
is known as the solution algorithm or program logic.
 Control structures or logic structures/constructs control
the logic sequence in which computer program
instructions are executed.

 Four basic control structures are used to form the
logic of a program in structured program design:
sequence, selection, case and iteration (loop).

The Sequence control structure
 The sequence structure is used to show a single
action or one action followed sequentially by
another e.g. reading a record, followed by
calculating totals and averages and then printing
the averages.

The Selection control structure (if-
then-else)
 Selection is a process that allows a computer program
to compare values and then decide what course of
action to take based on a certain condition.
 The selection structure therefore is used to tell the
program which action to take next, based on a certain
condition; when the condition is evaluated, its result is
either true or false : if the result of the condition is true,
then one action is performed; if the result of the
condition is false, a different or no action is performed.

 For example, a condition that if the average mark
is 50 and above, the student is passed, or else, the
student fails. i.e. if a condition is true, then do one
thing, else do another.
 Because of the above, the selection structure is
also known as the if-then-else control structure.

 IF score >= 60 THEN
 Comment = "Pass"
 ELSE
 Comment = "Fail"
 ENDIF
 PRINT comment

Selection control structure
flowchart
Test
condition
THEN statement
ELSE statement
No
Yes

If ..then.. else
 If(age <30)Then
 TextWindow.WriteLine("too young
")
 Else
 TextWindow.WriteLine(“too old ")
 endif

 If (Clock.Hour < 12) Then
 TextWindow.WriteLine("Good
Morning World")
 EndIf
 If (Clock.Hour >= 12) Then
 TextWindow.WriteLine("Good
Evening World")
 EndIf

Case control structure
 The case control structure is a variation of the
selection structure that involves more than a single
yes-or-no decision. The case structure allows
several alternatives or cases to be presented. The
case control structure saves the programmer the
trouble of having to indicate a lot of separate IF…
THEN…ELSE conditions.

Example of an IF…THEN…ELSE structure involving several alternatives:
IF score <= 100 AND score >= 80 THEN
grade = "A"
ELSE IF score >= 75 AND score <= 79 THEN
grade="A-"
grade = "B+"
grade = "B"
grade = "B-"
grade = "C+"”
grade = "C"
ELSE
grade="F"
ENDIF
PRINT grade

Example of case structure
involving several alternatives
CASE score OF
 80 – 100: grade = "A"
 75 - 79: grade ="A-"
 70- 74: grade = "B+"
 65 - 69: grade = "B"
 60 - 64: grade = "B"”
 55- 59: grade = "C+"
 50- 54: grade = "C"
 0-49: grade="F"
END CASE
PRINT grade

 The other possible selection control structure is
known as a case control structure which is used
where a condition can yield one of more than two
possibilities. Using the
If....Then....ElseIf statement.

If....Then...ElseIf Statement
 If there are more than two alternative choices, using
just If....Then....Else statement will not be enough. In order to provide
more choices, we can use the If....Then...ElseIf Statement. The general
format for the if...then.. Else statement is
 If (condition) Then
 expression
 ElseIf condition Then
 expression
 ElseIf condition Then
 expression
 Else
 expression
 End If

 When executing a block If (second syntax), condition is
tested. If condition is True, the statements
following Then are executed. If condition is False,
each ElseIf (if any) is evaluated in turn. When
a True condition is found, the statements following the
associated Then are executed. If none of
the ElseIf statements are True (or there are noElseIf clauses),
the statements following Else are executed. After executing
the statements following Then or Else, execution continues
with the statement following End If.

The Repetition control structure
(Iteration)
 The repetition control structure is also known as
the looping, or iteration control structure. It is
used when a set of actions are to be performed
repeatedly as long as a certain condition is met.
 Iteration or looping is where a process(routine) is
done repeatedly. There are two forms iteration;
the Conditional and the unconditional looping.

Conditional looping
 A conditional looping is one that is repeated until a
specified condition is met. It uses a selection
process to decide whether or not to carry on a
process.
 Conditional looping are of two forms;
 Do-while and do-until

The do-while repetition control
structure
 This control repeats as long as a condition is true,
it tests the condition at the beginning of the loop
and, if the result of the condition is true, the
action(s) inside the loop is executed. Then the
program loops back and tests the condition again,
if the result is still true, the action(s) inside the
loop is executed again. This continues until the
condition becomes false.

The Do -While loop
 In the program below, we assign the value 100 to
number and run the while loop as long as number
is greater than 1. Inside the loop, we print out the
number and then we divide it by two, effectively
 halving it. And as expected, the output of the
program is numbers that are progressively getting
halved one after another.

 number = 100
 While (number > 1)
 TextWindow.WriteLine(number)
 number = number / 2
 EndWhile

The do-until selection control
structure
 This is similar to the do-while control but has two
major differences, first the do-until control
structure tests the condition at the end of the
loop. Secondly the structure exits the loop when
the condition is true, i.e. until a condition is met.

Unconditional looping (For loop)
 Unconditional looping are those that carry out a
process a set number of times before it ends. For
example the following code will print out numbers
from 1 to 24 before it stops;
 For i = 1 To 24
 TextWindow.WriteLine(i)
 EndFor

Coding the program
 Program coding is the actual writing of the program to get a
program source code using a specific programming language
once the design has been developed and reviewed.
 Computer programs are written using the specific rules and
statements of the particular computer language being used,
much like grammar rules in the English language. The specific
rule for writing instructions in a particular computer
language is known as syntax. The programmer therefore
must follow the syntax of the language being used.


Arrays
 This object provides a way of storing more than
one value for a given name. These values can be
accessed by another index (key). For example, the
program can store the names of individuals in class
plus their marks, address and age which can be
selected by the index.
 For example, in the code below, data on individuals
of their name, age, and address is accessed using
“person” as the index

 person["Name "] = " Kizito Samuel"
 person["Age "] = 30
 person["Address "] = " Wakiso"
 TextWindow.WriteLine(person)

Variables
A variable is defined as a place in computer memory where you
can store values temporarily and use them later, represented as
a symbol or name associated with a value and whose
associated value may be changed.
Variables can represent numeric values, characters, character
strings, or memory addresses.
Rather than entering data directly into a program, a
programmer can use variables to represent the data. Then,
when the program is executed, the variables are replaced with
real data. This makes it possible for the same program to
process different sets of data.

 Every variable has a name, called the variable
name, and a data type. A variable's data type
indicates what sort of value the variable
represents, such as whether it is an integer or a
character.
 The opposite of a variable is a constant. Constants
are values that never change. Because of their
inflexibility, constants are used less often than
variables in programming.

Using variables: example (small Basic)
 number1 = 10
 number2 = 20
 number3 = number1 * number2
 TextWindow.WriteLine(number3)

 TextWindow.Write("Enter temperature in
Fahrenheit: ")
 fahr = TextWindow.ReadNumber()
 Celsius = 5 * (fahr - 32) / 9
 TextWindow.WriteLine("Temperature in
Celsius is " + Celsius)

Data types used in a programming
language
 Programming languages use three main types of data:
numeric, string (or text) and Boolean variables.
 Numeric variables can store integer or decimal numbers.
They can be positive or negative.
 A string variable is one that stores a string (list) of various
characters. A string can be a name, a string of numbers, a
sentence, a paragraph, any characters at all. And, many
times, a string will contain no characters at all i.e. (). Strings
are always enclosed in quotes (“). Examples of strings: (“I
“
am a Small Basic programmer”) (“012345”), (“Title
Author”)

Control of program flow
 Program flow is controlled by using both
Conditional operators and Logical operators

Conditional operators
 Conditional operators are also known as numerical
comparison operators. Normally they are used to
compare two values to see whether they are equal
or one value is greater or less than the other
value, then the program decides what actions to
take, e.g. whether to execute a program or
terminate the program.

Conditional Operators
Operator Meaning
= Equal to
> More than
< Less Than
>= More than and equal
<= Less than and equal
<> Not Equal to

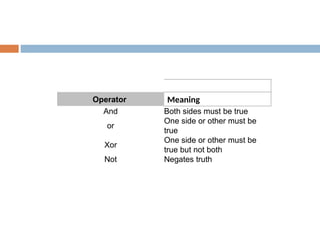
Logical operators
These are operators that allow a program to make a
decision based on multiple conditions. Each operand
is considered a condition that can be evaluated to be
a true or false value. Then the value of the conditions
is used to determine the overall value of the op1
operator op2 or !op1 or both.

Operator Meaning
And Both sides must be true
or
One side or other must be
true
Xor
One side or other must be
true but not both
Not Negates truth

Program testing and debugging
 This involves going through the program to identify
and correct errors. It also involves creating test
data to evaluate if the program generates the
expected output.

Debugger
 A Debugger is special program used to find errors
(bugs) in other programs. A debugger allows a
programmer to stop a program at any point and
examine and change the values of variables.
 debugging involves running the program using test
data to discover and remove any errors in the
program. There are three types of errors: syntax,
logic and runtime errors.

 A syntax error is an error in the grammar of the
programming language. These errors are caused by
typographical errors and incorrect use of the
programming language. They are usually the
easiest bugs to fix.
 A logic error is an error in reasoning, such as the
incorrect sequencing of instructions, and flawed
comparisons and selection statements.

 Runtime errors are errors that occur after the
program has been tested and debugged; they
occur during the execution or running of the
program. One of the reasons these errors can
occur is if the program is stuck in an infinite loop.
Since some computers set limits for how long your
program is allowed to run, a runtime error may
occur if the loop continues up to the time limit
allowed.

Writing instructions
Data input and storage instructions
These instructions accept data that is entered into
the computer and store the value in the location
with the given variable names.
Commands used to input data are READ or INPUT.
Syntax: READ < Variable name>, <Variable name>
Example: READ Name, Score

Prompting instructions
 Prompting statements are used along with input
statements to request or notify the user to enter
data into the computer. These statements are
usually displayed on the screen. Prompting
instructions usually precede input instructions.
 Commands used to prompt the user are PRINT or
WRITE.
 Syntax: PRINT <String>
 Example: PRINT "Enter student name"

Example
Write a program to enter the base and height of a triangle
and find and print the area.
PRINT "Enter the Base"
READ Base
PRINT "Enter the Height"
READ Height
Area = (base*height)/2
Print “area of the triangle is ” + Area + “square cms”

Output Instructions
 These instructions display (or output) the data that is in
the computer’s memory.
 Commands used to output the data are PRINT or
WRITE. You can output string variables and numeric
variables as follows.
 Syntax: PRINT < Variable name >, < Variable name >
 Example:
 PRINT Name, Score
 PRINT Percentage

Outputting a string constant
When a string constant is printed, the exact
characters within the quotation marks are printed.
Syntax: PRINT "String"
Example of variable strings;
PRINT "Opiyo is my name"
PRINT "Time"
PRINT "Sum = 3 + 4"

Outputting a string constant and a
variable
 It may become necessary to output a label for a
variable to identify what is being printed.
 For example, if $4.35 is printed by itself, you may
not know what it means unless a descriptor or
label goes along with it, such as:
 totalCost = $4.35
 Syntax: PRINT “String”, <Variable>
 Example: PRINT “totalCost", + Cost

Comparison/selection/decision
statements
 It sometimes becomes necessary when processing data to
compare the value of a variable to the value of another
variable, or to compare the value of a variable to that of a
constant.
 The following relational operators are used to make such
comparisons.
 A condition is an expression that when evaluated gives either
a TRUE or a FALSE. This expression is called a Boolean
expression. These conditions use the relational operators
between two variables, or between a variable and a constant.


Boolean operators
When selection is based upon one or more
expressions/decisions being TRUE or FALSE, it is
possible to combine the expressions/decisions
together using the Boolean operators AND or OR.
If the AND operator is used, both conditions must
be met in order for the total expression to be true.
If the OR operator is used, either condition must be
met in order for the total expression to be true.

Example
 A club plays football only on Sundays and only if it
is not raining. Read the day and the weather and
print ‘Game on’ if it is a suitable day for playing.

With the AND operator
 Both conditions must be met for the expression to be
true and for ‘Game on’ to be printed. If either condition
is not met, such as the day is not ‘Sunday’ or the
weather is ‘Rain’, then the action (printing ‘Game on’) is
not taken:
 PRINT "Enter the Day and the Weather"
 READ Day, Weather
 IF Day = "Sunday" AND Weather = "No Rain" THEN
 PRINT "Game on"
 ENDIF

With the OR operator
In this case, if either condition is true then the action
is taken. So, if the day is ‘Sunday’, regardless of the
weather, the game is on. If the weather is ‘No Rain’,
regardless of the day, the game is on:
PRINT "Enter the Day and the Weather"
READ Day, Weather
IF Day = "Sunday" OR Weather = "No Rain" THEN
 PRINT "Game on"
ENDIF

The FOR construct
In this construct the loop is controlled by a counter
which increases each time the set of instructions is
executed. This construct is used when the number of
times a set of instructions has to be repeated is known.
 Syntax:
FOR <Variable> = <Beginning value> TO <Ending value>
DO
 <Action to be repeated>
ENDFOR

Example:
 FOR Counter = 1 TO 4 DO
 <Action to be repeated >
 ENDFOR
 When this statement is executed, the counter variable is
initially set to the beginning value, in this case, 1. After
the execution of the instructions between the FOR and
the ENDFOR, the counter variable is increased by 1. The
instructions are repeated and the counter variable
increases until it becomes equal to the ending value, in
this case, 4. So the instructions are repeated four times.

 TextWindow.Title = “wellcome Program"
TextWindow.WriteLine("Welcome to Beginning
Small Basic!")
 A program is made up of many statements. Every
line is a statement and every statement instructs
the computer to do something:

 TextWindow is an object built into Small Basic – it
is the window that displays the output of the
program. Objects have
both properties and methods. Properties describe
objects, while methods do things to objects. In first
single line of code, we are setting the Title property
of the TextWindow object to the text string
“Welcome Program”. The dot (.) and assignment
operator (=) are punctuations that must be placed
appropriately for the computer to understand your
intent.

 This line of code literally says “set
the Title property of the TextWindow object
to Welcome Program.”
 TextWindow.WriteLine("Welcome to Beginning
Small Basic!")
 This line of code uses the
TextWindow WriteLine method to perform the
task. We say the text “Welcome to Beginning Small
Basic!” is passed to the WriteLine method

 The input is placed in parentheses – which
then results in the input text being written in
the text window.

Some basic rules of Small Basic
 All keywords must be spelled correctly.
 To set an object property, we use the following ‘dot’
convention:
ObjectName.PropertyName = PropertyValue
where ObjectName is the
object, PropertyName the property
and PropertyValue the value you want to establish.

 To invoke an object method, use this
convention:
ObjectName.MethodName(MethodInputs)
where ObjectName is the
object, MethodName the method
and MethodInputs the inputs needed by
the method.

 Small Basic has a feature called “intellisense”
that helps you type your programs faster.
When this list appears, you move through the
list using the up/down arrow keys and make a
selection by pressing <Enter>. It will appear
for object names, properties and methods.

 As soon as you type TextWindow, this appears in
the help area of the Small Basic environment:

 Small Basic provides “context-sensitive” help. The help
area will always display information it deems is important
to the user at the appropriate time. In this case,
information concerning the properties (marked by
painter’s palette icon) and methods (marked by gear icon)
for the TextWindow object are displayed. And, once you
select a property or method, a help description for that
selection appears. For example, once you type Title, you
will see this help screen describing the property and how
its used:


Introduction to high level Computer programming

Introduction to high level Computer programming

Recommended

More Related Content

Similar to Introduction to high level Computer programming (20)

Recently uploaded (20)

Introduction to high level Computer programming