KDD2014 勉強会
6 likes•1,629 views
KDD2014勉強会＠北大 KDD2014 Best Paper担当
![伏線：KDDはこういうのに結構関⼼心があるらしい…
[22] KDD09: Efficient methods for topic model inference
on streaming document collections
by Limin Yao, David Mimno, Andrew McCallum (UMass)
KDD08: Fast collapsed gibbs sampling for latent dirichlet
allocation
by Ian Porteous, David Newman, Alex Ihler, Arthur Asuncion,
Padhraic Smyth, Max Welling (UC Irvine)](https://image.slidesharecdn.com/1gacslide-140930033156-phpapp02/85/KDD2014-2-320.jpg)
![準備1：離離散分布とDirichlet分布
離離散分布
※カテゴリカル分布・⼀一般化Bernoulli分布とも
(時々、多項分布と混同して呼ばれるが異異なる分布！)
θ1
θ2
θ3
1 2 3
θ=(θ1,θ2,θ3)
θi := iが出る確率率率
パラメタ
Discrete(θ)
θi ≧ 0, Σi θi =1
“確率率率変数 Z が分布 Discrete(θ) に従う”
Z 〜～ Discrete(θ)
Z の値は 1,2,3 のどれか
with 確率率率 P(Z=i) = θi
Discrete(θ)からZをサンプリングすると
確率率率θに従って{1,2,3}のいずれかを得る。
Beta分布
[0,1]の間の実数の⾮非⼀一様乱数が欲しい！
http://www.ntrand.com/images/functions/plot/plotBeta.jpg
※ こういう⾵風に変化する分布族を設計するのは
「意外に」メンドイ (ベータ関数・ガンマ関数)](https://image.slidesharecdn.com/1gacslide-140930033156-phpapp02/85/KDD2014-14-320.jpg)
![準備1：離離散分布とDirichlet分布
離離散分布
※カテゴリカル分布・⼀一般化Bernoulli分布とも
(時々、多項分布と混同して呼ばれるが異異なる分布！)
θ1
θ2
θ3
1 2 3
θ=(θ1,θ2,θ3)
θi := iが出る確率率率
パラメタ
Discrete(θ)
θi ≧ 0, Σi θi =1
“確率率率変数 Z が分布 Discrete(θ) に従う”
Z 〜～ Discrete(θ)
Z の値は 1,2,3 のどれか
with 確率率率 P(Z=i) = θi
Discrete(θ)からZをサンプリングすると
確率率率θに従って{1,2,3}のいずれかを得る。
Beta分布
[0,1]の間の実数の⾮非⼀一様乱数が欲しい！
http://www.ntrand.com/images/functions/plot/plotBeta.jpg
※ こういう⾵風に変化する分布族を設計するのは
「意外に」メンドイ (ベータ関数・ガンマ関数)
[0,1]の⾮非⼀一様乱数をN個つくって、さらに
N個とも⾜足したら常に1になるようにしたい？
→ Dirichlet分布 登場！](https://image.slidesharecdn.com/1gacslide-140930033156-phpapp02/85/KDD2014-15-320.jpg)
![準備2：Walkerʼ’s alias method (1974)
問題：コレ↓どうやって実装する？？
離離散分布 k=5
1 2 3 4 5
1,5,5,3,5,4,5,5,3,1,…
乱数⽣生成
サンプル
1 2 3 4 5
a b c d
0 1
⼀一様乱数
u ← [0,1]の⼀一様乱数
if u < a
return 1
else if u < b
return 2
else if u < c
return 3
else if u < d
return 4
else
return 5
u
右のようにやって O(k)
※⼆二分探索索すると O(log k)](https://image.slidesharecdn.com/1gacslide-140930033156-phpapp02/85/KDD2014-18-320.jpg)
![準備2：Walkerʼ’s alias method (1974)
問題：コレ↓どうやって実装する？？
離離散分布 k=5
1 2 3 4 5
1,5,5,3,5,4,5,5,3,1,…
乱数⽣生成
サンプル
1 2 3 4 5
a b c d
0 1
⼀一様乱数
u ← [0,1]の⼀一様乱数
if u < a
return 1
else if u < b
return 2
else if u < c
return 3
else if u < d
return 4
else
return 5
u
右のようにやって O(k)
※⼆二分探索索すると O(log k)
ちょっとした前処理理をするとこれをO(1)で出来る (Walkerʼ’s alias method)
GNU Rはver 2.2.0で復復元抽出に採⽤用](https://image.slidesharecdn.com/1gacslide-140930033156-phpapp02/85/KDD2014-19-320.jpg)
![準備2：Walkerʼ’s alias method (1974)
問題：コレ↓どうやって実装する？？
離離散分布 k=5
1 2 3 4 5
1,5,5,3,5,4,5,5,3,1,…
乱数⽣生成
サンプル
1 2 3 4 5
a b c d
0 1
⼀一様乱数
u ← [0,1]の⼀一様乱数
if u < a
return 1
else if u < b
return 2
else if u < c
return 3
else if u < d
return 4
else
return 5
u
右のようにやって O(k)
※⼆二分探索索すると O(log k)
ちょっとした前処理理をするとこれをO(1)で出来る (Walkerʼ’s alias method)
GNU Rはver 2.2.0で復復元抽出に採⽤用
ポイント１：もし上の分割が等分割なら、O(1)で出来ることを思い出す
例例） 「rand()%6」は0から5の整数の乱数
ポイント２：前処理理で”等分割+1回の⼆二者択⼀一”で⾏行行けるようTableを整理理(Alias Table)
1 2 3 4 5
0 1
A B C D E A: u<a→1 else 3
0 1
B: u<b→2 else 3
a b c d :](https://image.slidesharecdn.com/1gacslide-140930033156-phpapp02/85/KDD2014-20-320.jpg)
![寄り道：Rejection Sampling 2/2
p(x)>0 ⇒ q(x)>0 かつ p(x)/q(x)≦c となる定数cが存在するような
分布qが提案分布ならば、以下の出⼒力力xは分布pからのサンプリング
i) y ← qからのサンプル, u ← [0,1]の⼀一様乱数
ii) If u ≦ 1/c × p(y)/q(y)、x ← y (提案yを受理理)
Else i)に戻る
※ q(x)は条件を満たせば何でも良良いが、p(x)とq(x)が違いすぎると
受理理される確率率率が下がり、無駄なサンプリングが増えるので効率率率悪
＋ 定数cが存在しないか計算するのにコストがかかる場合も多い
参考) なぜこれでpからのサンプリングができるのか？→ cdfをcheck!](https://image.slidesharecdn.com/1gacslide-140930033156-phpapp02/85/KDD2014-52-320.jpg)
![MCMC(2) Metropolis-‐‑‒Hastings Sampling
⽬目的：⽬目標分布pからxをサンプリング
Gibbs Samplingの制約：各条件付き分布からサンプリングができる場合に限る
→ サンプリングしやすい別の分布q(y|x)を⽤用いて提案yを⽣生成し受理理/棄却
i) , ← [0,1]の⼀一様乱数
ii) If then
Else
(提案を受理理)
(提案を棄却)
【驚くべき性質】提案分布q(y|x)はほぼ任意!! (独⽴立立q(y)とか、Gaussで乱歩とか)
ただし、分布q(y|x)が真の分布p(y)から遠いと無駄が多くなり効率率率は下がる
(Gibbsは100%受理理されるMetropolis-‐‑‒Hastingsの⼀一種と⾒見見る事もできる)](https://image.slidesharecdn.com/1gacslide-140930033156-phpapp02/85/KDD2014-54-320.jpg)
![従来の知⾒見見 2/2
LDAのCollapsed Gibbs Sampling
⽂文献[22]：上の右辺を以下のように分解して⼯工夫すると に!
Sparse Sparse Dense
ここがゼロになりやすい
単語wが含む
トピック数
⽂文書dが含む
トピック数
は⽂文書数(⼩小)なら確かに
で結局 に、、、
でも⽂文書数(⼤大)になると
⽂文献[22]の結果の問題](https://image.slidesharecdn.com/1gacslide-140930033156-phpapp02/85/KDD2014-59-320.jpg)
![本論論⽂文の内容 1/4
は⽂文書数(⼩小)なら確かに
で結局 に、、、
でも⽂文書数(⼤大)になると
以下の分解により に改善！ ⽂文書dが含むトピック数
単語wに割当られたトピック数
Sparse Dense
⽂文献[22]の結果の問題
第１項、第２項のみに⽐比例例
する⼆二つの離離散分布を考える
離離散分布１ 離離散分布２
正規化項(Σk右辺)を正規化項(Σk右辺)を](https://image.slidesharecdn.com/1gacslide-140930033156-phpapp02/85/KDD2014-60-320.jpg)
![本論論⽂文の内容 3/4
この２つの分布のmixtureを提案分布にしてMetropolis-‐‑‒Hasting Sampling
sparseな項なので
exactにサンプリング
denseな項なので
Alias methodでO(1)で取る
(なので実際はちょっと前の分布)
MHの原理理により以下で得るxは⽬目標分布からのサンプル
i) 確率率率で から、確率率率 で から y をサンプリング
ii) [0,1]の⼀一様乱数 u が「u ≦ min(1,π)」を満たす場合に y を x として受理理
正規化項が
キャンセル!](https://image.slidesharecdn.com/1gacslide-140930033156-phpapp02/85/KDD2014-62-320.jpg)
KDD2014 勉強会
- 1. 紹介する論論⽂文： Reducing the Sampling Complexity of Topic Models (KDD2014 Best Paper) Aaron Q Li (CMU) Amr Ahmed (Google) Sujith Ravi (Google) Alexander J Smola (CMU & Google) 担当：瀧川 ⼀一学
- 2. 伏線：KDDはこういうのに結構関⼼心があるらしい… [22] KDD09: Efficient methods for topic model inference on streaming document collections by Limin Yao, David Mimno, Andrew McCallum (UMass) KDD08: Fast collapsed gibbs sampling for latent dirichlet allocation by Ian Porteous, David Newman, Alex Ihler, Arthur Asuncion, Padhraic Smyth, Max Welling (UC Irvine)
- 3. 要点: トピックモデルの推定に使うサンプリングを速くする話 • トピックモデルを普通にCollapsed Gibbs Samplingで 推定する際に隠れ変数のサンプリングを⾏行行うが、普通は コーパス全体が含むトピック数のオーダかかってしまう。 • これを各ドキュメントが実際に含むトピック数のオーダ に落落とす話 • 道具その１：Walkerʼ’s Alias Method • 道具その２：Metropolis-‐‑‒Hastings Sampling
- 4. 論論⽂文を読むのに必要となる知識識 (⾚赤字部を今⽇日解説します) • トピックモデルとサンプリング(乱数⽣生成)によるBayes推定 LDA (Latent Dirichlet Allocation) LDAのノンパラ拡張： Poisson-‐‑‒Dirichlet Process (PDP) Hierarchical Dirichlet Process (HDP) • 乱数⽣生成１ Walkerʼ’s Alias Method (Walkerの別名法 aka ⼆二者択⼀一法) Rejection Sampling • 乱数⽣生成２：MCMC (Markov Chain Monte Carlo) (Collapsed) Gibbs Sampling Metropolis-‐‑‒Hastings Sampling 論論⽂文の⽅方法はLDA,PDP,HDPに共通なので、今回はLDAに絞って 上の事項の知識識を全く仮定せずに要点を説明してみます！
- 5. 論論旨の直感的なsneak peek サンプリング • 標本抽出 = ある分布に従う乱数⽣生成
- 6. 論論旨の直感的なsneak peek サンプリング • 標本抽出 = ある分布に従う乱数⽣生成 トピック分布 1 2 3 4 5 6 7 8 乱数⽣生成 各語のトピックアロケーション 2, 4, 7, 7, 2, 8, 2, 4, … • LDAのGibbs Samplingでの推定はただ離離散分布からのサンプリングを 繰返せば良良いだけ(!)になる。(ただし分布が毎度度変わる)
- 7. 論論旨の直感的なsneak peek サンプリング • 標本抽出 = ある分布に従う乱数⽣生成 トピック分布 1 2 3 4 5 6 7 8 乱数⽣生成 各語のトピックアロケーション 2, 4, 7, 7, 2, 8, 2, 4, … • LDAのGibbs Samplingでの推定はただ離離散分布からのサンプリングを 繰返せば良良いだけ(!)になる。(ただし分布が毎度度変わる) • 離離散分布からのサンプリングは(前処理理すれば) O(1)で⾏行行う⽅方法が！ → Walkerʼ’s alias method
- 8. 論論旨の直感的なsneak peek サンプリング • 標本抽出 = ある分布に従う乱数⽣生成 トピック分布 1 2 3 4 5 6 7 8 乱数⽣生成 各語のトピックアロケーション 2, 4, 7, 7, 2, 8, 2, 4, … • LDAのGibbs Samplingでの推定はただ離離散分布からのサンプリングを 繰返せば良良いだけ(!)になる。(ただし分布が毎度度変わる) • 離離散分布からのサンプリングは(前処理理すれば) O(1)で⾏行行う⽅方法が！ → Walkerʼ’s alias method • ただ、LDAのGibbs Samplingの状況では分布が変わるので使えない。 …んですが、分布変わるとは⾔言え普通はそんなに⼤大きくは変わらない。
- 9. 論論旨の直感的なsneak peek サンプリング • 標本抽出 = ある分布に従う乱数⽣生成 トピック分布 1 2 3 4 5 6 7 8 乱数⽣生成 各語のトピックアロケーション 2, 4, 7, 7, 2, 8, 2, 4, … • LDAのGibbs Samplingでの推定はただ離離散分布からのサンプリングを 繰返せば良良いだけ(!)になる。(ただし分布が毎度度変わる) • 離離散分布からのサンプリングは(前処理理すれば) O(1)で⾏行行う⽅方法が！ → Walkerʼ’s alias method • ただ、LDAのGibbs Samplingの状況では分布が変わるので使えない。 …んですが、分布変わるとは⾔言え普通はそんなに⼤大きくは変わらない。 • そこでGibbsを⽌止めてMetropolis-‐‑‒Hasting(MH)にする。 MHの提案分布(の⼀一部)をAlias methodからO(1)で取れる古いサンプル で作り、真の⽬目標分布とのズレはMHのAccept/Rejectステップで補正
- 10. 論論旨の直感的なsneak peek サンプリング • 標本抽出 = ある分布に従う乱数⽣生成 トピック分布 1 2 3 4 5 6 7 8 乱数⽣生成 各語のトピックアロケーション 2, 4, 7, 7, 2, 8, 2, 4, … • LDAのGibbs Samplingでの推定はただ離離散分布からのサンプリングを 繰返せば良良いだけ(!)になる。(ただし分布が毎度度変わる) • 離離散分布からのサンプリングは(前処理理すれば) O(1)で⾏行行う⽅方法が！ → Walkerʼ’s alias method • ただ、LDAのGibbs Samplingの状況では分布が変わるので使えない。 …んですが、分布変わるとは⾔言え普通はそんなに⼤大きくは変わらない。 • そこでGibbsを⽌止めてMetropolis-‐‑‒Hasting(MH)にする。 MHの提案分布(の⼀一部)をAlias methodからO(1)で取れる古いサンプル で作り、真の⽬目標分布とのズレはMHのAccept/Rejectステップで補正 • 提案分布 = ”疎な部分”+”密な部分”のmixture (後者を古いサンプルで)
- 11. 本⽇日の発表の流流れ ← イマココ 1. 全体概要と前説 2. 準備1：離離散分布とDirichlet分布 3. 準備2：Walkerʼ’s alias method (1974) 離離散分布からの復復元抽出をO(1)でやる⽅方法 4. トピックモデル/⽣生成モデル概観 何がしたいのか & どうやって求めるのか 5. ベイズ推定とLatent Dirichlet Allocation(LDA) 6. MCMC概観 Gibbs Sampling vs Metropolis-‐‑‒Hastings Sampling (non MCMCなRejection Samplingとの関係を横⽬目で⾒見見つつ) 7. 本論論⽂文の紹介：分布の疎密分解+Alias method+MH step
- 12. 本⽇日の発表の流流れ 1. 全体概要と前説 2. 準備1：離離散分布とDirichlet分布 3. 準備2：Walkerʼ’s alias method (1974) 離離散分布からの復復元抽出をO(1)でやる⽅方法 4. トピックモデル/⽣生成モデル概観 何がしたいのか & どうやって求めるのか 5. ベイズ推定とLatent Dirichlet Allocation(LDA) 6. MCMC概観 Gibbs Sampling vs Metropolis-‐‑‒Hastings Sampling (non MCMCなRejection Samplingとの関係を横⽬目で⾒見見つつ) 7. 本論論⽂文の紹介：分布の疎密分解+Alias method+MH step
- 13. 準備1：離離散分布とDirichlet分布 離離散分布 ※カテゴリカル分布・⼀一般化Bernoulli分布とも (時々、多項分布と混同して呼ばれるが異異なる分布！) θ1 θ2 θ3 1 2 3 θ=(θ1,θ2,θ3) θi := iが出る確率率率 パラメタ Discrete(θ) θi ≧ 0, Σi θi =1 “確率率率変数 Z が分布 Discrete(θ) に従う” Z 〜～ Discrete(θ) Z の値は 1,2,3 のどれか with 確率率率 P(Z=i) = θi Discrete(θ)からZをサンプリングすると 確率率率θに従って{1,2,3}のいずれかを得る。
- 14. 準備1：離離散分布とDirichlet分布 離離散分布 ※カテゴリカル分布・⼀一般化Bernoulli分布とも (時々、多項分布と混同して呼ばれるが異異なる分布！) θ1 θ2 θ3 1 2 3 θ=(θ1,θ2,θ3) θi := iが出る確率率率 パラメタ Discrete(θ) θi ≧ 0, Σi θi =1 “確率率率変数 Z が分布 Discrete(θ) に従う” Z 〜～ Discrete(θ) Z の値は 1,2,3 のどれか with 確率率率 P(Z=i) = θi Discrete(θ)からZをサンプリングすると 確率率率θに従って{1,2,3}のいずれかを得る。 Beta分布 [0,1]の間の実数の⾮非⼀一様乱数が欲しい！ http://www.ntrand.com/images/functions/plot/plotBeta.jpg ※ こういう⾵風に変化する分布族を設計するのは 「意外に」メンドイ (ベータ関数・ガンマ関数)
- 15. 準備1：離離散分布とDirichlet分布 離離散分布 ※カテゴリカル分布・⼀一般化Bernoulli分布とも (時々、多項分布と混同して呼ばれるが異異なる分布！) θ1 θ2 θ3 1 2 3 θ=(θ1,θ2,θ3) θi := iが出る確率率率 パラメタ Discrete(θ) θi ≧ 0, Σi θi =1 “確率率率変数 Z が分布 Discrete(θ) に従う” Z 〜～ Discrete(θ) Z の値は 1,2,3 のどれか with 確率率率 P(Z=i) = θi Discrete(θ)からZをサンプリングすると 確率率率θに従って{1,2,3}のいずれかを得る。 Beta分布 [0,1]の間の実数の⾮非⼀一様乱数が欲しい！ http://www.ntrand.com/images/functions/plot/plotBeta.jpg ※ こういう⾵風に変化する分布族を設計するのは 「意外に」メンドイ (ベータ関数・ガンマ関数) [0,1]の⾮非⼀一様乱数をN個つくって、さらに N個とも⾜足したら常に1になるようにしたい？ → Dirichlet分布 登場！
- 16. 準備1：離離散分布とDirichlet分布 離離散分布Dirichlet分布 ※カテゴリカル分布・⼀一般化Bernoulli分布とも (時々、多項分布と混同して呼ばれるが異異なる分布！) θ1 θ2 θ3 1 2 3 θ=(θ1,θ2,θ3) θi := iが出る確率率率 パラメタ Discrete(θ) θi ≧ 0, Σi θi =1 “確率率率変数 Z が分布 Discrete(θ) に従う” Z 〜～ Discrete(θ) Z の値は 1,2,3 のどれか with 確率率率 P(Z=i) = θi Discrete(θ)からZをサンプリングすると 確率率率θに従って{1,2,3}のいずれかを得る。 ※ベータ分布を多次元版にしたもののひとつ。 周辺分布はベータ分布。 “確率率率変数 θ が分布 Dir(α) に従う” θ:=(θ1,θ2,θ3) 〜～ Dir(α) 単体{θ: θi ≧ 0, Σi θi =1} 上の確率率率分布 θ1 θ2 θ3 1 1 1 分布形状はパラメタ α=(α1,α2,α3) で変化 http://suhasmathur.com/2014/01/dirichlet-and-friends/ Dir(α)からθ=(θ1,θ2,θ3)をサンプリング すると「θi ≧ 0, Σi θi =1」となる。
- 17. 準備2：Walkerʼ’s alias method (1974) 問題：コレ↓どうやって実装する？？ 離離散分布 k=5 1 2 3 4 5 1,5,5,3,5,4,5,5,3,1,… 乱数⽣生成 サンプル
- 18. 準備2：Walkerʼ’s alias method (1974) 問題：コレ↓どうやって実装する？？ 離離散分布 k=5 1 2 3 4 5 1,5,5,3,5,4,5,5,3,1,… 乱数⽣生成 サンプル 1 2 3 4 5 a b c d 0 1 ⼀一様乱数 u ← [0,1]の⼀一様乱数 if u < a return 1 else if u < b return 2 else if u < c return 3 else if u < d return 4 else return 5 u 右のようにやって O(k) ※⼆二分探索索すると O(log k)
- 19. 準備2：Walkerʼ’s alias method (1974) 問題：コレ↓どうやって実装する？？ 離離散分布 k=5 1 2 3 4 5 1,5,5,3,5,4,5,5,3,1,… 乱数⽣生成 サンプル 1 2 3 4 5 a b c d 0 1 ⼀一様乱数 u ← [0,1]の⼀一様乱数 if u < a return 1 else if u < b return 2 else if u < c return 3 else if u < d return 4 else return 5 u 右のようにやって O(k) ※⼆二分探索索すると O(log k) ちょっとした前処理理をするとこれをO(1)で出来る (Walkerʼ’s alias method) GNU Rはver 2.2.0で復復元抽出に採⽤用
- 20. 準備2：Walkerʼ’s alias method (1974) 問題：コレ↓どうやって実装する？？ 離離散分布 k=5 1 2 3 4 5 1,5,5,3,5,4,5,5,3,1,… 乱数⽣生成 サンプル 1 2 3 4 5 a b c d 0 1 ⼀一様乱数 u ← [0,1]の⼀一様乱数 if u < a return 1 else if u < b return 2 else if u < c return 3 else if u < d return 4 else return 5 u 右のようにやって O(k) ※⼆二分探索索すると O(log k) ちょっとした前処理理をするとこれをO(1)で出来る (Walkerʼ’s alias method) GNU Rはver 2.2.0で復復元抽出に採⽤用 ポイント１：もし上の分割が等分割なら、O(1)で出来ることを思い出す 例例） 「rand()%6」は0から5の整数の乱数 ポイント２：前処理理で”等分割+1回の⼆二者択⼀一”で⾏行行けるようTableを整理理(Alias Table) 1 2 3 4 5 0 1 A B C D E A: u<a→1 else 3 0 1 B: u<b→2 else 3 a b c d :
- 21. 本⽇日の発表の流流れ 1. 全体概要と前説 2. 準備1：離離散分布とDirichlet分布 3. 準備2：Walkerʼ’s alias method (1974) 離離散分布からの復復元抽出をO(1)でやる⽅方法 4. トピックモデル/⽣生成モデルのベイズ推定 何がしたいのか & どうやって求めるのか 5. Latent Dirichlet Allocation(LDA) 6. MCMC (Markov Chain Monte Carlo) Gibbs Sampling vs Metropolis-‐‑‒Hastings Sampling (non-‐‑‒MCMCなRejection Samplingとの関係を横⽬目で⾒見見つつ) 7. 本論論⽂文の紹介：分布の疎密分解+Alias method+MH step
- 22. 本⽇日の発表の流流れ 1. 全体概要と前説 2. 準備1：離離散分布とDirichlet分布 3. 準備2：Walkerʼ’s alias method (1974) 離離散分布からの復復元抽出をO(1)でやる⽅方法 4. トピックモデル/⽣生成モデルのベイズ推定 何がしたいのか & どうやって求めるのか 5. Latent Dirichlet Allocation(LDA) 6. MCMC (Markov Chain Monte Carlo) Gibbs Sampling vs Metropolis-‐‑‒Hastings Sampling (non-‐‑‒MCMCなRejection Samplingとの関係を横⽬目で⾒見見つつ) 7. 本論論⽂文の紹介：分布の疎密分解+Alias method+MH step
- 23. トピックモデルとは？ 例例: 以下の３つのニュースヘッダの内容類似度度を測りたい (仕分けや推薦) ❶「逸ノ城、⽩白鵬に敗れ新⼊入幕Ｖ後退 秋場所14⽇日⽬目」 ❷「遠藤、泥泥沼６連敗 全勝の３⼈人は安泰」 ❸「オリックス ドタバタＭ消滅 残り全戦敵地…Ｖロード試練」
- 24. トピックモデルとは？ 例例: 以下の３つのニュースヘッダの内容類似度度を測りたい (仕分けや推薦) ❶「逸ノ城、⽩白鵬に敗れ新⼊入幕Ｖ後退 秋場所14⽇日⽬目」 ❷「遠藤、泥泥沼６連敗 全勝の３⼈人は安泰」 ❸「オリックス ドタバタＭ消滅 残り全戦敵地…Ｖロード試練」 ⾃自然⾔言語処理理では「⽂文書:=bag of words」として⾊色々⾏行行うことが多い。 (通常、助詞や冠詞などの多頻出で無意味なstop wordsも前処理理で除く) ⽂文書1 = {逸ノ城, ⽩白鵬, 敗れ, 新⼊入幕, Ｖ, 後退, 秋場所, 14,⽇日⽬目} ⽂文書2 = {遠藤, 泥泥沼, ６, 連敗, 全勝, ３, ⼈人, 安泰} ⽂文書3 = {オリックス,ドタバタ,Ｍ消滅, 残り,全戦,敵地,Ｖロード,試練}
- 25. トピックモデルとは？ 例例: 以下の３つのニュースヘッダの内容類似度度を測りたい (仕分けや推薦) ❶「逸ノ城、⽩白鵬に敗れ新⼊入幕Ｖ後退 秋場所14⽇日⽬目」 ❷「遠藤、泥泥沼６連敗 全勝の３⼈人は安泰」 ❸「オリックス ドタバタＭ消滅 残り全戦敵地…Ｖロード試練」 ⾃自然⾔言語処理理では「⽂文書:=bag of words」として⾊色々⾏行行うことが多い。 (通常、助詞や冠詞などの多頻出で無意味なstop wordsも前処理理で除く) ⽂文書1 = {逸ノ城, ⽩白鵬, 敗れ, 新⼊入幕, Ｖ, 後退, 秋場所, 14,⽇日⽬目} ⽂文書2 = {遠藤, 泥泥沼, ６, 連敗, 全勝, ３, ⼈人, 安泰} ⽂文書3 = {オリックス,ドタバタ,Ｍ消滅, 残り,全戦,敵地,Ｖロード,試練} 問題「げ、共通の単語がねえ…」 ⽂文書の特徴ベクトル = (単語1の頻度度、単語2の頻度度、…)みたいのでは×
- 26. トピックモデルとは？ ⽂文書1 = {逸ノ城, ⽩白鵬, 敗れ, 新⼊入幕, Ｖ, 後退, 秋場所, 14, ⽇日⽬目} ⽂文書2 = {遠藤, 泥泥沼, ６, 連敗, 全勝, ３, ⼈人, 安泰} ⽂文書3 = {オリックス,ドタバタ,Ｍ消滅, 残り,全戦,敵地,Ｖロード,試練} しかし、⽂文書1と2は相撲の話、⽂文書3は野球の話。1と2が似てることが 分かるのは内容のトピックが似ているから。 つまり、⽂文書をそれが含むトピックによって特徴付けた⽅方が良良さそう！
- 27. トピックモデルとは？ ⽂文書1 = {逸ノ城, ⽩白鵬, 敗れ, 新⼊入幕, Ｖ, 後退, 秋場所, 14, ⽇日⽬目} ⽂文書2 = {遠藤, 泥泥沼, ６, 連敗, 全勝, ３, ⼈人, 安泰} ⽂文書3 = {オリックス,ドタバタ,Ｍ消滅, 残り,全戦,敵地,Ｖロード,試練} しかし、⽂文書1と2は相撲の話、⽂文書3は野球の話。1と2が似てることが 分かるのは内容のトピックが似ているから。 つまり、⽂文書をそれが含むトピックによって特徴付けた⽅方が良良さそう！ とりあえず、各単語にトピックを割り当て(allocate)してみる。
- 28. トピックモデルとは？ ⽂文書1 = {逸ノ城, ⽩白鵬, 敗れ, 新⼊入幕, Ｖ, 後退, 秋場所, 14, ⽇日⽬目} ⽂文書2 = {遠藤, 泥泥沼, ６, 連敗, 全勝, ３, ⼈人, 安泰} ⽂文書3 = {オリックス,ドタバタ,Ｍ消滅, 残り,全戦,敵地,Ｖロード,試練} しかし、⽂文書1と2は相撲の話、⽂文書3は野球の話。1と2が似てることが 分かるのは内容のトピックが似ているから。 つまり、⽂文書をそれが含むトピックによって特徴付けた⽅方が良良さそう！ とりあえず、各単語にトピックを割り当て(allocate)してみる。 逸ノ城→”相撲” ⽩白鵬→”相撲” 遠藤→ …、あれ？遠藤は相撲のですか、 サッカーのですか、他のスポーツにも居るかもですよね…。
- 30. ⽣生成モデルとベイズ推定 単語のトピックへのallocationは”確率率率的に”考えるのが良良さそう そこで⽂文書をトピックを通じて確率率率的に⽣生成するモデルを⽴立立てる ⽣生成モデル：Zはトピック1〜～kのどれかを取る確率率率変数とすると、 トピックZと単語wの同時確率率率 p(w,Z) を「陽に」モデル化すれば良良い。
- 31. ⽣生成モデルとベイズ推定 単語のトピックへのallocationは”確率率率的に”考えるのが良良さそう そこで⽂文書をトピックを通じて確率率率的に⽣生成するモデルを⽴立立てる ⽣生成モデル：Zはトピック1〜～kのどれかを取る確率率率変数とすると、 トピックZと単語wの同時確率率率 p(w,Z) を「陽に」モデル化すれば良良い。 →各⽂文書(bag of words)とはこういうステップで確率率率的にできますよー という⽣生成の過程のモデルをなんちゃら分布とかで勝⼿手に決める。
- 32. ⽣生成モデルとベイズ推定 単語のトピックへのallocationは”確率率率的に”考えるのが良良さそう そこで⽂文書をトピックを通じて確率率率的に⽣生成するモデルを⽴立立てる ⽣生成モデル：Zはトピック1〜～kのどれかを取る確率率率変数とすると、 トピックZと単語wの同時確率率率 p(w,Z) を「陽に」モデル化すれば良良い。 →各⽂文書(bag of words)とはこういうステップで確率率率的にできますよー という⽣生成の過程のモデルをなんちゃら分布とかで勝⼿手に決める。 モデルの推定：⼿手元にある実際の⽂文書たちが本当にそのモデルから出たと仮定して ⼀一番もっともらしいモデルの未知部分を計算する作業。例例えばZは観測されないので ⼿手元の情報から各Zの値が1〜～kのどれっぽいかの確率率率分布 p(Z|w) を求めたい。
- 33. ⽣生成モデルとベイズ推定 単語のトピックへのallocationは”確率率率的に”考えるのが良良さそう そこで⽂文書をトピックを通じて確率率率的に⽣生成するモデルを⽴立立てる ⽣生成モデル：Zはトピック1〜～kのどれかを取る確率率率変数とすると、 トピックZと単語wの同時確率率率 p(w,Z) を「陽に」モデル化すれば良良い。 →各⽂文書(bag of words)とはこういうステップで確率率率的にできますよー という⽣生成の過程のモデルをなんちゃら分布とかで勝⼿手に決める。 モデルの推定：⼿手元にある実際の⽂文書たちが本当にそのモデルから出たと仮定して ⼀一番もっともらしいモデルの未知部分を計算する作業。例例えばZは観測されないので ⼿手元の情報から各Zの値が1〜～kのどれっぽいかの確率率率分布 p(Z|w) を求めたい。 (隠れ変数モデル) 観測されない変数Zの分布をベイズ則 p(Z|w) = p(w,Z)/p(w) = p(w|Z)p(Z)/p(w) で、⼿手元の情報〜～モデル(既知)と観測w〜～で表現できる形に書き換える。
- 34. Latent Dirichlet Allocation (LDA) の⽣生成モデル
- 35. Latent Dirichlet Allocation (LDA) の⽣生成モデル 各⽂文書dに対して各トピックkに対して 各単語 i に対して 調整パラメタ調整パラメタ トピックkの単語分布 ⽂文書dのトピック分布 ⽂文書dの 単語 i の トピック割当 ⽂文書dの単語 i (given) (given) (given) トピック数 K, 出現単語数 W, ⽂文書数 Dとする。
- 36. Latent Dirichlet Allocation (LDA) の⽣生成モデル 各⽂文書dに対して各トピックkに対して 各単語 i に対して 調整パラメタ調整パラメタ トピックkの単語分布 ⽂文書dのトピック分布 ⽂文書dの 単語 i の トピック割当 ⽂文書dの単語 i (given) (given) (given) トピック数 K, 出現単語数 W, ⽂文書数 Dとする。 ❶ トピック1 単語W 単語1 単語2 … 単語3 単語W-‐‑‒1 K個 ❶
- 37. Latent Dirichlet Allocation (LDA) の⽣生成モデル 各⽂文書dに対して各トピックkに対して 各単語 i に対して 調整パラメタ調整パラメタ トピックkの単語分布 ⽂文書dのトピック分布 ⽂文書dの 単語 i の トピック割当 ⽂文書dの単語 i (given) (given) (given) トピック数 K, 出現単語数 W, ⽂文書数 Dとする。 ❶ トピック1 単語W 単語1 単語2 … 単語3 単語W-‐‑‒1 ⽂文書d トピックK トピック1 … トピック2 トピックK-‐‑‒1 ❷ K個 ❷
- 38. Latent Dirichlet Allocation (LDA) の⽣生成モデル 各⽂文書dに対して各トピックkに対して 各単語 i に対して 調整パラメタ調整パラメタ トピックkの単語分布 ⽂文書dのトピック分布 ⽂文書dの 単語 i の トピック割当 ⽂文書dの単語 i (given) (given) (given) トピック数 K, 出現単語数 W, ⽂文書数 Dとする。 ❶ トピック1 単語W 単語1 単語2 … 単語3 単語W-‐‑‒1 ⽂文書d トピックK トピック1 … トピック2 トピックK-‐‑‒1 ❷ K個 ❸ トピックK トピック1 … トピック2 トピックK-‐‑‒1 ❸
- 39. Latent Dirichlet Allocation (LDA) の⽣生成モデル 各⽂文書dに対して各トピックkに対して 各単語 i に対して 調整パラメタ調整パラメタ トピックkの単語分布 ⽂文書dのトピック分布 ⽂文書dの 単語 i の トピック割当 ⽂文書dの単語 i (given) (given) (given) トピック数 K, 出現単語数 W, ⽂文書数 Dとする。 ❶ トピック1 単語W 単語1 単語2 … 単語3 単語W-‐‑‒1 ⽂文書d トピックK トピック1 … トピック2 トピックK-‐‑‒1 ❷ K個 ❸ トピックK トピック1 … トピック2 トピックK-‐‑‒1 ❹ トピック zdi 単語W 単語1 単語2 … 単語3 単語W-‐‑‒1 × dの 単語数 ❹
- 40. Latent Dirichlet Allocation (LDA) の⽣生成モデル 各⽂文書dに対して各トピックkに対して 各単語 i に対して 調整パラメタ調整パラメタ トピックkの単語分布 ⽂文書dのトピック分布 ⽂文書dの 単語 i の トピック割当 ⽂文書dの単語 i (given) (given) (given) トピック数 K, 出現単語数 W, ⽂文書数 Dとする。 ❶ トピック1 単語W 単語1 単語2 … 単語3 単語W-‐‑‒1 ⽂文書d トピックK トピック1 … トピック2 トピックK-‐‑‒1 ❷ K個D個 ❸ トピックK トピック1 … トピック2 トピックK-‐‑‒1 ❹ トピック zdi 単語W 単語1 単語2 … 単語3 単語W-‐‑‒1 × dの 単語数
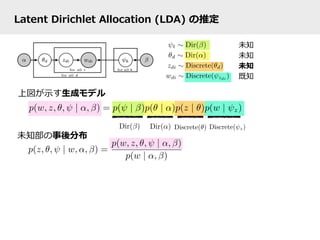
- 41. Latent Dirichlet Allocation (LDA) の推定 上図が⽰示す⽣生成モデル 未知部の事後分布 未知 未知 未知 既知
- 42. Latent Dirichlet Allocation (LDA) の推定 上図が⽰示す⽣生成モデル 未知部の事後分布 “collapsed” … θとψを積分消去 (DirとDiscreteが共役なので) zdi 以外の全ての zj 未知 未知 未知 既知
- 43. Latent Dirichlet Allocation (LDA) の推定 上図が⽰示す⽣生成モデル 未知部の事後分布 z: ⼗十分統計量量 “collapsed” … θとψを積分消去 (DirとDiscreteが共役なので) zdi 以外の全ての zj 未知 未知 未知 既知 zから計算 できる (Dirichlet 平滑滑化の形)
- 44. LDAのCollapsed Gibbs Samplerの条件付き分布 ⽣生成モデルをcollapse 共役な対ごとに計算
- 45. LDAのCollapsed Gibbs Samplerの条件付き分布 ⽣生成モデルをcollapse 共役な対ごとに計算 こんな感じで を整理理していくと… … 論論⽂文の(5)式 注意：「・-‐‑‒di」はdiを除いたカウントの意味(-‐‑‒di乗ではない) 従って、zdi=k となる確率率率は右辺で計算され (単に離離散分布)、しかも後述のMCMCの 理理屈によって、「zdi を右辺の離離散分布から実際にサンプリング」を繰返すだけでOK(!)
- 46. 結局、LDAは何をやっているの？？ 基底分解 bag of words(単語頻度度分布) ⽂文書1 ⽂文書2 … ⽂文書D 単語1 単語2 単語W … 0 7 2 1 0 0 … … … 0 2 5 ⽂文書1 ⽂文書2 … ⽂文書D トピック1 トピック2 トピックK … … 単語1 単語2 単語W … … トピック1 トピック2 トピックK … 各⽂文書のトピック分布 コーパス 各トピックの単語頻度度分布 トピック空間での 低次元表現 単語の(ソフト) クラスタリング (NMF的な?) 単語１ 単語２ ⽂文書d 単語３ 単語の頻度度分布 単語1 単語2 単語3 単語１ 単語２ 単語３ ⽂文書d トピック分布 トピック1 トピック2 トピック3 各トピック =部分単体上の基底
- 47. 結局、LDAは何をやっているの？？ Collapsed Gibbs Samplingでこの計算をやるとは？ 各⽂文書d中の各単語wにトピックzを割り当ててみることを繰返すだけ θとφは積分消去でつぶし(collapseし)、条件付き分布 p(z|rest) を得る ⽂文書dのi番⽬目の単語wdiを除外してカウント値を作り、 その離離散分布 p(zdi|rest)から zdi をサンプリング zが分かればθもφも計算可能 その条件付き分布 p(z|rest) から実際にzをGibbs Sampling これは後述 ★ポイント１ ★ポイント２ ⽂文書dに割当られたトピックkのカウント 単語wに割当られたトピックkのカウント だけから分かる離離散分布 (めちゃeasy) (Coordinate Descent的に各単変量量ごとにやるだけ)
- 48. 論論⽂文で扱う他のトピックモデル (略略) LDA(Latent Dirichlet Allocation) PDP (Poisson Dirichlet Process) HDP (Hierarchical Dirichlet Process) ⾔言語モデルのrefine ⽂文書モデルのrefine
- 49. 本⽇日の発表の流流れ 1. 全体概要と前説 2. 準備1：離離散分布とDirichlet分布 3. 準備2：Walkerʼ’s alias method (1974) 離離散分布からの復復元抽出をO(1)でやる⽅方法 4. トピックモデル/⽣生成モデルのベイズ推定 何がしたいのか & どうやって求めるのか 5. Latent Dirichlet Allocation(LDA) 6. MCMC (Markov Chain Monte Carlo) Gibbs Sampling vs Metropolis-‐‑‒Hastings Sampling (non-‐‑‒MCMCなRejection Samplingとの関係を横⽬目で⾒見見つつ) 7. 本論論⽂文の紹介：分布の疎密分解+Alias method+MH step
- 50. 本⽇日の発表の流流れ 1. 全体概要と前説 2. 準備1：離離散分布とDirichlet分布 3. 準備2：Walkerʼ’s alias method (1974) 離離散分布からの復復元抽出をO(1)でやる⽅方法 4. トピックモデル/⽣生成モデルのベイズ推定 何がしたいのか & どうやって求めるのか 5. Latent Dirichlet Allocation(LDA) 6. MCMC (Markov Chain Monte Carlo) Gibbs Sampling vs Metropolis-‐‑‒Hastings Sampling (non-‐‑‒MCMCなRejection Samplingとの関係を横⽬目で⾒見見つつ) 7. 本論論⽂文の紹介：分布の疎密分解+Alias method+MH step
- 51. 寄り道：Rejection Sampling 1/2 ⽬目的：⽬目標分布pからxをサンプリング 分布pが訳の分からない分布な場合とか直接サンプリングは難しい… ⼿手段：サンプリングしやすい別の分布qからyをサンプリング 提案yをある条件を満たすときのみ受理理してxとして出⼒力力し、 満たさない場合yを棄却し、yのサンプリングをやり直し 提案yを作る分布qを提案分布(Proposal Distribution)と呼ぶ ある条件を⼯工夫すると、xが分布pのサンプルになるように出来る！ → Rejection Sampling (棄却サンプリング) ※無駄なサンプリングが少し増えるかもだけどqからのサンプリングでpからのサンプルを作れる！
- 52. 寄り道：Rejection Sampling 2/2 p(x)>0 ⇒ q(x)>0 かつ p(x)/q(x)≦c となる定数cが存在するような 分布qが提案分布ならば、以下の出⼒力力xは分布pからのサンプリング i) y ← qからのサンプル, u ← [0,1]の⼀一様乱数 ii) If u ≦ 1/c × p(y)/q(y)、x ← y (提案yを受理理) Else i)に戻る ※ q(x)は条件を満たせば何でも良良いが、p(x)とq(x)が違いすぎると 受理理される確率率率が下がり、無駄なサンプリングが増えるので効率率率悪 ＋ 定数cが存在しないか計算するのにコストがかかる場合も多い 参考) なぜこれでpからのサンプリングができるのか？→ cdfをcheck!
- 53. MCMC(1) Gibbs Sampling ⽬目的：⽬目標分布pからxをサンプリング xがp次元としてi番⽬目の要素xiとそれ以外x-‐‑‒iに対し 条件付き分布 P(xi |x-‐‑‒i) からのサンプリングを以下のように繰返す 各反復復 t において … ※ただし各条件付き分布からサンプリングが できる場合に限る iidじゃなく マルコフ連鎖に! 繰返すと分布が pに近づく 最初のほう(burn-‐‑‒ in)は捨てる Coordinate-‐‑‒Descent型 http://zoonek.free.fr/blosxom//R/2006-06-22_useR2006_rbiNormGiggs.png http://mikelove.files.wordpress.com/2008/09/gibbs.png
- 54. MCMC(2) Metropolis-‐‑‒Hastings Sampling ⽬目的：⽬目標分布pからxをサンプリング Gibbs Samplingの制約：各条件付き分布からサンプリングができる場合に限る → サンプリングしやすい別の分布q(y|x)を⽤用いて提案yを⽣生成し受理理/棄却 i) , ← [0,1]の⼀一様乱数 ii) If then Else (提案を受理理) (提案を棄却) 【驚くべき性質】提案分布q(y|x)はほぼ任意!! (独⽴立立q(y)とか、Gaussで乱歩とか) ただし、分布q(y|x)が真の分布p(y)から遠いと無駄が多くなり効率率率は下がる (Gibbsは100%受理理されるMetropolis-‐‑‒Hastingsの⼀一種と⾒見見る事もできる)
- 55. 本⽇日の発表の流流れ 1. 全体概要と前説 2. 準備1：離離散分布とDirichlet分布 3. 準備2：Walkerʼ’s alias method (1974) 離離散分布からの復復元抽出をO(1)でやる⽅方法 4. トピックモデル/⽣生成モデルのベイズ推定 何がしたいのか & どうやって求めるのか 5. Latent Dirichlet Allocation(LDA) 6. MCMC (Markov Chain Monte Carlo) Gibbs Sampling vs Metropolis-‐‑‒Hastings Sampling (non-‐‑‒MCMCなRejection Samplingとの関係を横⽬目で⾒見見つつ) 7. 本論論⽂文の紹介：分布の疎密分解+Alias method+MH step
- 56. 本⽇日の発表の流流れ 1. 全体概要と前説 2. 準備1：離離散分布とDirichlet分布 3. 準備2：Walkerʼ’s alias method (1974) 離離散分布からの復復元抽出をO(1)でやる⽅方法 4. トピックモデル/⽣生成モデルのベイズ推定 何がしたいのか & どうやって求めるのか 5. Latent Dirichlet Allocation(LDA) 6. MCMC (Markov Chain Monte Carlo) Gibbs Sampling vs Metropolis-‐‑‒Hastings Sampling (non-‐‑‒MCMCなRejection Samplingとの関係を横⽬目で⾒見見つつ) 7. 本論論⽂文の紹介：分布の疎密分解+Alias method+MH step
- 57. 本論論⽂文のkey idea: Metropolis-‐‑‒Hasting-‐‑‒Walker Sampling 以下の戦略略を「Metropolis-‐‑‒Hasting-‐‑‒Walker Sampling」と名付けた！ • 離離散分布pからのサンプリングをWalkerʼ’s Alias methodでO(1)にする。 • ここで分布pが(ちょっとだけ)変化して分布pʼ’になっているとき離離散分布pʼ’ からサンプリングしたい！ s t a l e な • O(1)でサンプリングできる変化前の(ちょっと前の)分布pを提案分布として Metropolis-‐‑‒Hasting Samplingを実⾏行行し、分布pʼ’からのサンプルを得る！ (pとpʼ’の変化がちょっとならほぼ即座に受理理されるのでとても効率率率的！) 本論論⽂文の趣旨は、トピックモデル推定においてGibbs Samplingの代わりにこの MHW Samplingを(疎密分解と共に)使うことにより、⾼高速化を図るというもの これを次に説明
- 58. 従来の知⾒見見 1/2 LDAのCollapsed Gibbs Sampling ⽂文書dのi番⽬目の単語wdiにトピックkが割当たる確率率率は以下で計算され (離離散分布)、以下の離離散分布からのサンプリングを繰返すだけでOK … … ⽂文書dに起こるトピックkの数単語wに割り当てられたトピックkの数 問題：⼀一回にO(k)かかるけどトピックの数は実データでは⼤大きい … … ⽂文書数が増えると⽂文書集合(コーパス)全体としては考えなければ いけないトピックの数も増えていく。 スパース性 ⼀一つの⽂文書が実際に含むトピックの数は⼀一定で⽂文書数に依らない (増えていく⽂文書集合全体が含むトピック数のうち少数) トピックの数
- 59. 従来の知⾒見見 2/2 LDAのCollapsed Gibbs Sampling ⽂文献[22]：上の右辺を以下のように分解して⼯工夫すると に! Sparse Sparse Dense ここがゼロになりやすい 単語wが含む トピック数 ⽂文書dが含む トピック数 は⽂文書数(⼩小)なら確かに で結局 に、、、 でも⽂文書数(⼤大)になると ⽂文献[22]の結果の問題
- 60. 本論論⽂文の内容 1/4 は⽂文書数(⼩小)なら確かに で結局 に、、、 でも⽂文書数(⼤大)になると 以下の分解により に改善！ ⽂文書dが含むトピック数 単語wに割当られたトピック数 Sparse Dense ⽂文献[22]の結果の問題 第１項、第２項のみに⽐比例例 する⼆二つの離離散分布を考える 離離散分布１ 離離散分布２ 正規化項(Σk右辺)を正規化項(Σk右辺)を
- 61. 本論論⽂文の内容 2/4 Sparse Dense 離離散分布１ 離離散分布２ 正規化項(Σk右辺)を正規化項(Σk右辺)を この２つの分布の混合分布を提案分布にしてMetropolis-‐‑‒Hasting Sampling
- 62. 本論論⽂文の内容 3/4 この２つの分布のmixtureを提案分布にしてMetropolis-‐‑‒Hasting Sampling sparseな項なので exactにサンプリング denseな項なので Alias methodでO(1)で取る (なので実際はちょっと前の分布) MHの原理理により以下で得るxは⽬目標分布からのサンプル i) 確率率率で から、確率率率 で から y をサンプリング ii) [0,1]の⼀一様乱数 u が「u ≦ min(1,π)」を満たす場合に y を x として受理理 正規化項が キャンセル!
- 63. 本論論⽂文の内容 4/4 Collapsed Gibbsの分布 p pを以下で分解し、denseな第2項はAlias Tableから求めた分布 q Metropolis-‐‑‒Hastings-‐‑‒Walker = qを提案分布としてpからMHサンプリング • 実際は単語⼀一個分だけの差でpとqが近いためすぐ受理理される。 (最初でもn=2, burn-‐‑‒inの後で極限分布に近づけばほぼn=1) • トピック数個のサンプルと正規化項の値をプールしてAlias Table⾃自体 はすぐ捨てる。(サンプルを使い果たしたら再度度Alias Tableを作る)
- 64. 実験結果(抜粋)
- 65. 実験結果(抜粋) ⼩小データではLDAよりPDPやHDPのほうが改善 → が、PubMedSmallやNYTimesの結果はないので PDPやHDPは⼤大きなデータではまだ難しい?? トピック数が増えるとAliasLDAによる 改善は⼤大きくなって⾏行行く (理理屈通り)
- 66. まとめ (再掲) サンプリング • 標本抽出 = ある分布に従う乱数⽣生成 トピック分布 1 2 3 4 5 6 7 8 乱数⽣生成 各語のトピックアロケーション 2, 4, 7, 7, 2, 8, 2, 4, … • LDAのGibbs Samplingでの推定はただ離離散分布からのサンプリングを 繰返せば良良いだけ(!)になる。(ただし分布が毎度度変わる) • 離離散分布からのサンプリングは(前処理理すれば) O(1)で⾏行行う⽅方法が！ → Walkerʼ’s alias method • ただ、実際のシチュエーションでは分布が毎回変わるので使えない。 …んですが、分布変わるとは⾔言え普通はそんなに⼤大きくは変わらない。 • そこでGibbsを⽌止めてMetropolis-‐‑‒Hasting(MH)にする。 ⼀一旦、MHの提案分布(の⼀一部)をAlias methodの古いサンプルで作り、 真の⽬目標分布とのズレはMHのAccept/Rejectステップで補正 • 提案分布 = ”疎な部分”+”密な部分”のmixture (後者を古い分布に)
- 67. 参考にした⽂文献 • 「Rによるモンテカルロ法⼊入⾨門」C.P.ロバート & G.カセーラ著, Springer, 2012. http://www.amazon.co.jp/dp/4621065270 • A Theoretical and Practical Implementation Tutorial on Topic Modeling and Gibbs Sampling, W. M. Darling, 2011. http://u.cs.biu.ac.il/~89-680/darling-lda.pdf • 統数研H24年年度度公開講座「確率率率的トピックモデル」, 持橋⼤大地・⽯石⿊黒勝彦, 2013. http://www.ism.ac.jp/~daichi/lectures/ISM-2012-TopicModels-daichi.pdf • Statistical Machine Learning, Topic Modeling, and Bayesian Nonparametrics 確率率率的 潜在変数モデル最前線 (DEIM2012 Tutorial), 佐藤⼀一誠, 2011. http://www.slideshare.net/issei_sato/deim2012-issei-sato! • Integrating Out Multinomial Parameters in Latent Dirichlet Allocation and Naive Bayes for Collapsed Gibbs Sampling, B. Carpenter, 2010. http://lingpipe.files.wordpress.com/2010/07/lda3.pdf • (まだ実物⾒見見てもいないけど何か良良さそう?) 「続・わかりやすいパターン認識識―教師なし学習⼊入⾨門―」 ⽯石井健⼀一郎郎・上⽥田修功, 2014. http://www.amazon.co.jp/dp/427421530X