Lecture 1 computational intelligence
- 1. Computational Intelligence Parveen Malik Assistant Professor School of Electronics Engineering KIIT University
- 2. Outline • Soft Computing Constituents • Fuzzy Set Theory • Set Theoretic Operations • Two Dimensional MFs
- 3. Soft Computing Constituents • Neural Network • Fuzzy Set Theory • Derivative Free Optimization( Genetic Algorithms) • Conventional AI Text Book : Chuen-Tsai Sun, Eiji Mizutani, and Jyh-Shing Roger Jang. “Neuro-Fuzzy and Soft Computing: A Computational Approach to Learning and Machine Intelligence”
- 4. Hidden Layer Output Layer Input Layer Neural Network
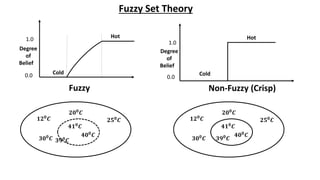
- 5. Fuzzy Set Theory Degree of Belief Fuzzy Hot Cold Degree of Belief Non-Fuzzy (Crisp) 1.0 0.0 Cold Hot 1.0 0.0 𝟒𝟏𝟎𝑪 𝟑𝟗𝟎𝑪 𝟒𝟎𝟎 𝑪 𝟐𝟎𝟎𝑪 𝟏𝟐𝟎𝑪 𝟑𝟎𝟎𝑪 𝟐𝟓𝟎 𝑪 𝟒𝟏𝟎𝑪 𝟑𝟗𝟎𝑪 𝟒𝟎𝟎 𝑪 𝟐𝟎𝟎𝑪 𝟏𝟐𝟎𝑪 𝟑𝟎𝟎𝑪 𝟐𝟓𝟎 𝑪
- 6. History of Conventional AI approaches
- 7. Fuzzy Set Theory Vs Classical Set Theory Classical Set Theory : • Crisp, clear or unambiguous boundary 𝐴 = 𝑥 𝑥 > 6} • Important tool for mathematic and computer science. • Sharp Transition between “Inclusion” and Exclusion”. • Incapable of addressing human concepts and thoughts which tend to be abstract and imprecise. A=“Tall Person” x =“Height” B= Water is hot” C=“Temp. is High”
- 8. Fuzzy Set Theory Vs Classical Set Theory Fuzzy Set Theory : • Introduced by “L.A.Zadeh” in 1965 paper “Fuzzy Sets” • Unclear or ambiguous boundary • Capable of addressing human concepts and thoughts which tend to be abstract and imprecise. A=“Tall Person” x =“Height” B= Water is hot” C=“Temp. is High” • Introduction of membership function • Gradual Transition from “Belong to a set” To “Not belong to set”.
- 9. Fuzzy Set Theory Definition 1.1 : Fuzzy Set and membership functions If X is a collection of objects denoted generically by x, then a fuzzy set A in X is defined as a set of ordered pairs: A= 𝒙, 𝝁𝑨(𝒙) | 𝒙 ∈ 𝑿 Where 𝜇𝐴(𝑥) is the membership function for the fuzzy set A Definition 1.2 : support The support of A fuzzy set A is the set of all points x in X such that 𝜇𝐴(𝑥) >0 support(A)= 𝒙 | 𝝁𝑨 𝒙 > 𝟎 Definition 1.3 : core The core of A fuzzy set A is the set of all points x in X such that 𝜇𝐴(𝑥) =1 core(A)= 𝒙|𝝁𝑨 𝒙 = 𝟎 Definition 1.4 : Normality A fuzzy set A is normal if its core is non-empty.
- 10. Fuzzy Set Theory Definition 1.5 : Cross Over Points A crossover point of a fuzzy set A is a point 𝑥 ∈ 𝑋 at which 𝜇𝐴(𝑥) = 0.5. crossover(A)= 𝒙|𝝁𝑨 𝒙 = 𝟎. 𝟓 Where 𝜇𝐴(𝑥) is the membership function for the fuzzy set A. Definition 1.6 : Fuzzy singleton A fuzzy set whose support is a single point in X with 𝜇𝐴(𝑥) = 1 is called a Fuzzy Singleton. Definition 1.7 : α-cut, strong α-cut α-cut, α-level set of a fuzzy set A is crisp set defined by 𝑨𝜶= 𝒙|𝝁𝑨 𝒙 ≥ 𝟎 Strong α-cut, strong α-level set of a fuzzy set A is defined by 𝑨𝜶 ′ = 𝒙|𝝁𝑨 𝒙 > 𝟎
- 11. Fuzzy Set Theory Definition 1.8 : Convexity A fuzzy set A is convex if and only if for any 𝑥1, 𝑥2 ∈ 𝑋 𝑎𝑛𝑑 for any λ ∈ 0,1 𝝁𝑨(𝝀𝒙𝟏 + (𝟏 − 𝝀)𝒙𝟐) ≥ Min 𝝁𝑨 𝒙𝟏 , 𝝁𝑨 𝒙𝟐 Alternatively, A is convex if all its 𝛼 − 𝑠𝑒𝑡𝑠 are convex. Definition 1.9 : Fuzzy numbers A fuzzy number A is a fuzzy set in the real line that satisfies the conditions for Normality and convexity. Definition 1.10 : Bandwidths of normal and convex fuzzy sets For a normal and convex fuzzy set, the bandwidth or width is defined as the distance between the two unique crossover points: 𝒘𝒊𝒅𝒕𝒉 𝑨 = 𝒙𝟐 − 𝒙𝟏 Where 𝝁𝑨 𝒙𝟏 = 𝝁𝑨(𝒙𝟐)=0.5
- 12. Fuzzy Set Theory Definition 1.11 : Symmetry A fuzzy set A is symmetric if its MF is symmetric around a certain point x=c , 𝝁𝑨 𝒄 + 𝒙 = 𝝁𝑨 𝒄 − 𝒙 for all 𝒙 ∈ 𝑿 Definition 1.12 : Open left, Open right, closed A fuzzy set A is open left if 𝒍𝒊𝒎𝒙→−∞𝝁𝑨 𝒙 =1 and 𝒍𝒊𝒎𝒙→+∞𝝁𝑨 𝒙 = 0 open right if 𝒍𝒊𝒎𝒙→−∞𝝁𝑨 𝒙 =0 and 𝒍𝒊𝒎𝒙→+∞𝝁𝑨 𝒙 = 1 Closed if 𝒍𝒊𝒎𝒙→−∞𝝁𝑨 𝒙 =𝒍𝒊𝒎𝒙→+∞𝝁𝑨 𝒙 =0
- 13. Set Theoretic Operations Definition 2.1 : Containment or Subset Fuzzy set A is contained in Fuzzy set B if and only if 𝑨 ⊆ 𝑩 ⇔ 𝝁𝑨 𝒙 ≤ 𝝁𝑩 𝒙 Definition 2.2 : Union (Disjunction) The union of two sets A and B is a set C (𝐴 ∪ B) whose MF is related by 𝝁 𝒙 = max {𝝁𝑨 𝒙 , 𝝁𝑩 𝒙 } = 𝝁𝑨 𝒙 ˅ 𝝁𝑩 𝒙 Definition 2.3 : Intersection (Conjunction) The intersection of two sets A and B is a set C (𝐴 ∩ B) whose MF is related by 𝝁 𝒙 = min {𝝁𝑨 𝒙 , 𝝁𝑩 𝒙 } = 𝝁𝑨 𝒙 ˄ 𝝁𝑩 𝒙
- 14. Set Theoretic Operations Definition 2.4 : Complement (Negation) The complement of Fuzzy set A is ഥ 𝐀 ¬𝐀 𝐨𝐫 𝐍𝐎𝐓 𝐀 𝝁ഥ 𝑨 𝒙 = 𝟏 − 𝝁𝑨 𝒙 Definition 2.5 : Cartesian product and co-product Let A and B be fuzzy sets in X and Y respectively. The Cartesian product of A and B denoted by 𝑨 × 𝑩 , 𝝁𝑨×𝑩 𝒙, 𝒚 = min {𝝁𝑨 𝒙 , 𝝁𝑩 𝒚 } The Co- product of A and B denoted by A + B, 𝝁𝑨+𝑩 𝒙, 𝒚 = max {𝝁𝑨 𝒙 , 𝝁𝑩 𝒚 }
- 15. Two Dimensional MFs Definition 3.1 : Cylindrical extensions of 1D fuzzy sets If A is a fuzzy set in X, then its cylindrical extension in 𝑿 × 𝒀 is a fuzzy set c(A) defined by 𝒄(𝑨) = න 𝑿×𝒀 𝝁𝑨(𝒙)/(𝒙, 𝒚)
- 16. Two Dimensional MFs Definition 3.1 : Projections of fuzzy sets If R be a two-dimensional fuzzy set on 𝑿 × 𝒀. The projections of R onto X and Y are defined as 𝑹𝑿 = න 𝑋 𝒎𝒂𝒙 {𝝁𝑹(𝒙, 𝒚)} /𝒙 𝑹𝒀 = න 𝑌 𝒎𝒂𝒙 {𝝁𝑹(𝒙, 𝒚)} /𝒚