Lecture_04.2.pptx

Stack & QueueApplications
Course Code: CSC 2106
Dept. of Computer Science
Faculty of Science and Technology
Lecturer No: 4.2 Week No: 5 Semester: Spring 20-21
Lecturer: Nazia Alfaz
nazia.alfaz@aiub.edu
Course Title: Data Structure (Theory)

Lecture Outline
1. Applications of Stack & Queue
2. Algebraic Expression
3. Infix, Postfix, Prefix
4. Infix
5. Operator Precedence and Associativity
6. Infix Expression is Hard to Parse
7. Examples of Infix to Postfix & Prefix
8. Parentheses Check Using Stack
9. Converting Postfix Expression Using Stack & Queue
10. Evaluating Postfix Expression Using Stack & Queue
11. Books
2. References

Applications of Stack & Queue
 Syntax parsing, Parenthesis check [Stack]
 Expression evaluation and Expression conversion. [Stack & Queue] [Can also be
achieved using only Stack]
 Banking Transaction View [Stack]
 You view the last transaction first.
 Backtracking and implementation of recursive function, calling function. [Stack]
 Towers of Hanoi [Stack]
 Keeping Track of Printing Jobs [Queue]

Algebraic Expression
 An algebraic expression is a legal combination of operands and the operators.
 Operand is the quantity (unit of data) on which a mathematical operation is
performed.
 Operand may be a variable like x,y,z or a constant like 5,4,0,9,1 etc.
 Operator is a symbol which signifies a mathematical or logical operation between
the operands. Example of familiar operators include +,-,*,/,^,%
 Considering these definitions of operands and operators now we can write an
example of expression as: x + y * z

Infix, Postfix and Prefix Expressions
 INFIX: The expressions in which operands surround the operator, i.e. operator is in
between the operands. e.g. x+y, 6*3 etc. The infix notation is the general way we
write an expression.
 POSTFIX: Also Known as Reverse Polish Notation (RPN). The operator comes after
the operands, i.e. operator comes post of the operands, so the name postfix. e.g.
xy+, xyz+* etc.
 PREFIX: Also Known as Polish notation. The operator comes before the operands, i.e.
operator comes pre of the operands, so the name prefix. e.g. +xy, *+xyz etc.

Infix
 To our surprise INFIX notations are not as simple as they seem specially while
evaluating them. To evaluate an infix expression we need to consider Operators’
Precedence and Associative property
 For example expression 3+5*4 evaluate to
32 = (3+5)*4
or
23 = 3+(5*4)
 Operator precedence and associativity governs the evaluation order of an
expression.
 An operator with higher precedence is applied before an operator with lower
precedence.
 Same precedence order operator is evaluated according to their associativity
order.

Infix
 To our surprise INFIX notations are not as simple as they seem specially while
evaluating them. To evaluate an infix expression we need to consider Operators’
Precedence and Associative property
 For example expression 3+5*4 evaluate to
32 = (3+5)*4 - Wrong
or
23 = 3+(5*4) - Correct
 Operator precedence and associativity governs the evaluation order of an
expression.
 An operator with higher precedence is applied before an operator with lower
precedence.
 Same precedence order operator is evaluated according to their associativity
order.

Operator Precedence and
Associativity

Infix Expression Is HardTo Parse
 Need operator priorities, tie breaker, and delimiters.
 This makes the evaluation of expression more difficult than is necessary for the
processor.
 Both prefix and postfix notations have an advantage over infix that while evaluating
an expression in prefix or postfix form we need not consider the Precedence and
Associative property.
 The expression is scanned from user in infix form; it is converted into prefix or postfix
form and then evaluated without considering the parenthesis and priority of the
operators.
 So, it is easier (complexity wise) for the processor to evaluate expressions that are in
these forms.

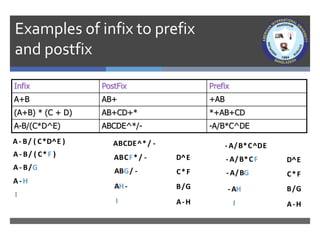
Infix PostFix Prefix
A+B AB+ +AB
(A+B) * (C + D) AB+CD+* *+AB+CD
A-B/(C*D^E) ABCDE^*/- -A/B*C^DE
ABCDE^* / -
A - B/ ( C*D^E )
A- B/ ( C*F )
A- B/G
A-H
I
ABCF* / - D E
^
C F
*
ABG/ -
B G
/
AH-
A H
-
I
- A/B*C^DE
D E
^
C F
*
B G
/
A H
-
I
- A/B*CF
- A/BG
- AH
Examples of infix to prefix
and postfix

Evaluation
Infix Postfix Prefix
(X+Y) * (M-N) XY+MN-* *+XY-MN
(2+4) * (8-6) 24+86-* *+24-86
6*2 62* *62
12 12 12
Let, X=2; Y=4; M=8; N=6
 Infix = <operand> <operator> <operand>
 Postfix = <operand> <operand> <operator>
 Prefix = <operator> <operand> <operand>

Parentheses Check Using Stack
Using Stack, we can check whether an expression has its parenthesis properly placed; i.e.,
whether its opening and closing parentheses match with each other. For example, let’s
take the expression (x{x[]}x)
We will read the expression as a string and for each character we will do the following
three things:
1. Whenever we get an opening parenthesis, we will push it into the stack.
2. When we get a closing parenthesis we will check that with the top of the stack. If the
top of the stack has the same type of opening parenthesis, we will pop it.
3. We skip the character in the string which is not a parenthesis.
Finally if you have reached the end of the expression and the stack is also empty, that
means the expression is “well formed”. In any other case, the expression is “not well
formed”.

Parentheses Check Using Stack
(x{x[]}x)
We will read the expression as a string and for each character we will do the following
three things:
1. Whenever we get an opening parenthesis, we will push it into the stack.
2. When we get a closing parenthesis we will check that with the top of the stack. If
the top of the stack has the same type of parenthesis but an opening one, we will
pop it.
3. We skip the character in the string which is not a parenthesis.
This expression is
“well formed”

2 * 6 / ( 4 - 1 ) +
Infix Expression: 2*6/(4-1)+5*3
Add ')' to the end of Infix; Push( '(' );
do{
OP = next symbol from left of Infix;
if OP is OPERAND then EnQueue( OP );
else if OP is OPERATOR then{
if OP = '(' then Push( OP );
else if OP = ')' then{
while TopElement() != '(' do{
Enqueue(TopElement());
Pop();
}
Pop();
}else{
while Precedence( OP ) <= Precedence( TopElement() ) do{
Enqueue(TopElement());
Pop();
}
Push( OP );
}
}while !IsEmpty();
Infix
Postfix
Stack
2 * 6 / ( 4 - 1 ) +
2 6 * 4 1 - / 5 3 * +
* ( -
*
/
+
OPERATOR
OPERAND
/ = StackTop( * )
*  StackTop( ( )
/  StackTop( ( )
(
)
+ < StackTop( / )
+  StackTop( ( )
*  StackTop( + )
End of Expression
(
-  StackTop( ( )
Converting Infix to Postfix
Using Stack & Queue

2 6 * 4 1 - / 5 3 * + )
Evaluating Postfix Expression
Using Stack & Queue
Postfix Expression: 26*41-/53*+
EnQueue( ')' );
while ( FrontElement() != ')' ) do{
OP = FrontElement();
DeQueue();
if OP is OPERAND then Push( OP );
else if OP is OPERATOR then{
OperandRight = TopElement();
Pop();
OperandLeft = TopElement();
Pop();
x = Evaluate(OperandLeft, OP, OperandRight);
Push(x);
}
}
Result = TopElement();
Pop();
cout << Result;
Postfix
Stack
2 6 * 4 1 - / 5 3 * +
2 4 1
3
6
12
OPERATOR
OPERAND
Evaluate( 2, '*', 6 ) = 12
Evaluate( 4, '+', 15 ) = 19
‘)‘
Evaluate( 5, '*', 3 ) = 15
Evaluate( 12, '/', 3 ) = 4
Evaluate( 4, '-', 1 ) = 3
End of Expression
)
4 5 3
15
19
Expression Result = 19

Books
 “Schaum's Outline of Data Structures with C++”. By John R. Hubbard
 “Data Structures and Program Design”, Robert L. Kruse, 3rd Edition, 1996.
 “Data structures, algorithms and performance”, D. Wood, Addison-Wesley, 1993
 “Advanced Data Structures”, Peter Brass, Cambridge University Press, 2008
 “Data Structures and Algorithm Analysis”, Edition 3.2 (C++ Version), Clifford A.
Shaffer, Virginia Tech, Blacksburg, VA 24061 January 2, 2012
 “C++ Data Structures”, Nell Dale and David Teague, Jones and Bartlett Publishers,
2001.
 “Data Structures and Algorithms with Object-Oriented Design Patterns in C++”,
Bruno R. Preiss,

References
1. http://www.cs.uregina.ca/Links/class-info/210/Stack/
2. http://www.cs.csi.cuny.edu/~zelikovi/csc326/data/assignment5.htm

Lecture_04.2.pptx

More Related Content

Similar to Lecture_04.2.pptx (20)

Recently uploaded (20)

Lecture_04.2.pptx