Lesson05_Static11

Statistics for Management Fundamentals of Hypothesis Testing

Lesson Topics 1. What is a Hypothesis? Hypothesis Testing Methodology Hypothesis Testing Process Level of Significance, a Errors in Making Decisions 2. Hypothesis Testing: Steps Z Test for the Mean (s Known) Connection to Confidence Interval Estimation Hypothesis Testing Methodology

A hypothesis is an assumption about the population parameter. A parameter is a Population mean or proportion The parameter must be identified before analysis. I assume the mean GPA of this class is 3.5! © 1984-1994 T/Maker Co. 1. What is a Hypothesis?

States the Assumption (numerical) to be tested e.g. The average # TV sets in US homes is at least 3 ( H 0 :  3 ) Begin with the assumption that the null hypothesis is TRUE. (Similar to the notion of innocent until proven guilty ) The Null Hypothesis, H 0 Always contains the ‘ = ‘ sign The Null Hypothesis may or may not be rejected.

Is the opposite of the null hypothesis e.g. The average # TV sets in US homes is less than 3 ( H 1 :  < 3 ) Never contains the ‘=‘ sign The Alternative Hypothesis may or may not be accepted The Alternative Hypothesis, H 1

Steps: State the Null Hypothesis ( H 0 :   3) State its opposite, the Alternative Hypothesis ( H 1 :  < 3) Hypotheses are mutually exclusive & exhaustive Sometimes it is easier to form the alternative hypothesis first. Identify the Problem

Population Assume the population mean age is 50. (Null Hypothesis) REJECT The Sample Mean Is 20 Sample Null Hypothesis Hypothesis Testing Process No, not likely!

Sample Mean  = 50 Sampling Distribution It is unlikely that we would get a sample mean of this value ... ... if in fact this were the population mean. ... Therefore, we reject the null hypothesis that  = 50. 20 H 0 Reason for Rejecting H 0

Defines Unlikely Values of Sample Statistic if Null Hypothesis Is True Called Rejection Region of Sampling Distribution Designated   (alpha) Typical values are 0.01, 0.05, 0.10 Selected by the Researcher at the Start Provides the Critical Value(s) of the Test Level of Significance, 

Level of Significance,  and the Rejection Region H 0 :   3 H 1 :  < 3 0 0 0 H 0 :   3 H 1 :  > 3 H 0 :   3 H 1 :   3    /2 Critical Value(s) Rejection Regions

Type I Error Reject True Null Hypothesis Has Serious Consequences Probability of Type I Error Is  Called Level of Significance Type II Error Do Not Reject False Null Hypothesis Probability of Type II Error Is  (Beta) Errors in Making Decisions

H 0 : Innocent Jury Trial Hypothesis Test Actual Situation Actual Situation Verdict Innocent Guilty Decision H 0 True H 0 False Innocent Correct Error Do Not Reject H 0 1 -  Type II Error (  ) Guilty Error Correct Reject H 0 Type I Error (  ) Power (1 -  ) Result Possibilities

  Reduce probability of one error and the other one goes up.  &   Have an Inverse Relationship

True Value of Population Parameter Increases When Difference Between Hypothesized Parameter & True Value Decreases Significance Level  Increases When  Decreases Population Standard Deviation  Increases When   Increases Sample Size n Increases When n Decreases Factors Affecting Type II Error,       n

Convert Sample Statistic (e.g., ) to Standardized Z Variable Compare to Critical Z Value(s) If Z test Statistic falls in Critical Region, Reject H 0 ; Otherwise Do Not Reject H 0 Z-Test Statistics (  Known) Test Statistic X

1. State H 0 H 0 :  3 2. State H 1 H 1 :  3. Choose   = .05 4. Choose n n = 100 5. Choose Test : Z Test (or p Value) 2. Hypothesis Testing: Steps Test the Assumption that the true mean # of TV sets in US homes is at least 3.

6. Set Up Critical Value(s) Z = -1.645 7. Collect Data 100 households surveyed 8. Compute Test Statistic Computed Test Stat.= -2 9. Make Statistical Decision Reject Null Hypothesis 10. Express Decision The true mean # of TV set is less than 3 in the US households. Hypothesis Testing: Steps Test the Assumption that the average # of TV sets in US homes is at least 3. (continued)

Assumptions Population Is Normally Distributed If Not Normal , use large samples Null Hypothesis Has  or   Sign Only Z Test Statistic: 3. One-Tail Z Test for Mean (  Known)

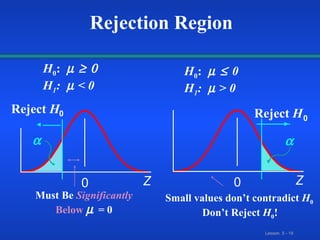
Z 0  Reject H 0 Z 0 Reject H 0  H 0 :  H 1 :  < 0 H 0 :  0 H 1 :  > 0 Must Be Significantly Below  = 0 Small values don’t contradict H 0 Don’t Reject H 0 ! Rejection Region

Does an average box of cereal contain more than 368 grams of cereal? A random sample of 25 boxes showed X = 372.5 . The company has specified   to be 15 grams. Test at the  0.05 level. 368 gm. Example: One Tail Test H 0 :  368 H 1 :  > 368 _

Z .04 .06 1.6 . 5495 . 5505 .5515 1.7 .5591 .5599 .5608 1.8 .5671 .5678 .5686 .5738 .5750 Z 0  Z = 1 1.645 .50 -. 05 .45 . 05 1.9 .5744 Standardized Normal Probability Table (Portion) What Is Z Given   = 0.05 ?  = .05 Finding Critical Values: One Tail Critical Value = 1.645

 = 0.05 n = 25 Critical Value: 1.645 Test Statistic: Decision: Conclusion: Do Not Reject at  = .05 No Evidence True Mean Is More than 368 Z 0 1.645 .05 Reject Example Solution: One Tail H 0 :  368 H 1 :  > 368

Does an average box of cereal contains 368 grams of cereal? A random sample of 25 boxes showed X = 372.5 . The company has specified   to be 15 grams. Test at the  0.05 level. 368 gm. Example: Two Tail Test H 0 :  368 H 1 :  368

 = 0.05 n = 25 Critical Value: ±1.96 Test Statistic: Decision: Conclusion: Do Not Reject at  = .05 No Evidence that True Mean Is Not 368 Z 0 1.96 .025 Reject Example Solution: Two Tail -1.96 .025 H 0 :  386 H 1 :  386

Connection to Confidence Intervals For X = 372.5oz,  = 15 and n = 25, The 95% Confidence Interval is: 372.5 - ( 1.96 ) 15 / 25 to 372.5 + ( 1.96 ) 15 / 25 or 366.62    378.38 If this interval contains the Hypothesized mean ( 368 ), we do not reject the null hypothesis. It does. Do not reject. _

Assumptions Population is normally distributed If not normal, only slightly skewed & a large sample taken Parametric test procedure t test statistic t-Test:  Unknown

Example: One Tail t-Test Does an average box of cereal contain more than 368 grams of cereal? A random sample of 36 boxes showed X = 372.5 , and  S= 15 . Test at the  0.01 level. 368 gm. H 0 :   368 H 1 :  368  is not given,

 = 0.01 n = 36, df = 35 Critical Value: 2.4377 Test Statistic: Decision: Conclusion: Do Not Reject at  = .01 No Evidence that True Mean Is More than 368 Z 0 2.4377 .01 Reject Example Solution: One Tail H 0 :  368 H 1 :  368

Involves categorical variables Fraction or % of population in a category If two categorical outcomes , binomial distribution Either possesses or doesn’t possess the characteristic Sample proportion ( p s ) 4. Proportions

Example:Z Test for Proportion Problem: A marketing company claims that it receives 4% responses from its Mailing. Approach: To test this claim, a random sample of 500 were surveyed with 25 responses. Solution: Test at the  = .05 significance level.

 = .05 n = 500 Do not reject at  = .05 Z Test for Proportion: Solution H 0 : p  .04 H 1 : p  .04 Critical Values:  1.96 Test Statistic: Decision: Conclusion: We do not have sufficient evidence to reject the company’s claim of 4% response rate. Z  p - p p (1 - p) n s = .04 -.05 .04 (1 - .04) 500 = -1.14 Z 0 Reject Reject .025 .025

5. Comparing two independent samples Comparing Two Means: Z Test for the Difference in Two Means (Variances Known) t Test for Difference in Two Means (Variances Unknown) Comparing two proportions Z Test for Differences in Two Proportions

Different Data Sources: Unrelated Independent Sample selected from one population has no effect or bearing on the sample selected from the other population. Use Difference Between the 2 Sample Means Use Pooled Variance t Test Independent Samples

Assumptions: Samples are Randomly and Independently drawn Data Collected are Numerical Population Variances Are Known Samples drawn are Large Test Statistic: Z Test for Differences in Two Means (Variances Known)

Assumptions: Both Populations Are Normally Distributed Or, If Not Normal, Can Be Approximated by Normal Distribution Samples are Randomly and Independently drawn Population Variances Are Unknown But Assumed Equal t Test for Differences in Two Means (Variances Unknown)

Developing the Pooled-Variance t Test (Part 1) Setting Up the Hypothesis: H 0 :  1   2 H 1 :  1 >  2 H 0 :  1 -  2 = 0 H 1 :  1 -  2  0 H 0 :  1 =  2 H 1 :  1   2 H 0 :  1   2  H 0 :  1 -  2  0 H 1 :  1 -  2 > 0 H 0 :  1 -  2  H 1 :  1 -  2 < 0 OR OR OR Left Tail Right Tail Two Tail  H 1 :  1 <  2

Developing the Pooled-Variance t Test (Part 2) Calculate the Pooled Sample Variances as an Estimate of the Common Populations Variance: = Pooled-Variance = Variance of Sample 1 = Variance of sample 2 = Size of Sample 1 = Size of Sample 2

t X X S n S n S n n df n n P                 1 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2   Hypothesized Difference Developing the Pooled-Variance t Test (Part 3) Compute the Test Statistic: ( ) ) ( ( ) ( ) ( ) ( ) n 1 n 2 _ _

You’re a financial analyst for Charles Schwab. Is there a difference in dividend yield between stocks listed on the NYSE & NASDAQ? You collect the following data: NYSE NASDAQ Number 21 25 Mean 3.27 2.53 Std Dev 1.30 1.16 Assuming equal variances, is there a difference in average yield (  = 0.05 )? © 1984-1994 T/Maker Co. Pooled-Variance t Test: Example

t X X S n n S n S n S n n P P                            1 2 1 2 2 1 2 2 1 1 2 2 2 2 1 2 2 2 3 27 2 53 0 1 510 21 25 2 03 1 1 1 1 21 1 1 30 25 1 1 16 21 1 25 1 1 510   . . . . . . . Calculating the Test Statistic: ( ( ( ( ( ( ( ( ( ( ( ) ) ) ) ) ) ) ) ) ) )

H 0 :  1 -  2 = 0 (  1 =  2 ) H 1 :  1 -  2  0 (  1   2 )  = 0.05 df = 21 + 25 - 2 = 44 Critical Value(s): Test Statistic: Decision: Conclusion: Reject at  = 0.05 There is evidence of a difference in means. t 0 2.0154 -2.0154 .025 Reject H 0 Reject H 0 .025 t    3 27 2 53 1 510 21 25 2 03 . . . . Solution

Z Test for Differences in Two Proportions Assumption: Sample is large enough

Lesson05_Static11

Recommended

More Related Content

What's hot (18)

Similar to Lesson05_Static11 (20)

More from thangv (17)

Recently uploaded (20)

Lesson05_Static11