Logic gates and its realization

May 10, 2020Download as PPTX, PDF2 likes2,232 views

Various logic gates are described with their logic symbol, truth table and the same are realized using Every Circuit app.

LOGIC GATES
 Logic gates are the basic building blocks of any digital
system.
 It is an electronic circuit having one or more than one
input and only one output.
 The relationship between the input and the output is
based on a certain logic.
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 1

CLASSIFICATION
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 2

SYMBOLS
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 3

BASIC LOGIC GATES
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 4

AND GATE
 The output of AND gate is high (‘1’) if all of its inputs are
high (‘1’).
 The output of AND gate is low (‘0’) if any one of its inputs
is low (‘0’).
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 5

LOGIC SYMBOL
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 6

TIMING DIAGRAM
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 7

TRUTH TABLE
A B Y = A.B
0 0 0
0 1 0
1 0 0
1 1 1
A B C Y = A.B.C
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 1
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 8

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 9

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 10

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 11

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 12

OR GATE
 The output of OR gate is high (‘1’) if any one of its inputs is
high (‘1’).
 The output of OR gate is low (‘0’) if all of its inputs are low
(‘0’).
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 13

LOGIC SYMBOL
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 14

TIMING DIAGRAM
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 15

TRUTH TABLE
A B Y = A+B
0 0 0
0 1 1
1 0 1
1 1 1
A B C Y =
A+B+C
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 16

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 17

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 18

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 19

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 20

NOT GATE
 The output of NOT gate is high (‘1’) if its input is low (‘0’).
 The output of NOT gate is low (‘0’) if its input is high (‘1’).
 It is clear that NOT gate simply inverts the given input.
 Since NOT gate simply inverts the given input, therefore it
is also known as Inverter Gate.
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 21

LOGIC SYMBOL
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 22

TIMING DIAGRAM
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 23

TRUTH TABLE
A Y = A’
0
1
1
0
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 24

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 25

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 26

UNIVERSAL LOGIC GATES
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 27

NAND GATE
 A NAND Gate is constructed by connecting a NOT Gate at
the output terminal of the AND Gate.
 The output of NAND gate is high (‘1’) if at least one of its
inputs is low (‘0’).
 The output of NAND gate is low (‘0’) if all of its inputs are
high (‘1’).
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 28

LOGIC SYMBOL
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 29

TIMING DIAGRAM
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 30

TRUTH TABLE
A B Y =
(A.B)’
0 0 1
0 1 1
1 0 1
1 1 0
A B C Y =
(A.B.C)’
0 0 0 1
0 0 1 1
0 1 0 1
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 0
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 31

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 32

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 33

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 34

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 35

NOR GATE
 A NOR Gate is constructed by connecting a NOT Gate at
the output terminal of the OR Gate.
 The output of OR gate is high (‘1’) if all of its inputs are low
(‘0’).
 The output of OR gate is low (‘0’) if any of its inputs is high
(‘1’).
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 36

LOGIC SYMBOL
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 37

TIMING DIAGRAM
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 38

TRUTH TABLE
A B Y =
(A+B)’
0 0 1
0 1 0
1 0 0
1 1 0
A B C Y =
(A+B+C)’
0 0 0 1
0 0 1 0
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 0
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 39

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 40

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 41

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 42

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 43

OTHER LOGIC GATES
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 44

EXOR GATE
 The logic gate which gives high output (i.e., 1) if either
input A or input B but not both are high (i.e. 1) is called
exclusive OR gate or the XOR gate.
 It may be noted that if both the inputs of the XOR gate are
high, then the output is low (i.e., 0).
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 45

LOGIC SYMBOL
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 46

TRUTH TABLE
A B Y =
A ⊕ B
0 0 0
0 1 1
1 0 1
1 1 0
A B C Y =
A ⊕ B ⊕ C
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 0
1 0 0 1
1 0 1 0
1 1 0 0
1 1 1 1
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 47

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 48

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 49

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 50

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 51

EXNOR GATE
 The logic function implemented by a 2-input Ex-NOR gate
is given as “when both A AND B are the SAME” will give an
output at Q.
 In general, an Exclusive-NOR gate will give an output value
of logic “1” ONLY when there are an EVEN number of 1’s on
the inputs to the gate (the inverse of the Ex-OR gate)
except when all its inputs are “LOW”.
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 52

LOGIC SYMBOL
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 53

TRUTH TABLE
A B Y =
(A ⊕ B)’
0 0 1
0 1 0
1 0 0
1 1 1
A B C Y =
(A ⊕ B ⊕ C)’
0 0 0 1
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 0
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 54

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 55

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 56

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 57

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 58

LOGIC GATES and THEIR ICs
IC NUMBER NAME OF THE GATE
7400 NAND
7402 NOR
7404 NOT
7408 AND
7432 OR
7486 EXOR/ XOR/ EOR
74266 EXNOR/ XNOR/ ENOR
09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 59

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 60

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 61

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 62

09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 63

This document discusses digital logic gates and circuits. It describes the basic logic gates - NOT, AND, OR, NAND, NOR, XOR, XNOR - and how each is represented by a truth table. Combinational circuits are defined as having outputs determined solely by current inputs, while sequential circuits can store past input states in memory elements like flip-flops and registers. Examples of common combinational circuits are provided.

Array pptKaushal Mehta

This document discusses arrays in three sentences or less: Arrays allow storing and accessing multiple values under a single name, with each value stored in consecutive memory locations. Arrays come in one-dimensional, two-dimensional, and multi-dimensional forms and can be accessed using indexes. Common array operations include initialization, accessing elements, searching, sorting, and performing operations on all elements using loops.

Ordinary differential equationsAhmed Haider

The document is an introduction to ordinary differential equations prepared by Ahmed Haider Ahmed. It defines key terms like differential equation, ordinary differential equation, partial differential equation, order, degree, and particular and general solutions. It then provides methods for solving various types of first order differential equations, including separable, homogeneous, exact, linear, and Bernoulli equations. Specific examples are given to illustrate each method.

School management software proposalMohammad Sayem

The document discusses a school management software proposal. It describes how the software can help store, control, and centralize all school activities and operations. It maintains student and teacher data and helps the administration department function effectively through integrated, user-friendly tools. The software handles key functions like admissions, scheduling, fees collection, HR, exams, inventory, and attendance. It provides a way to automate and control these processes to help schools run efficiently.

Microcontroller based transformer protectioAminu Bugaje

This document provides an introduction and background to a project on designing a microcontroller-based transformer protection system. It discusses how transformers are critical components in power systems that require protection against faults like short circuits, overcurrent and overvoltage. The document then reviews previous work on transformer protection and outlines the objectives of this project, which are to design current and voltage sensing circuits, develop a microcontroller algorithm for overload, overvoltage and undervoltage protection, and test the system's performance. The chapter concludes by outlining the scope and limitations of the project, which involves both hardware and software design to develop a protection system that can monitor transformer parameters and trip circuit breakers or relays during faults.

KCL and KVL140120109032

This document discusses Kirchhoff's laws for circuits and networks. It provides examples of applying Kirchhoff's Current Law (KCL) and Kirchhoff's Voltage Law (KVL) to solve for unknown currents and voltages in circuits. KCL states that the algebraic sum of currents at any node is zero. KVL states that the algebraic sum of the voltages around any closed loop is zero. The document also defines related terms like nodes, branches, and loops and shows voltage rises and drops.

Programming in c Arraysjanani thirupathi

An array is a collection of data that holds a fixed number of values of the same type. Arrays allow storing multiple values in a single variable through indices. There are one-dimensional, two-dimensional, and multi-dimensional arrays. One-dimensional arrays use a single subscript, two-dimensional arrays use two subscripts like rows and columns, and multi-dimensional arrays can have more than two subscripts. Arrays can be initialized during declaration with values or initialized at runtime by user input or other methods. Elements are accessed using their indices and operations can be performed on the elements.

Transistor as a switch jignesh prajapati

Transistors can be used as switches by operating them in either saturation or cut-off regions. In saturation, the transistor is fully on with maximum collector current and minimum voltage drop. In cut-off, it is fully off with zero collector current and maximum voltage. Transistor switches allow interfacing low voltage digital logic to devices requiring higher voltages and currents, and can be used to control lamps, relays, motors and other loads. The base resistor value must be calculated to fully turn the transistor on above a given input voltage.

Combinational circuitSIVALAKSHMIPANNEERSE

BOOLEAN ALGEBRA & LOGIC GATEIdeal Eyes Business College

latchesUnsa Shakir

Latches are asynchronous electronic logic circuits with two stable output states. There are four main types of latches: D, T, SR, and JK latches. An SR latch has two inputs - SET (S) and RESET (R) - and two complementary outputs (Q and Q'). The state of the latch depends on whether input S or R is activated. A D latch similarly has one data input and two complementary outputs, but removes invalid states that can occur in an SR latch. Latches can be either active-high or active-low, depending on whether a high or low input triggers a state change.

Practical Uses of Logic GatesAbiral Gautam

Latches and flip flopShuaib Hotak

This document discusses latches and flip flops, which are types of sequential logic circuits. It describes the basic components and functioning of latches like SR latches, D latches, and gated latches. For flip flops, it covers SR flip flops, D flip flops, JK flip flops, and master-slave flip flops. The key differences between latches and flip flops are that latches do not have a clock input while flip flops are edge-triggered by a clock signal. Latches and flip flops are used as basic storage elements in more complex sequential circuits and in computer components like registers and RAM.

Presentation On Logic Gate Nazrul Islam

This presentation introduces logic gates. It defines a logic gate as a building block of digital circuits that takes two or more inputs and outputs one value based on Boolean algebra. Common logic gates are then described, including AND, OR, and NOT gates. NAND and NOR gates are universal gates that can be used to represent all other logic functions. Exclusive gates like XOR and XNOR are also discussed. Finally, compound gates are defined as combinations of basic logic gates to form more complex functions.

OR, AND, NOT GatesMd. Nazmus Saqib Khan

This document presents a presentation on logic gates such as OR, AND, and NOT gates. It begins with an introduction to logic gates and Boolean algebra. It then describes the basic OR, AND, and NOT gates. The presentation continues by explaining some other gates like NAND, NOR, XOR and XNOR gates. It provides an example of combining gates. Finally, it proposes a real-world problem of designing a car circuit to sound a buzzer based on speed or seatbelt use and shows the logic gate implementation of the solution.

Combinational circuitsSARITHA REDDY

This document discusses combinational logic circuits such as adders, subtractors, multipliers, decoders, and multiplexers. It provides circuit diagrams and truth tables for half adders, full adders, half subtractors, full subtractors, decoders, and multiplexers. It also describes how to build binary adders and subtractors using these basic components and how multiplication of binary numbers is performed.

MultiplexersDrSonali Vyas

A multiplexer is a device that selects one of several analog or digital input signals and forwards the selected input into a single line. It has multiple data inputs, a single output, and select lines that determine which input is directed to the output. A demultiplexer performs the opposite function, taking a single input and distributing it to one of multiple outputs based on the select lines. Multiplexers and demultiplexers come in various configurations depending on the number of inputs and outputs, such as 2:1, 4:1, 16:1 or 32:1. They are basic building blocks used in digital systems and communication networks to efficiently route signals.

Logic gates - AND, OR, NOT, NOR, NAND, XOR, XNOR Gates.Satya P. Joshi

BOOLEAN ALGEBRA AND LOGIC GATE Tamim Tanvir

Boolean algebra and logic circuits were introduced. Boolean algebra uses binary numbers (0,1) and logical operations like AND, OR, and NOT to simplify logic expressions. Basic logic gates like AND, OR, and NOT were explained. Logic circuits can be built using combinations of logic gates to perform complex logical functions. Boolean algebra is used to simplify logic circuits and increase the efficiency of digital devices like computers.

Digital electronicsAfghanistan civil aviation institute

This document provides an overview of digital electronics and related topics including: - Digital electronics deals with data and codes represented by two conditions - 0 and 1. Circuits are made from logic gates. - Early computers used mechanical switches and relays before transistors were developed. Integrated circuits allowed circuits to be placed on silicon chips. - Analog signals are continuous while digital signals represent data discretely as 0s and 1s. Conversion between analog and digital is often needed. - Common numbering systems like binary, decimal, octal and hexadecimal are explained along with operations on them. Boolean algebra which digital circuits are based on is also introduced.

Shift RegistersAbhilash Nair

Shift registers are digital circuits composed of flip-flops that can shift data from one stage to the next. They can be configured for serial-in serial-out, serial-in parallel-out, parallel-in serial-out, or parallel-in parallel-out data movement. Common applications include converting between serial and parallel data, temporary data storage, and implementing counters. MSI shift registers like the 74LS164 and 74LS166 provide 8-bit shift register functionality.

Digital logic gates and Boolean algebraSARITHA REDDY

The document discusses digital logic gates and Boolean algebra. It defines logic gates as electronic circuits that make logic decisions. Common logic gates include OR, AND, and NOT gates. Boolean algebra uses truth values of 0 and 1 instead of numbers, and has fundamental laws and operations for AND, OR, and NOT. Boolean algebra can be used to simplify logical expressions and save gates in digital circuit design.

Digital Logic circuitkavitha muneeshwaran

This document provides an overview of digital logic circuits and sequential circuits. It discusses various logic gates like OR, AND, NOT, NAND, NOR and XOR gates. It explains their truth tables and symbols. It also covers Boolean algebra, map simplification using K-maps, combinational circuits like multiplexers, demultiplexers, encoders and decoders. Finally, it describes different types of flip-flops like SR, D, JK and T flip-flops which are used to build sequential circuits that have memory and can store past states.

EncoderMahmudul Hasan

This presentation introduces encoders. It discusses that an encoder is a combinational circuit that performs the reverse operation of a decoder, with a maximum of 2n inputs and n outputs. The simplest encoder is a 2n-to-n binary encoder, where one of the 2n inputs is 1 and the output is an n-bit binary number representing the activated input. An example of an 8-to-3 binary encoder is shown, where only one of the 8 inputs can be activated at a time, and the 3 outputs represent the activated input in binary code.

Digital Logic & Design (DLD) presentationfoyez ahammad

Half subtracterawais ahmad

The half subtractor is a digital circuit that takes two binary inputs, A and B, and produces the difference and borrow outputs. It uses an XOR gate to produce the difference output of A'B + AB' and an AND gate with an inverter to produce the borrow output of AB'. The document provides the truth table and circuit diagram for a half subtractor and describes building a half subtractor circuit on a breadboard to verify its functionality based on the truth table.

Programmable logic devicesISMT College

This document discusses programmable logic devices (PLDs), including their basic components and types. PLDs are integrated circuits that can be configured by the user to perform different logic functions. They contain programmable AND and OR gates that allow the user to define the logic function by programming the connections between the gates. Common types of PLDs include PROM, PAL, and PLA, which differ in whether their AND gates and/or OR gates are programmable. The document provides examples and diagrams to illustrate how basic logic functions can be implemented using each type of PLD.

sequential circuitsUnsa Shakir

Sequential circuits have outputs determined by both the current inputs and previous outputs due to the inclusion of memory elements. Combinational circuits only have outputs determined by the current inputs. Sequential circuits contain logic gates arranged in parallel and feedback loops allowing the circuit to store past states, while combinational circuits only depend on the current input combination. There are different types of sequential circuits including those controlled by a clock signal from a clock generator that produces periodic pulses defining the circuit timing.

logic circuits_walla2_c++_download_Welcome.pdfyyu8u

Logic gateNazim Naeem

The document discusses digital logic gates and their usage in computers. It describes that logic gates combine electrical pulses following logical rules and are the basic components used to move data and instructions through a computer. The three basic logic gates are AND, OR, and NOT. These gates can be combined to perform more complex logic functions and operations like addition. Adders are constructed using networks of half adders and full adders to add binary numbers.

More Related Content

What's hot (20)

Combinational circuitSIVALAKSHMIPANNEERSE

BOOLEAN ALGEBRA & LOGIC GATEIdeal Eyes Business College

latchesUnsa Shakir

Practical Uses of Logic GatesAbiral Gautam

Latches and flip flopShuaib Hotak

Presentation On Logic Gate Nazrul Islam

OR, AND, NOT GatesMd. Nazmus Saqib Khan

Combinational circuitsSARITHA REDDY

MultiplexersDrSonali Vyas

Logic gates - AND, OR, NOT, NOR, NAND, XOR, XNOR Gates.Satya P. Joshi

BOOLEAN ALGEBRA AND LOGIC GATE Tamim Tanvir

Digital electronicsAfghanistan civil aviation institute

Shift RegistersAbhilash Nair

Digital logic gates and Boolean algebraSARITHA REDDY

Digital Logic circuitkavitha muneeshwaran

EncoderMahmudul Hasan

Digital Logic & Design (DLD) presentationfoyez ahammad

Half subtracterawais ahmad

Programmable logic devicesISMT College

sequential circuitsUnsa Shakir

Combinational circuitSIVALAKSHMIPANNEERSE

BOOLEAN ALGEBRA & LOGIC GATEIdeal Eyes Business College

latchesUnsa Shakir

Practical Uses of Logic GatesAbiral Gautam

Latches and flip flopShuaib Hotak

Presentation On Logic Gate Nazrul Islam

OR, AND, NOT GatesMd. Nazmus Saqib Khan

Combinational circuitsSARITHA REDDY

MultiplexersDrSonali Vyas

Logic gates - AND, OR, NOT, NOR, NAND, XOR, XNOR Gates.Satya P. Joshi

BOOLEAN ALGEBRA AND LOGIC GATE Tamim Tanvir

Digital electronicsAfghanistan civil aviation institute

Shift RegistersAbhilash Nair

Digital logic gates and Boolean algebraSARITHA REDDY

Digital Logic circuitkavitha muneeshwaran

EncoderMahmudul Hasan

Digital Logic & Design (DLD) presentationfoyez ahammad

Half subtracterawais ahmad

Programmable logic devicesISMT College

sequential circuitsUnsa Shakir

Similar to Logic gates and its realization (20)

logic circuits_walla2_c++_download_Welcome.pdfyyu8u

Logic gateNazim Naeem

logic gates.pptxaravind649229

Logic gates are fundamental building blocks of digital systems that make decisions by producing different output levels based on combinations of input levels. The two levels are high/true/1 and low/false/0. Truth tables list all possible input combinations and corresponding outputs. Common logic gates include AND, OR, NOT, NAND, and NOR. NAND and NOR gates are considered universal gates as they can perform all basic logic functions.

CseAarti Masal

The document describes experiments to be performed on digital logic circuits. It includes experiments to verify truth tables of basic logic gates like AND, OR, NOT; implement Boolean functions using gates; and minimize Boolean functions using Karnaugh maps. The experiments are to be done using integrated circuits of logic gates on an IC trainer kit. Students will observe the output LEDs for different input combinations to verify truth tables and logic functions.

digital electronics .pptxAjaykumar967485

This document discusses various types of logic gates. It begins with an introduction to logic gates and their basic components. It then explains the functionality and truth tables of common logic gates like AND, OR, NOT. It also covers universal gates such as NAND and NOR. Finally, it describes exclusive OR and exclusive NOR gates through their symbols and truth tables. The document serves to introduce the essential concepts of logic gates in digital circuits and electronics.

Electronics lec 10Mohamed Abd Elghaffar

Digital electronics labswatymanoja

The document describes experiments conducted in a digital electronics lab to study and implement various logic gates and digital circuits. It includes summaries of experiments to study logic gates and verify their truth tables, design adders and subtractors using logic gates, and design various code converters including binary to gray, gray to binary, BCD to excess-3, and excess-3 to BCD. The document provides circuit diagrams, truth tables, and procedures for designing and verifying the operation of each digital circuit using logic gates.

De lab manualNaga Rajan

Logic gatesSchool of Design Engineering Fashion & Technology (DEFT), University of Wales, Newport

K-Map, Logic Gates.pdf .happycocoman

- Logic gates are fundamental building blocks of digital circuits that operate on binary inputs and produce binary outputs. Common logic gates include AND, OR, NOT, NAND, and NOR. - Combinational circuits are logic circuits whose outputs depend only on the present inputs. Sequential circuits are logic circuits whose outputs depend on both the present inputs and past outputs. - Karnaugh maps are a method for simplifying Boolean expressions by grouping adjacent 1s in a truth table representation. They allow visualizing simplifications that minimize logic gates in a circuit.

Deld lab manualVivek Kumar Sinha

Logic Gates - R.D.SivakumarSivakumar R D .

This document provides an introduction to logic gates. It defines logic gates as physical devices that implement Boolean functions, taking binary inputs of 0 and 1 and producing a single output. It then describes the functionality and truth tables of common logic gates including AND, OR, NOT, NAND, NOR, XOR and XNOR gates. It notes that NAND and NOR gates are universal in that they can be used to implement all other logic gates.

Logic gates and Boolean Algebra_VSGVaibhavGalbale1

Experiment write-vhdl-code-for-realize-all-logic-gatesRicardo Castro

Logic gatesrevised.pptDevanDev7

This document discusses digital logic gates and Boolean algebra. It defines the objectives as performing basic logic operations, describing AND, NAND, OR and NOR gates using truth tables, writing Boolean expressions, and implementing logic circuits. It explains Boolean constants and variables, the three basic logic operations (OR, AND, NOT), logic gates and their truth tables, gate IC numbers, and gives examples of implementing Boolean expressions as logic circuits.

combinational-circuit____gates_456788 (2).docxAjanya5

PLASyed Saeed

This document discusses programmable logic arrays (PLAs) and provides examples of implementing logic functions using a PLA. It defines a PLA as having programmable AND gates followed by programmable OR gates, making it well-suited for implementing sums-of-products logic functions. The document includes the structure of a PLA, the procedure for implementation, and provides four examples showing the logic diagrams and programming tables for PLAs implementing different logic functions with various numbers of inputs, outputs, and product terms.

Programmable Logic Array(PLA), digital circuits warda aziz

Hardware combinationalDefri Tan

Digital Logic & Computer Architecture Practical Book by Yasir Ahmed KhanYasir Khan

Here are the circuit designs and truth tables for the given Boolean expressions: 1. F = (a.b) (b'+c) Circuit: [CIRCUIT DIAGRAM OF GIVEN BOOLEAN EXPRESSION] Truth Table: [TRUTH TABLE OF GIVEN BOOLEAN EXPRESSION] 2. F = a + b'c Circuit: [CIRCUIT DIAGRAM OF GIVEN BOOLEAN EXPRESSION] Truth Table: [TRUTH TABLE OF GIVEN BOOLEAN EXPRESSION] Please let me know if you need any clarification or have additional questions!

logic circuits_walla2_c++_download_Welcome.pdfyyu8u

Logic gateNazim Naeem

logic gates.pptxaravind649229

CseAarti Masal

digital electronics .pptxAjaykumar967485

Electronics lec 10Mohamed Abd Elghaffar

Digital electronics labswatymanoja

De lab manualNaga Rajan

Logic gatesSchool of Design Engineering Fashion & Technology (DEFT), University of Wales, Newport

K-Map, Logic Gates.pdf .happycocoman

Deld lab manualVivek Kumar Sinha

Logic Gates - R.D.SivakumarSivakumar R D .

Logic gates and Boolean Algebra_VSGVaibhavGalbale1

Experiment write-vhdl-code-for-realize-all-logic-gatesRicardo Castro

Logic gatesrevised.pptDevanDev7

combinational-circuit____gates_456788 (2).docxAjanya5

PLASyed Saeed

Programmable Logic Array(PLA), digital circuits warda aziz

Hardware combinationalDefri Tan

Digital Logic & Computer Architecture Practical Book by Yasir Ahmed KhanYasir Khan

Recently uploaded (20)

MAQUINARIA MINAS CEMA 6th Edition (1).pdfssuser562df4

DT REPORT by Tech titan GROUP to introduce the subject design ThinkingDhruvChotaliya2

Artificial Intelligence (AI) basics.pptxaditichinar

introduction to machine learining for beginersJoydebSheet

Data Structures_Searching and Sorting.pptxRushaliDeshmukh2

Gas Power Plant for Power Generation SystemJourneyWithMe1

BCS401 ADA Second IA Test Question Bank.pdfVENKATESHBHAT25

Unit III.pptx IT3401 web essentials presentatiolakshitakumar291

Degree_of_Automation.pdf for Instrumentation and industrial specialistshreyabhosale19

Dust Suppressants: A Sustainable Approach to Dust Pollution ControlJanapriya Roy

This journal explores the growing field of bio-organic dust suppressants as a sustainable solution to dust pollution. It reviews the working principles of dust suppression, key performance indicators, and the latest research on using natural materials like polysaccharides, lignin, proteins, and agricultural wastes. It also highlights current challenges and future directions to enhance the durability, cost-effectiveness, and environmental safety of bio-based dust control technologies. A valuable reference for researchers, environmental engineers, and industry professionals seeking eco-friendly dust management solutions. Dust pollution, whether natural or anthropogenic, poses significant threats to both the environment and public health. Effective dust suppression technologies are essential in mitigating airborne particulate matter, especially in industrial, mining, and construction settings. Recently, bio-organic materials have emerged as promising raw materials for eco-friendly dust suppressants. This paper explores the working principles of dust suppressants, key performance evaluation indices, and the current progress in developing bio-based dust control agents using polysaccharides, lignin, proteins, microorganisms, and agricultural or forestry waste. It also discusses existing challenges and future research directions for enhancing the efficiency and applicability of bio-organic dust suppressants. Working Principles of Dust Suppressants Dust suppressants operate primarily through three interrelated mechanisms: wetting, coagulation, and consolidation. Wetting: This mechanism involves the application of dust suppressants to reduce the surface tension of water, allowing it to penetrate and coat dust particles. This increases the weight and cohesion of the particles, causing them to settle quickly. Surfactants and hygroscopic agents are commonly used in this approach. Coagulation: Dust particles are brought together to form larger aggregates through electrostatic interactions or binding agents, which helps in accelerating their settling. Consolidation: A more long-term effect where the suppressant forms a crust or mesh-like structure over the dust-prone surface, physically stabilizing it and preventing re-entrainment of particles by wind or vehicle movement. Bio-Organic Materials in Dust Suppressants The shift toward natural, renewable, and biodegradable components has led to extensive research on the use of various bio-organic substances, including: Polysaccharides: Starch, cellulose derivatives, and chitosan can form gels or films that stabilize surfaces. Lignin: A byproduct of the paper industry, lignin offers strong binding capacity and is naturally water-resistant. Proteins: Derived from agricultural waste, proteins like casein and soy protein can enhance binding and wetting. Microorganisms: Certain bacteria and fungi can produce biofilms or exopolysaccharides that trap dust particles. Agricultural and Forestry Wastes: Residues su

Elevate Your WorkflowNickHuld

Machine learning project on employee attrition detection using (2).pptxrajeswari89780

Building Security Systems in Architecture.pdfrabiaatif2

Building security systems are essential for protecting people, property, and assets within a structure. These systems include a range of technologies and strategies such as surveillance cameras (CCTV), access control systems, alarm systems, security lighting, and motion detectors. Modern security solutions often integrate smart technology, allowing remote monitoring and real-time alerts through mobile devices. Access control systems, like key cards or biometric scanners, ensure that only authorized individuals can enter certain areas, enhancing both safety and privacy. Alarm systems, whether triggered by unauthorized entry, fire, or environmental hazards, play a critical role in emergency response. Additionally, video surveillance acts as both a deterrent and a tool for investigating incidents. An effective building security system is carefully planned during the design phase, taking into account the building's size, purpose, and potential risks. Ultimately, robust security systems are vital for ensuring peace of mind, protecting lives, and preserving valuable assets.

Avnet Silica's PCIM 2025 Highlights FlyerWillDavies22

RESORT MANAGEMENT AND RESERVATION SYSTEM PROJECT REPORT.Kamal Acharya

The project developers created a system entitled Resort Management and Reservation System; it will provide better management and monitoring of the services in every resort business, especially D’ Rock Resort. To accommodate those out-of-town guests who want to remain and utilize the resort's services, the proponents planned to automate the business procedures of the resort and implement the system. As a result, it aims to improve business profitability, lower expenses, and speed up the resort's transaction processing. The resort will now be able to serve those potential guests, especially during the high season. Using websites for faster transactions to reserve on your desired time and date is another step toward technological advancement. Customers don’t need to walk in and hold in line for several hours. There is no problem in converting a paper-based transaction online; it's just the system that will be used that will help the resort expand. Moreover, Gerard (2012) stated that “The flexible online information structure was developed as a tool for the reservation theory's two primary applications. Computer use is more efficient, accurate, and faster than a manual or present lifestyle of operation. Using a computer has a vital role in our daily life and the advantages of the devices we use.

Value Stream Mapping Worskshops for Intelligent Continuous SecurityMarc Hornbeek

Lecture 13 (Air and Noise Pollution and their Control) (1).pptxhuzaifabilalshams

Basic Principles for Electronics Studentscbdbizdev04

Level 1-Safety.pptx Presentation of Electrical SafetyJoseAlbertoCariasDel

Fort night presentation new0903 pdf.pdf.anuragmk56

MAQUINARIA MINAS CEMA 6th Edition (1).pdfssuser562df4

DT REPORT by Tech titan GROUP to introduce the subject design ThinkingDhruvChotaliya2

Artificial Intelligence (AI) basics.pptxaditichinar

introduction to machine learining for beginersJoydebSheet

Data Structures_Searching and Sorting.pptxRushaliDeshmukh2

Gas Power Plant for Power Generation SystemJourneyWithMe1

BCS401 ADA Second IA Test Question Bank.pdfVENKATESHBHAT25

Unit III.pptx IT3401 web essentials presentatiolakshitakumar291

Degree_of_Automation.pdf for Instrumentation and industrial specialistshreyabhosale19

Dust Suppressants: A Sustainable Approach to Dust Pollution ControlJanapriya Roy

Elevate Your WorkflowNickHuld

Machine learning project on employee attrition detection using (2).pptxrajeswari89780

Building Security Systems in Architecture.pdfrabiaatif2

Avnet Silica's PCIM 2025 Highlights FlyerWillDavies22

RESORT MANAGEMENT AND RESERVATION SYSTEM PROJECT REPORT.Kamal Acharya

Value Stream Mapping Worskshops for Intelligent Continuous SecurityMarc Hornbeek

Lecture 13 (Air and Noise Pollution and their Control) (1).pptxhuzaifabilalshams

Basic Principles for Electronics Studentscbdbizdev04

Level 1-Safety.pptx Presentation of Electrical SafetyJoseAlbertoCariasDel

Fort night presentation new0903 pdf.pdf.anuragmk56

Logic gates and its realization

1. LOGIC GATES  Logic gates are the basic building blocks of any digital system.  It is an electronic circuit having one or more than one input and only one output.  The relationship between the input and the output is based on a certain logic. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 1

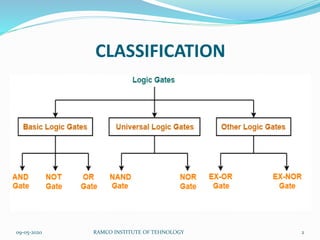
2. CLASSIFICATION 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 2

3. SYMBOLS 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 3

4. BASIC LOGIC GATES 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 4

5. AND GATE  The output of AND gate is high (‘1’) if all of its inputs are high (‘1’).  The output of AND gate is low (‘0’) if any one of its inputs is low (‘0’). 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 5

6. LOGIC SYMBOL 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 6

7. TIMING DIAGRAM 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 7

8. TRUTH TABLE A B Y = A.B 0 0 0 0 1 0 1 0 0 1 1 1 A B C Y = A.B.C 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 8

9. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 9

10. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 10

11. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 11

12. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 12

13. OR GATE  The output of OR gate is high (‘1’) if any one of its inputs is high (‘1’).  The output of OR gate is low (‘0’) if all of its inputs are low (‘0’). 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 13

14. LOGIC SYMBOL 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 14

15. TIMING DIAGRAM 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 15

16. TRUTH TABLE A B Y = A+B 0 0 0 0 1 1 1 0 1 1 1 1 A B C Y = A+B+C 0 0 0 0 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 1 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 16

17. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 17

18. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 18

19. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 19

20. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 20

21. NOT GATE  The output of NOT gate is high (‘1’) if its input is low (‘0’).  The output of NOT gate is low (‘0’) if its input is high (‘1’).  It is clear that NOT gate simply inverts the given input.  Since NOT gate simply inverts the given input, therefore it is also known as Inverter Gate. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 21

22. LOGIC SYMBOL 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 22

23. TIMING DIAGRAM 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 23

24. TRUTH TABLE A Y = A’ 0 1 1 0 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 24

25. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 25

26. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 26

27. UNIVERSAL LOGIC GATES 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 27

28. NAND GATE  A NAND Gate is constructed by connecting a NOT Gate at the output terminal of the AND Gate.  The output of NAND gate is high (‘1’) if at least one of its inputs is low (‘0’).  The output of NAND gate is low (‘0’) if all of its inputs are high (‘1’). 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 28

29. LOGIC SYMBOL 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 29

30. TIMING DIAGRAM 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 30

31. TRUTH TABLE A B Y = (A.B)’ 0 0 1 0 1 1 1 0 1 1 1 0 A B C Y = (A.B.C)’ 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 0 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 31

32. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 32

33. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 33

34. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 34

35. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 35

36. NOR GATE  A NOR Gate is constructed by connecting a NOT Gate at the output terminal of the OR Gate.  The output of OR gate is high (‘1’) if all of its inputs are low (‘0’).  The output of OR gate is low (‘0’) if any of its inputs is high (‘1’). 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 36

37. LOGIC SYMBOL 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 37

38. TIMING DIAGRAM 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 38

39. TRUTH TABLE A B Y = (A+B)’ 0 0 1 0 1 0 1 0 0 1 1 0 A B C Y = (A+B+C)’ 0 0 0 1 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 0 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 39

40. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 40

41. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 41

42. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 42

43. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 43

44. OTHER LOGIC GATES 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 44

45. EXOR GATE  The logic gate which gives high output (i.e., 1) if either input A or input B but not both are high (i.e. 1) is called exclusive OR gate or the XOR gate.  It may be noted that if both the inputs of the XOR gate are high, then the output is low (i.e., 0). 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 45

46. LOGIC SYMBOL 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 46

47. TRUTH TABLE A B Y = A ⊕ B 0 0 0 0 1 1 1 0 1 1 1 0 A B C Y = A ⊕ B ⊕ C 0 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 47

48. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 48

49. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 49

50. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 50

51. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 51

52. EXNOR GATE  The logic function implemented by a 2-input Ex-NOR gate is given as “when both A AND B are the SAME” will give an output at Q.  In general, an Exclusive-NOR gate will give an output value of logic “1” ONLY when there are an EVEN number of 1’s on the inputs to the gate (the inverse of the Ex-OR gate) except when all its inputs are “LOW”. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 52

53. LOGIC SYMBOL 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 53

54. TRUTH TABLE A B Y = (A ⊕ B)’ 0 0 1 0 1 0 1 0 0 1 1 1 A B C Y = (A ⊕ B ⊕ C)’ 0 0 0 1 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 0 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 54

55. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 55

56. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 56

57. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 57

58. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 58

59. LOGIC GATES and THEIR ICs IC NUMBER NAME OF THE GATE 7400 NAND 7402 NOR 7404 NOT 7408 AND 7432 OR 7486 EXOR/ XOR/ EOR 74266 EXNOR/ XNOR/ ENOR 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 59

60. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 60

61. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 61

62. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 62

63. 09-05-2020 RAMCO INSTITUTE OF TEHNOLOGY 63

Logic gates and its realization

Recommended

More Related Content

What's hot (20)

Similar to Logic gates and its realization (20)

Recently uploaded (20)

Logic gates and its realization