Low Complexity Regularization of Inverse Problems

Low Complexity
Regularization of
Inverse Problems
Gabriel Peyré

Joint works with:
Samuel Vaiter Jalal Fadili
Charles Dossal
Mohammad Golbabaee

VISI
www.numerical-tours.com

N

Overview

• Compressed Sensing and Inverse Problems

• Convex Regularization with Gauges

• Performance Guarantees

Single Pixel Camera (Rice)
x0
˜

x0
˜

y[i] = hx0 , 'i i

P measures

N micro-mirrors

x0
˜

y[i] = hx0 , 'i i

P measures

P/N = 1

N micro-mirrors

P/N = 0.16

P/N = 0.02

CS Hardware Model
˜
CS is about designing hardware: input signals f

L2 (R2 ).

Physical hardware resolution limit: target resolution f
2

x0 2 L
˜

array
resolution
CS hardware

x0 2 R

N

micro

mirrors

RN .

y 2 RP

CS Hardware Model
˜
CS is about designing hardware: input signals f

L2 (R2 ).

Physical hardware resolution limit: target resolution f

x0 2 L
˜

array
resolution

x0 2 R

N

micro

mirrors

y 2 RP

CS hardware

,
,
...

2

RN .

,

Operator
x0

Inverse Problems
Recovering x0 RN from noisy observations
y = x 0 + w 2 RP

Inverse Problems
Recovering x0 RN from noisy observations
y = x 0 + w 2 RP

Examples: Inpainting, super-resolution, compressed-sensing

x0

x0

Inverse Problem Regularization
Observations: y = x0 + w 2 RP .
Estimator: x(y) depends only on

observations y
parameter


observations y
parameter

Example: variational methods
1
x(y) 2 argmin ||y
x||2 + J(x)
x2RN 2
Data ﬁdelity Regularity


observations y
parameter

Example: variational methods
1
x(y) 2 argmin ||y
x||2 + J(x)
x2RN 2
Data ﬁdelity Regularity

Performance analysis:
! Criteria on (x0 , ||w||, ) to ensure

L2 stability ||x(y) x0 || = O(||w||)
Model stability (e.g. spikes location)

Union of Linear Models for Data Processing
Union of models: T 2 T linear spaces.
Synthesis
sparsity:
T

Coe cients x

Image

x

Synthesis
sparsity:

Structured
sparsity:

T

Coe cients x

Image

x

Synthesis
sparsity:

Structured
sparsity:

T

Coe cients x

Image

x

D

Analysis
sparsity:
Image x

Gradient D⇤ x

Synthesis
sparsity:

Structured
sparsity:

T

Coe cients x

Analysis
sparsity:

Image

x

D

Low-rank:

Image x

Gradient D⇤ x

S1,·

Multi-spectral imaging:
Pr
xi,· = j=1 Ai,j Sj,·

S2,·

x

S3,·

Gauges for Union of Linear Models
Gauge:

J :R

N

!R

+

Convex
8 ↵ 2 R+ , J(↵x) = ↵J(x)

Gauge:

J :R

N

!R

+

Convex
8 ↵ 2 R+ , J(↵x) = ↵J(x)

Piecewise regular ball , Union of linear models (T )T 2T

x
J(x) = ||x||1 T
T = sparse
vectors

Gauge:

J :R

N

!R

+

Convex
8 ↵ 2 R+ , J(↵x) = ↵J(x)


T0

x0

x

J(x) = ||x||1 T
T = sparse
vectors

Gauge:

J :R

N

!R

Convex
8 ↵ 2 R+ , J(↵x) = ↵J(x)

+


T
T0

x0

x

J(x) = ||x||1 T
T = sparse
vectors

x

T0

x
|x1 |+||x2,3 ||

T = block
sparse
vectors

0

Gauge:

J :R

N

!R

Convex
8 ↵ 2 R+ , J(↵x) = ↵J(x)

+


T
T0

x0

x

J(x) = ||x||1 T
T = sparse
vectors

x
T

x
|x1 |+||x2,3 ||

T = block
sparse
vectors

0

x

0

J(x) = ||x||⇤

T = low-rank
matrices

Gauge:

J :R

N

!R

Convex
8 ↵ 2 R+ , J(↵x) = ↵J(x)

+


T
T0

x0

x

J(x) = ||x||1 T
T = sparse
vectors

T0

x
T

x
|x1 |+||x2,3 ||

T = block
sparse
vectors

0

x

x
x0

0

J(x) = ||x||⇤

T = low-rank
matrices

J(x) = ||x||1

T = antisparse
vectors

Subdifferentials and Models
@J(x) = {⌘ 8 y, J(y) > J(x)+h⌘, y

xi}

|x|

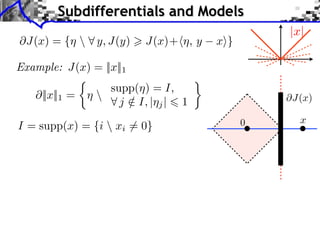
@J(x) = {⌘ 8 y, J(y) > J(x)+h⌘, y

|x|

xi}

Example: J(x) = ||x||1
⇢
supp(⌘) = I,
@||x||1 = ⌘
8 j 2 I, |⌘j | 6 1
/

I = supp(x) = {i xi 6= 0}

@J(x)
0

x

@J(x) = {⌘ 8 y, J(y) > J(x)+h⌘, y

|x|

xi}

⇢
supp(⌘) = I,
@||x||1 = ⌘
8 j 2 I, |⌘j | 6 1
/

I = supp(x) = {i xi 6= 0}
Tx = {⌘ supp(⌘) = I}

Deﬁnition:

Tx = VectHull(@J(x))?

@J(x)
0

x

Tx

@J(x) = {⌘ 8 y, J(y) > J(x)+h⌘, y

|x|

xi}

⇢
supp(⌘) = I,
@||x||1 = ⌘
8 j 2 I, |⌘j | 6 1
/

@J(x)
0

I = supp(x) = {i xi 6= 0}

Tx

Tx = {⌘ supp(⌘) = I}
ex = sign(x)

Deﬁnition:

Tx = VectHull(@J(x))?
⌘ 2 @J(x)

ex x

=)

ProjTx (⌘) = ex

Examples
`1 sparsity: J(x) = ||x||1
ex = sign(x)

x

@J(x)

x

0

Tx = {z supp(z) ⇢ supp(x)}

Examples
ex = sign(x)

P
Structured sparsity: J(x) = b ||xb ||
N (a) = a/||a||
ex = (N (xb ))b2B

x

@J(x)

x

0

x

@J(x)

x

0

Examples
ex = sign(x)

P
N (a) = a/||a||
ex = (N (xb ))b2B
Nuclear norm: J(x) = ||x||⇤

ex = U V

x

@J(x)

x

0

⇤

x

x = U ⇤V ⇤
SVD:

⇤
Tx = {z U? zV? = 0}

@J(x)

x

0

x
@J(x)

Examples
ex = sign(x)

P
N (a) = a/||a||
ex = (N (xb ))b2B
Nuclear norm: J(x) = ||x||⇤

ex = U V

⇤

x = U ⇤V ⇤
SVD:

⇤
Tx = {z U? zV? = 0}

I = {i |xi | = ||x||1 }
Anti-sparsity: J(x) = ||x||1
Tx = {y yI / sign(xI )}
ex = |I| 1 sign(x)

x

@J(x)

x

0

x

@J(x)

@J(x)

x

0

x
@J(x)

x

x

0

Dual Certificate and L2 Stability
Noiseless recovery:

min J(x)

x= x0

(P0 )

x?

x=

x0

Noiseless recovery:

min J(x)

x= x0

(P0 )

Proposition:
x0 solution of (P0 ) () 9 ⌘ 2 D(x0 )

Dual certiﬁcates:

D(x0 ) = Im(

⇤

⌘

x?

) @J(x0 )

@J(x0 )
x=

x0

Noiseless recovery:

min J(x)

x= x0

(P0 )

Proposition:
x0 solution of (P0 ) () 9 ⌘ 2 D(x0 )

Dual certiﬁcates:
D(x0 ) = Im(
¯
Tight dual certiﬁcates: D(x0 ) = Im(

⇤

⌘

@J(x0 )

x?

) @J(x0 )
⇤
) ri(@J(x0 ))

x=

x0

Noiseless recovery:

min J(x)

x= x0

(P0 )

Proposition:
x0 solution of (P0 ) () 9 ⌘ 2 D(x0 )

Dual certiﬁcates:
D(x0 ) = Im(
¯
Theorem:
¯
If 9 ⌘ 2 D(x0 ), for

⌘

@J(x0 )

x?

x=

x0

⇤

) @J(x0 )
⇤
) ri(@J(x0 ))
[Fadili et al. 2013]

⇠ ||w|| one has ||x?

x0 || = O(||w||)

Noiseless recovery:

min J(x)

x= x0

(P0 )

Proposition:
x0 solution of (P0 ) () 9 ⌘ 2 D(x0 )

Dual certiﬁcates:
D(x0 ) = Im(
¯
Theorem:
¯
If 9 ⌘ 2 D(x0 ), for

⌘

@J(x0 )

x?

x=

x0

⇤

) @J(x0 )
⇤
) ri(@J(x0 ))
[Fadili et al. 2013]

⇠ ||w|| one has ||x?

x0 || = O(||w||)

[Grassmair, Haltmeier, Scherzer 2010]: J = || · ||1 .
[Grassmair 2012]: J(x? x0 ) = O(||w||).

Compressed Sensing Setting
Random matrix:

2 RP ⇥N ,

i,j

⇠ N (0, 1), i.i.d.

Random matrix:

2 RP ⇥N ,

Sparse vectors: J = || · ||1 .

Theorem: Let s = ||x0 ||0 . If

i,j

⇠ N (0, 1), i.i.d.

[Rudelson, Vershynin 2006]
[Chandrasekaran et al. 2011]

P > 2s log (N/s)
¯
Then 9⌘ 2 D(x0 ) with high probability on

.

Random matrix:

2 RP ⇥N ,



i,j

⇠ N (0, 1), i.i.d.


P > 2s log (N/s)
¯

Low-rank matrices: J = || · ||⇤ .

Theorem: Let r = rank(x0 ). If

.


x0 2 RN1 ⇥N2

P > 3r(N1 + N2 r)
¯

.

Random matrix:

2 RP ⇥N ,



i,j

⇠ N (0, 1), i.i.d.


P > 2s log (N/s)
¯

Low-rank matrices: J = || · ||⇤ .

Theorem: Let r = rank(x0 ). If

.


x0 2 RN1 ⇥N2

P > 3r(N1 + N2 r)
¯

! Similar results for || · ||1,2 , || · ||1 .

.

Minimal-norm Certificate
⌘ 2 D(x0 )

=)

⇢

⌘ = ⇤q
ProjT (⌘) = e

T = T x0
e = ex0

⌘ 2 D(x0 )

=)

⇢

⌘ = ⇤q
ProjT (⌘) = e

Minimal-norm pre-certiﬁcate: ⌘0 =

T = T x0
e = ex0

argmin
⌘=

⇤ q,⌘

T =e

||q||

⌘ 2 D(x0 )

=)

⇢

⌘ = ⇤q
ProjT (⌘) = e

Proposition:

One has

T = T x0
e = ex0

argmin
⌘=

⌘0 = (

⇤ q,⌘

+
T

T =e

)⇤ e

||q||

⌘ 2 D(x0 )

=)

⇢

⌘ = ⇤q
ProjT (⌘) = e


argmin
⌘=

One has

⌘0 = (

¯
If ⌘0 2 D(x0 ) and

⇤ q,⌘

+
T

T =e

||q||

)⇤ e

⇠ ||w||,

Proposition:
Theorem:

T = T x0
e = ex0

the unique solution x? of P (y) for y = x0 + w satisﬁes

Tx ? = T x 0

and ||x?

x0 || = O(||w||) [Vaiter et al. 2013]

⌘ 2 D(x0 )

=)

⇢

⌘ = ⇤q
ProjT (⌘) = e


argmin
⌘=

One has

⌘0 = (

¯
If ⌘0 2 D(x0 ) and

⇤ q,⌘

+
T

T =e

||q||

)⇤ e

⇠ ||w||,

Proposition:
Theorem:

T = T x0
e = ex0

the unique solution x? of P (y) for y = x0 + w satisﬁes

Tx ? = T x 0

and ||x?

x0 || = O(||w||) [Vaiter et al. 2013]

[Fuchs 2004]: J = || · ||1 .
[Vaiter et al. 2011]: J = ||D⇤ · ||1 .
[Bach 2008]: J = || · ||1,2 and J = || · ||⇤ .

Random matrix:

2 RP ⇥N ,



i,j

⇠ N (0, 1), i.i.d.
[Wainwright 2009]
[Dossal et al. 2011]

P > 2s log(N )

¯
Then ⌘0 2 D( x0 ) wi th hi g h prob a b i l i ty on
.

Random matrix:

2 RP ⇥N ,

i,j


⇠ N (0, 1), i.i.d.
[Wainwright 2009]


P > 2s log(N )

¯

Phase
transitions:

L2 stability
P ⇠ 2s log(N/s)

vs.

.

Model stability
P ⇠ 2s log(N )

Random matrix:

2 RP ⇥N ,

i,j


⇠ N (0, 1), i.i.d.
[Wainwright 2009]


P > 2s log(N )

¯

Phase
transitions:

L2 stability
P ⇠ 2s log(N/s)

vs.

.

Model stability

! Similar results for || · ||1,2 , || · ||⇤ , || · ||1 .

P ⇠ 2s log(N )

Random matrix:

2 RP ⇥N ,

i,j


⇠ N (0, 1), i.i.d.
[Wainwright 2009]


P > 2s log(N )

¯

Phase
transitions:

L2 stability
P ⇠ 2s log(N/s)

vs.

.

Model stability

! Similar results for || · ||1,2 , || · ||⇤ , || · ||1 .

P ⇠ 2s log(N )

! Not using RIP technics (non-uniform result on x0 ).

1-D Sparse Spikes Deconvolution
⇥x =

xi (·

i)

x0

i

J(x) = ||x||1

Increasing :
reduces correlation.
reduces resolution.

x0

1-D Sparse Spikes Deconvolution
⇥x =

xi (·

x0

i)

i

J(x) = ||x||1

Increasing :
reduces correlation.
reduces resolution.

x0

||⌘0,I c ||1
2

1
0

10

20

I = {j x0 (j) 6= 0}
||⌘0,I c ||1 < 1
()
¯
⌘0 2 D(x0 )
()
support recovery.

Conclusion
Gauges: encode linear models as singular points.

Conclusion

Performance measures

L2 error
model

di↵erent CS guarantees

Conclusion


L2 error
model


Speciﬁc certiﬁcate ⌘0 .

Conclusion


L2 error
model


Speciﬁc certiﬁcate ⌘0 .
Open problems:
– Approximate model recovery Tx? ⇡ Tx0 .
– CS performance with complicated gauges (e.g. TV).

Low Complexity Regularization of Inverse Problems

Recommended

More Related Content

What's hot (20)

Similar to Low Complexity Regularization of Inverse Problems (20)

More from Gabriel Peyré (14)

Recently uploaded (20)

Low Complexity Regularization of Inverse Problems