Mastering Greedy Algorithms: Optimizing Solutions for Efficiency"

Greedy algorithm is generally used to solve optimization problems.
Optimization problems
A problem that may have many feasible solutions.
Each solution has a value.
Optimization problem can be either maximization or minimization problems,
where in maximization problem, we wish to find a solution to maximize the
value and in the minimization problem, we wish to find a solution to minimize
the value.
There are a number of approaches to solve optimization problems. Some of
them are given below-
• Branch and Bound
• Greedy Method
• Dynamic Programming
Greedy Algorithm

Greedy Algorithm
Algorithm Greedy (a, n)
{
Solution : = 0;
for i = 0 to n do
{
x: = select(a);
if feasible(solution, x)
{
Solution: = union(solution , x)
}
return solution;
}
}

Greedy Method finds out of many options, but you have to choose the best
option.
Greedy Algorithm solves problems by making the best choice that seems best
at the particular moment.
A greedy algorithm works in phases. At each phase:
You take the best you can get right now, without regard for future consequences
You hope that by choosing a local optimum at each step, you will end up at a
global optimum
Greedy algorithms are simple and straightforward, and they take decisions on
the basis of information at hand without worrying about the effect these
decisions may have in the future.
They are easy to invent, easy to implement and most of the time quite
efficient.
Greedy Algorithm

Only a few optimization problems can be solved by the greedy method. Some of
them are given below-
Machine scheduling
Fractional Knapsack Problem
Minimum Spanning Tree
Huffman Code
Job Sequencing
Activity Selection Problem
Steps for achieving a Greedy Algorithm are:
Feasible: Here we check whether it satisfies all possible constraints or not, to obtain
at least one solution to our problems.
Local Optimal Choice: In this, the choice should be the optimum which is selected
from the currently available
Unalterable: Once the decision is made, at any subsequence step that option is not
altered.
Greedy Algorithm

Knapsack Problem using Greedy
method
Two main kinds of Knapsack Problems
0-1 Knapsack:
N items (can be the same or different)
Have only one of each
Must leave or take (i.e., 0-1) each item (ingots of gold)
DP works, greedy does not since items cannot be broken
Fractional Knapsack:
N items (can be the same or different)
Can take fractional part of each item (bags of gold dust)
Greedy works and DP algorithms work
6
Knapsack Problem using Greedy method

Greedy approach for Fractional
Knapsack Problem
Steps to solve the Fractional Problem:
• Calculate the ratio(value/weight) for each item.
• Sort all the items in decreasing order of the ratio.
• Initialize res =0, curr_cap = given_cap.
• Do the following for every item in the sorted order:
• If the weight of the current item is less than or equal to the remaining capacity,
then add the value of that item into the result
• Else add the current item as much as we can (fraction) and break out of the loop.
• Return res.
7
Given a set of items, each with a weight and a value/profit, determine a subset of
items to include in a collection so that the total weight is less than or equal to a given
limit and the total value/profit is as large as possible.

Knapsack Problem
Example: Consider 5 items along their respective weights and values: -
I = (I1,I2,I3,I4,I5)
w = (5, 10, 20, 30, 40)
v = (30, 20, 100, 90,160)
The capacity of knapsack W = 60
8
The greedy algorithm:
Step 1: Sort vi/wi into non-increasing order.
Step 2: Put the objects into the knapsack according to the sorted sequence as
possible as we can.

Knapsack Problem
Example: Consider 5 items along their respective weights and values: -
The capacity of knapsack W = 60
First, we choose the item Ii whose weight is 5.
Then choose item I3 whose weight is 20.
Now, the total weight of knapsack is 20 + 5 = 25
Now the next item is I5, and its weight is 40, but
we want only 35, so we chose the fractional part of it,
So, we arrange the value of V/W in decreasing order as given in table and this will be the
solution of given problem.
The algorithm uses sorting to sort the items which takes O(n×logn) time complexity and then
loops through each item which takes O(n).Hence summing up to a time complexity of
O(n×logn+n)=O(n×logn). If the items are already sorted, then it takes O(n) time complexity.
9
I I1 I2 I3 I4 I5
W 5 10 20 30 40
V 30 20 100 90 160
V/W 6 2 5 3 4
I I1 I3 I5 I4 I2
W 5 20 40 30 10
V 30 100 160 90 20
V/W 6 5 4 3 2

Find Minimum number of Coins
Suppose we want a change for M Rs. and we have an infinite supply of each of the
denominations in Indian currency, i.e., we have an infinite supply of {1, 2, 5, 10, 20,
50, 100, 500, 1000} valued coins/notes, what is the minimum number of coins
and/or notes needed to make the change?
Input: M = 70
Output: 2
We need a 50 Rs note and a 20 Rs note.
Input: V = 121
Output: 3
We need a 100 Rs note, a 20 Rs note and a 1 Rs coin.
10
Solution: Greedy Approach.

Suppose we want a change for M Rs. and we have an infinite supply of each of the
denominations in Indian currency, i.e., we have an infinite supply of {1, 2, 5, 10, 20, 50,
100, 500, 1000} valued coins/notes, what is the minimum number of coins and/or notes
needed to make the change?
Input: M = 70
Output: 2
We need a 50 Rs note and a 20 Rs note.
Input: V = 121
Output: 3
We need a 100 Rs note, a 20 Rs note and a 1 Rs coin.
11
Algorithm:
1. Sort the array of coins in decreasing order.
2. Initialize result as empty.
3. Find the largest denomination that is smaller than current
amount.
4. Add found denomination to result. Subtract value of found
denomination from amount.
5. If amount becomes 0, then print result.
6. Else repeat steps 3 and 4 for new value of V

Input: M = 11, Denominations = {9, 6, 5, 1}
The greedy approach will return denomination 9, 1, and 1
Output-3
But we can solve by taking 5 and 6. So, output will be 2.
12
Note: This approach may not work for all denominations. For example, it
doesn’t work for denominations {9, 6, 5, 1} and M = 11. The above approach
would print 9, 1 and 1. But we can use 2 denominations 5 and 6. For general
input, dynamic programming approach can be used:

Given an undirected and connected graph G (V, E), a spanning tree of the graph G
is a tree that spans G and is a subgraph of G.
• The cost of the spanning tree is the sum of the weights of all the edges in the
tree. There can be many spanning trees. Minimum spanning tree (MST) is the
spanning tree where the cost is minimum among all the spanning trees. There
also can be many minimum spanning trees.
• Minimum spanning tree has direct application in the design of networks. It is
used in approximating the travelling salesman problem. Other practical
applications are:
• Cluster Analysis
• Handwriting recognition
• Image segmentation

How many spanning tree will be possible for above graph?
Total number of vertices (V)=4
Total number of edges (e)= 4, Spanning tree can be created by taking v-1 edges out
of e edges.
So, there will be 4C3 spanning trees.
1 2
4 3
Suppose the above graph contain one more edge b/w 1 and 3. Then, above formula
will be modified as follows.
5C3 – a
Where, a is the number of cycles formed. For the above graph, a=2.
1 2
4 3

How many spanning tree will be possible for above graph?
There are two famous algorithms for finding the Minimum Spanning Tree:
• Kruskal’s Algorithm
• Prims Algorithm

Kruskal’s Algorithm
▪ Kruskal’s Algorithm builds the spanning tree by adding edges one by
one into a growing spanning tree. Kruskal's algorithm follows greedy
approach as in each iteration it finds an edge which has least weight
and add it to the growing spanning tree.
Algorithm Steps:
▪ Sort the graph edges in increasing order with respect to their
weights.
▪ Start adding edges to the MST from the edge with the smallest
weight.
▪ Only add edges which doesn't form a cycle, until (n - 1) edges
are used.
▪ Stop

Minimum spanning tree with total cost=
11
( = 1 + 2 + 3 + 5)

Time Complexity:
As we have to select min cost edge from the graph, so we can use min heap
as it gives min values. So, if all the edges are kept in the min heap, then
after deleting every time we get the smallest value. The time taken to
delete an element from min heap is O(log n). So, time to create spanning
tree for n edge will be-
O(nlog n)

Prims’s Algorithm
▪ Prim’s Algorithm also use Greedy approach to find the minimum spanning
tree. In Prim’s Algorithm we grow the spanning tree from a starting position.
Unlike an edge in Kruskal's, we add vertex to the growing spanning tree in
Prim's.
General Steps:
1. First, we have to initialize an MST with the randomly chosen vertex.
2. Now, we have to find all the edges which are connected to the
vertex(ces). From the edges found, select the minimum edge and
add it to the tree.
3. Repeat step 2 until the minimum spanning tree is formed.

Prims’s Algorithm
Algorithm Steps:
▪ Create a set mstSet that keeps track of vertices already included in
MST.
▪ Assign a key value to all vertices in the input graph. Initialize all key
values as INFINITE. Assign key value as 0 for the first vertex so that
it is picked first.
▪ While mstSet doesn’t include all vertices
▪ Pick a vertex u which is not there in mstSet and has minimum key
value.
▪ Include u to mstSet.
▪ Update the key value of all adjacent vertices of u. To update the key
values, iterate through all adjacent vertices. For every adjacent
vertex v, if the weight of edge u-v is less than the previous key value
of v, update it else keep it as it is

MST-PRIM(G, w, r)
1. for each u ∈ G.V
2. u.key ← ∞
3. u.π ← NIL
4. r.key ← 0
5. Q ← G.V ------ (Build_Heap)
6. while Q ≠ Ø
7. u ← EXTRACT-MIN(Q)
8. for each v ∈ G.Adjacent[u]
9. if v ∈ Q and w(u, v) < v.key
10. v.π ← u
11. v.key ← w(u, v)

Use Prim’s algorithm to find an MST in the following graph.
The state at the start of the algorithm:
In the above diagram, the red text is the key
values of the vertices (i.e., v.key) and the green
text is the predecessor vertex.

The state at the start of the algorithm:
In the above diagram, the red text is
the key values of the vertices (i.e.,
v.key) and the green text is the
predecessor vertex.
First the algorithm picks an arbitrary starting
vertex and updates its key value to 0.
Here we arbitrarily choose A as our starting
vertex.
Vertex A B C D E F
Key 0 ∞ ∞ ∞ ∞ ∞
Predecessor NIL NIL NIL NIL NIL NIL

First the algorithm picks an arbitrary starting
vertex and updates its key value to 0.
Here we arbitrarily choose A as our starting
vertex.
Then A is extracted from the queue, and the
keys of its neighbours are updated:
Vertex colours: Blue: current vertex,
green: vertices added to tree.
Vertex A B C D E F
Key 0 1 1 ∞ ∞ ∞
Predecessor NIL A A NIL NIL NIL

Then D is extracted from the queue Finally, F is extracted from the queue and the
algorithm is complete

MST-PRIM(G, w, r)
1. for each u ∈ G.V
2. u.key ← ∞
3. u.π ← NIL
4. r.key ← 0
5. Q ← G.V
6. while Q ≠ Ø
7. u ← EXTRACT-MIN(Q)
8. for each v ∈ G.Adjacent[u]
9. if v ∈ Q and w(u, v) < v.key
10. v.π ← u
11. v.key ← w(u, v)
i. The time complexity required for one call to
EXTRACT-MIN(Q) is O(log V) using a min
priority queue. The while loop at line 6 is
executing total V times. EXTRACT-MIN(Q) is
called V times. So, the complexity of EXTRACT-
MIN(Q) is O(V logV).
ii. The for loop at line 8 is executing total V times
as a vertex may be connected to remaining |V-1|
vertices in complete graph. The time required to
execute line 11 is O(log v) by using the
DECREASE_KEY operation on the min heap.
Line 11 also executes total V-1 times.
So, the total time required to execute line 11 is
O(|V|*|V-1|*logV) = O(V2 logV).
Total time complexity of MST-PRIM is the sum of all time complexities i.e., O((VlogV) + (V2 logV)
+ (V)+ V) .
The DECREASE_KEY operation will execute for number of edges which are connected to the
selected vertex. So, we can replace V2 by E. Where, E= V*(V-1)/2 in worst case.
O((VlogV) + (E logV) + (V)+ V) = O((V+E) logV) => O((V+E) logV), since |E| >= |V|.
V times

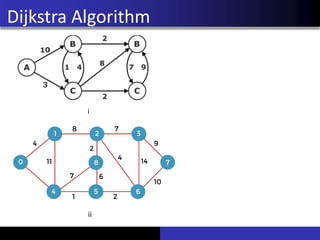
Construct the minimum spanning tree for the following graphs.
i
ii
iii

Dijkstra Algorithm
▪ Dijkstra algorithm is a single-source shortest path algorithm. Here,
single-source means that only one source is given, and we have to find
the shortest path from the source to all the vertices.
▪ It is minimization problem and can be solved by greedy method. It only
works on weighted graphs with positive weights.
▪ Dijkstra's algorithm allows us to find the shortest path between any two
vertices of a graph.
▪ It differs from the minimum spanning tree because the shortest distance
between two vertices might not include all the vertices of the graph.

Dijkstra Algorithm
▪ In Dijkstra, first select the starting vertex and set its cost =0. The cost of
remaining vertices will be set to ∞.
▪ Use the relaxation formula to update the cost of each vertex. The
relaxation formula is-
▪If(d[u]+c[u, v]< d[v] then
▪d[v]=d[u]+ c[u, v]
▪ Else
▪No change

Dijkstra Algorithm
Algorithm
1. Mark the source node with a current distance of 0 and the rest with
infinity.
2. Set the non-visited node with the smallest current distance as the
current node, lets say C.
3. For each neighbour N of the current node C: add the current distance
of C with the weight of the edge connecting C-N. If it is smaller than the
current distance of N, set it as the new current distance of N.
4. Mark the current node C as visited.
5. Go to step 2 if there are any nodes are unvisited.

Dijkstra Algorithm
Pseudo-code
Dijkstra (G, W, s) //uses priority queue Q
Initialize (G, s)
S ← φ
Q ← V [G] //Insert into Q (Min Heap)
while Q != φ
do u ← EXTRACT-MIN(Q) //deletes u from Q
S = S ∪ {u}
for each vertex v in Adj[u]
do RELAX (u, v, w) ← this is an implicit DECREASE KEY operation

Dijkstra Algorithm
Dijkstra Algorithm
Start with a weighted graph
Choose a starting vertex and assign infinity
path values to all other vertices
Go to each vertex and update its
path length
If the path length of the adjacent vertex is
lesser than new path length, don't update it

Dijkstra Algorithm
Dijkstra Algorithm
Avoid updating path lengths of
already visited vertices
After each iteration, we pick the unvisited
vertex with the least path length. So, we
choose 5 before 7
Notice how the rightmost vertex has its
path length updated twice
Repeat until all the vertices have been visited

Dijkstra Algorithm
Pseudo-code
Dijkstra (G, W, s) //uses priority queue Q
Initialize (G, s)
S ← φ
Q ← V [G] //Insert into Q -----
while Q != φ
do u ← EXTRACT-MIN(Q) //deletes u from Q ------
S = S ∪ {u}
for each vertex v in Adj[u]
do RELAX (u, v, w) ← DECREASE KEY operation
V times
V log V times
V log V times
----- V2 log V times

Dijkstra Algorithm
Dijkstra Algorithm Time Complexity-
The time complexity of Dijkstra's algorithm can be reduced to O((V+E)logV)
using adjacency list representation of the graph and a min-heap to store
the unvisited vertices, where E is the number of edges in the graph and V is
the number of vertices in the graph.
Time complexity = O((V+E)logV)

Problem Statement
In job sequencing problem, the objective is to find a sequence of
jobs, which is completed within their deadlines and gives maximum
profit.
Job Sequencing with Deadlines
The simple and brute-force solution for this problem is to generate all
the sequences of the given set of jobs and find the most optimal
sequence that maximizes the profit.
Time complexity of this solution would be O(2^n)
To optimize this algorithm, we can make use of a greedy approach that
produces an optimal result, which works by selecting the best and the
most profitable option available at the moment.

Job Sequencing with Deadlines: Algorithm
•Sort the jobs based on decreasing order of profit and find the largest
deadline
•Create a Gantt chart of maximum deadline size
•Iterate through the jobs and perform the following:
• Choose a Slot i if:
• Slot i isn’t previously selected.
• Slot i should be closest to its deadline
• i must be as maximum as possible
• If no such slot exists, ignore the job and continue.
Greedy approach

Job Sequencing with Deadlines: Example
JOBS DEADLINES PROFITS
Job 1 5 200
Job 2 3 180
Job 3 3 190
Job 4 2 300
Job 5 4 120
Job 6 2 100
In the table below, jobs with their profits and deadlines are given. What
would be the optimal sequencing of jobs which will give maximum profit?

Job 1 5 200
Job 2 3 180
Job 3 3 190
Job 4 2 300
Job 5 4 120
Job 6 2 100
In the table below, jobs with their profits
and deadlines are given. What would be
the optimal sequencing of jobs which will
give maximum profit?
Job 4 2 300
Job 1 5 200
Job 3 3 190
Job 2 3 180
Job 5 4 120
Job 6 2 100
Step 1:
Sort the jobs in decreasing order of their
profit.
Here we can see that value of the maximum
deadline is 5.

Step 2:
As maximum deadline is 5, so create a Gantt chart
of size 5
Step 3:
Now, pick the jobs one by one as presented in
step, 1, and place them on the Gantt chart as far
as possible from 0 and closest to its deadline.
We will pick Job 4. Its deadline is 2. So, placing
the job in the empty slot available just before the
deadline.
Job 4 2 300
Job 1 5 200
Job 3 3 190
Job 2 3 180
Job 5 4 120
Job 6 2 100

Step 4:
We will now pick Job 1. Its deadline is 5. So,
placing the job in the empty slot available just
before the deadline.
Step 5:
We will now pick Job 3. Its deadline is 3. So,
placing the job in the empty slot available just
before the deadline.
Step 6:
We will now pick Job 2. Its deadline is 3. Here
second and third slots are already filled. So,
place job 2 on the next available free slot i.e.,
first slot.
Job 4 2 300
Job 1 5 200
Job 3 3 190
Job 2 3 180
Job 5 4 120
Job 6 2 100

Step 7:
We will now pick Job 5. Its deadline is 4. Place the
job in the first empty slot before the deadline, i.e.,
fourth slot.
We will now pick Job 6. Its deadline is 2. Now we
need to place the job in the first empty slot
before the deadline. Since, no such slot is
available, hence Job 6 can not be completed.
So, the most optimal sequence of jobs to
maximize profit is Job 2, Job 4, Job 3, Job 5,
and Job 1.
And the maximum profit earned can be
calculated as:
Profit of Job 2 + Profit of Job 4 + Profit of Job 3 +
profit of Job 5 + profit of Job 1
180+300+190+120+200 = 990
Job 4 2 300
Job 1 5 200
Job 3 3 190
Job 2 3 180
Job 5 4 120
Job 6 2 100

Job Sequencing with Deadlines: Analysis
•Sort the jobs based on decreasing order of profit and find the largest deadline--- nlogn
•Create a Gantt chart of maximum deadline size -------------- K
•Iterate through the jobs and perform the following: ------------- n
• Choose a Slot i if:
• Slot i isn’t previously selected. ------------nxm
• Slot i should be closest to its deadline
• i must be as maximum as possible
• If no such slot exists, ignore the job and continue.
Since, size of the Gantt
chart array will be m and
max comparison to place
an item may be m and
for n jobs it will nxm
Time complexity= nlogn + n+ nxm +k
= nxm = O(n2) if n==m

Problem Statement
Given n number of sorted files of different lengths, the task is to find
the minimum computations done to reach the Optimal Merge Pattern.
Optimal Merge Pattern
Optimal merge pattern is a pattern that relates to the merging of two or
more sorted files in a single sorted file. This type of merging can be done
by the two-way merging method.
If we have two sorted files containing n and m records respectively then
they could be merged together, to obtain one sorted file in time O (n+m).

Let us consider the given files, f1, f2, f3, f4 and f5 with 20, 30, 10, 5 and 30 number
of elements, respectively.
If merge operations are performed according to the provided sequence, then
M1 = merge f1 and f2 => 20 + 30 = 50
M2 = merge M1 and f3 => 50 + 10 = 60
M3 = merge M2 and f4 => 60 + 5 = 65
M4 = merge M3 and f5 => 65 + 30 = 95
Hence, the total number of operations is
50 + 60 + 65 + 95 = 270
Now, the question arises is there any better solution?

Let us consider the given files, f1, f2, f3, f4 and f5 with 20, 30, 10, 5 and 30 number
of elements, respectively.
Sorting the numbers according to their size in an ascending order, we get the following
sequence −
f4, f3, f1, f2, f5
Hence, merge operations can be performed on this sequence
M1 = merge f4 and f3 => 5 + 10 = 15
M2 = merge M1 and f1 => 15 + 20 = 35
M3 = merge M2 and f2 => 35 + 30 = 65
M4 = merge M3 and f5 => 65 + 30 = 95
Therefore, the total number of operations is 15 + 35 + 65 + 95 = 210, which is less than
first one.
So, we need to find a merge pattern that can merge elements in the least number
of comparison.

Algorithm OPTIMAL_MERGE_PATTERNS(S) // S is set of sequences
Create min heap H from S
while H.length > 1 do
min1 ← minDel(H) // returns minimum element from H & delete it
min2 ← minDel(H)
NewNode.Data ← min1 + min2
NewNoode.LeftChild ← min1
NewNode.RightChild ← min2
Insert(NewNode, H)// Insert node NewNode in Heap
end
Optimal Merge Pattern: Greedy approach

Hence, the solution takes 15 + 35 + 60 + 95 = 205 number of comparisons.

Algorithm OPTIMAL_MERGE_PATTERNS(S) // S is set of sequences
Create min heap H from S
while H.length > 1 do
min1 ← minDel(H)
min2 ← minDel(H)
NewNode.Data ← min1 + min2
NewNoode.LeftChild ← min1
NewNode.RightChild ← min2
Insert(NewNode, H)
Complexity Analysis
The main loop in this algorithm is executed in n-1 times. In every iteration,
two delete minimum, and one insert operation is performed. Construction of
heap takes O(logn) time. The total running time of this algorithm is O(nlogn).
T(n) = (n – 1) * max(O(findmin), O(insert))

Complexity Analysis-
T(n) = (n – 1) * max(O(findmin), O(insert))
Case 1 : If list is sorted and stored in an array
O(findmin) = O(1) and O(insert) = O(n)
So, T(n) = (n – 1) * n = O(n2)
O(findmin) = O(1) and O(insert) = O(logn)
So, T(n) = (n – 1) * logn = O(nlogn)
Case 2 : List is represented as min-heap

Problem Statement
Huffman Coding is a technique of compressing data to reduce its size
without losing any of the details. It was first developed by David Huffman.
Huffman Coding is generally useful to compress the data in which there are
frequently occurring characters.
Huffman Coding
Suppose the string below is to be sent over a network.
As characters in computers are represented using ASCII code, which is
denoted by 8 bits in binary. There are a total of 15 characters in the
above string. Thus, a total of 8 * 15 = 120 bits are required to send this
string.
To reduce the size (compress) without losing any information, Huffman
coding is used. Huffman coding assign variable-length codes to input
characters.

Steps to build Huffman Tree-
1. Calculate the frequency of each character in the string.
2. Sort the characters in increasing order of the frequency. These are stored in a
priority queue Q using heap.
3. Make each unique character as a leaf node.
4. Create an empty node z. Assign the minimum frequency to the left child of z
and assign the second minimum frequency to the right child of z. Set the value
of the z as the sum of the above two minimum frequencies.
5. Remove these two minimum frequencies from Q and add the sum into the list
of frequencies (* denote the internal nodes in the figure above).
6. Insert node z into the tree.
7. Repeat steps 3 to 5 for all the characters.
8. For each non-leaf node, assign 0 to the left edge and 1 to the right edge.
Huffman Coding

Calculate the frequency of each character in the string.
Sort the characters in increasing order of the frequency. These are stored in
a priority queue Q.
Huffman Coding

Create an empty node z. Assign the minimum frequency to the left child of
z and assign the second minimum frequency to the right child of z. Set the
value of the z as the sum of the above two minimum frequencies.
Remove these two minimum frequencies from Q and add the sum into the
list of frequencies (* denote the internal nodes in the figure above).
Huffman Coding

Select two minimum elements from Q and add them in tree using the step
3.
Huffman Coding
For each non-leaf node, assign 0 to the left edge and 1 to the right edge

Assign 0 to the left edge and 1 to the right edge
Huffman Coding

For sending the string over a network, we have to send the tree as well as the
compressed-code. The total size is given by the table below.
Huffman Coding
Character Frequency Code Size
A 5 11 5*2 = 10
B 1 100 1*3 = 3
C 6 0 6*1 = 6
D 3 101 3*3 = 9
4 * 8 = 32 bits 15 bits 28 bits
Without encoding, the total size of the string was 120 bits. After encoding the
size is reduced to 32 + 15 + 28 = 75

create a priority queue Q using heap consisting of each unique character and its
frequency means a min heap is constructed for the frequencies.
for all the unique characters:
create a newNode
extract minimum value from Q and assign it to leftChild of newNode
extract next minimum value from Q and assign it to rightChild of newNode
calculate the sum of these two minimum values and assign it to the value of
newNode
insert this newNode into the tree and add the sum into the list of frequencies
return rootNode
Time complexity
Time Complexity is O(nlogn) because we are extracting minimum nodes 2*(n-1) times
and each time whenever a node is being extracted from the heap then a function
called heapify() is being called to rearrange the element according to their priority.
This function heapify() takes O(logn) time.
So, overall time= 2*(n-1) *log n = O(n log n)
Huffman Coding Complexity

Travelling Sales Person Problem
The travelling salesman problems abide by a salesman and a set of cities. The salesman has
to visit every one of the cities starting from a certain one (e.g., the hometown) and to return
to the same city. The challenge of the problem is that the travelling salesman needs to
minimize the total length of the trip.
Example: A newspaper agent daily drops the newspaper to the area assigned in such a
manner that he has to cover all the houses in the respective area with minimum travel
cost. Compute the minimum travel cost.
The area assigned to the agent where he has to drop the newspaper is shown in fig:
61

The TSP describes a scenario where a salesman is required to travel between
n cities. He wishes to travel to all locations exactly once and he must finish at
his starting point. The order in which the cities are visited is not important,
but he wishes to minimize the distance traveled.
The greedy algorithm goes as follows:
1. Sort all of the edges in the network.
2. Select the shortest edge and add it to our tour if it does not violate any of
the following conditions: there are no cycles in our tour with less than n
edges or increase the degree of any node (city) to more than 2.
3. If we have n edges in our tour stop, if not repeat step 2.
62

63
Find the optimal path for the following graph.
The weights of the edges of the graph is as
follows-
A <-> B = 2.4,
A <-> D =4.7,
A <-> C =6.8,
B <-> D = 5.1,
C <-> B =6,
C <-> D =5.9,

64

65

66

67
The Final answer is A -> B -> D -> C -> A = 2.4 + 5.1 +
5.9 + 6.8 = 20.2

68
Use algorithm and find the path
We can add the routes B <-> D, B <-> A and
C <-> D to our tour without problem
Path weight in ascending order
B <-> D = 2,
A <-> B = 4,
C <-> D =5,
A <-> D =6,
A <-> C =7,
C <-> B =8

69
Use algorithm and find the path
We can add the routes B <-> D, A <->
B and C <-> D to our tour without
problem
Path weight in ascending order
B <-> D = 2,
A <-> B = 4,
C <-> D =5,
A <-> D =6,
A <-> C =7,
C <-> B =8
We cannot add A <-> D to our tour as it
would create a cycle between the nodes A,
B and D and increase the order of node D to
3.
We therefore skip this edge and ultimately
add edge A <-> C to the tour.

70
Complexity: This algorithm searches for the local optima and optimizes the
local best solution to find the global optima.
• It begins by sorting all the edges and then selects the edge with the
minimum cost.
• It continuously selects the best next choices given a condition that no
loops are formed.
The computational complexity of the greedy algorithm is O(N2 log2(N)) and
there is no guarantee that a global optimum solution is found.

Mastering Greedy Algorithms: Optimizing Solutions for Efficiency"

Recommended

More Related Content

Similar to Mastering Greedy Algorithms: Optimizing Solutions for Efficiency" (20)

Recently uploaded (20)

Mastering Greedy Algorithms: Optimizing Solutions for Efficiency"