Math12 lesson5

GRAPHS OF TRIGONOMETRIC FUNCTIONS

GRAPH OF SINE FUNCTION: (y = sin x) Properties of Sine Function Graph:1. The graph crosses the x-axis at the initial point, endpoint and midpoint of a cycle. These points are called the zeros of the function.2. A maximum occurs midway between the first two zeros in the cycle, and a minimum occurs between the last two zeros. The maximum and the minimum values are determined by the amplitude.

Note:The graph of y = sin x is periodic meaning the curve repeats itself at a regular interval.

The graph of the function through one period is called cycle. The period of sine function is .

The amplitude represents the maximum variation of the curve from the x-axis. The amplitude of sine function is 1.Graph of y = sin x:yxo

GRAPH OF COSINE FUNCTION: (y = cos x) Properties of Cosine Function Graph:1. A maximum occurs at the initial point and the endpoint of the cycle. A minimum occurs midway in the cycle. The maximum and the minimum values are determined by the amplitude.2. The zeros of the function occur midway between the maximum and minimum.

Note:The graph of the cosine function has the same basic shape as y=sin x.

The graph is also periodic, with period , and it has also an amplitude of 1. Graph of y = cos x:yxo

Graph of y = a sin bxory = a cosbxFor y = a sin bxand y = a cosbx, the amplitude is . The period is . A negative sign before inverts the graph. Multiplying the sine or cosine function by a constant changes only the amplitude and causes vertical stretch or compression of the basic graph.The maximum and the minimum values of the graph y = a sin bxand y = a cosbxareand , respectively.

Graph of y = a sin b(x+c)+d ory = a cos b(x+c)+dFor y = a sin b(x+c)+d and y = a cos b(x+c)+d, the amplitude is and the period is . The phase shift (horizontal shift) is cunits to left if c > 0, and cunits to the right if c < 0. The vertical shift is d units upward if d > 0, and d units downward if d < 0.

EXAMPLE:Determine the amplitude, period, phase shift and vertical shift of each function. Sketch the graph over the interval .

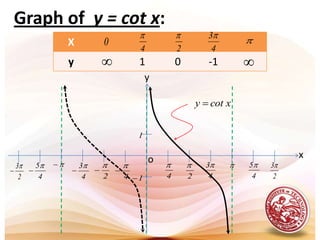
GRAPH OF TANGENT AND COTANGENT FUNCTIONS: The tangent function is discontinuous, since its graph has breaks. Asymptotes occur at these breaks. The amplitude is not defined because tanx increases or decreases without bound as x approaches the asymptotes. Since the tangent and cotangent functions are reciprocal functions, the value of cot xis undefined when tan x = 0, and it is zero when tan x is undefined.

Note:Tangent and cotangent functions has a period of .

The complete graph of tangent function is on the interval of using the fact that tangent is periodic with period .The complete graph of cotangent function is on the interval of . Graph of y = tan x:yxo

GRAPH OF SECANT AND COSECANT FUNCTIONS: The graph of secant and cosecant functions are discontinuous and has asymptotes since secant and cosecant functions are not defined when the values of cosine and sine are equal to zero, respectively.The amplitude is not defined because the graph increases or decreases without bound as x approaches the asymptotes.

Note:Secant and cosecant functions has a period of since both of them are the reciprocals of cosine and sine, respectively.

To graph the secant and cosecant functions, we get the values by using the reciprocal identities of and .

Math12 lesson5

More Related Content

What's hot (20)

Viewers also liked (15)

Similar to Math12 lesson5 (20)

More from dylanxclusive (9)

Recently uploaded (20)

Math12 lesson5

Editor's Notes