Meeting w4 chapter 2 part 2
Download as PPT, PDF•4 likes•9,799 views
The document discusses modeling of electrical and mechanical systems. It provides examples of modeling translational and rotational mechanical systems including springs, masses, dampers, motors, and gears. It derives transfer functions for various systems using equations of motion and Laplace transforms. One example shows modeling a closed-loop position control system with a motor, gears, load, and position feedback.
![cont. The net force F tending to accelerate the mass is F= Fs – FD, F = k ( Xi(t) – Xo(t) ) – ƒ Free Body Diagram, From N II, F = ma Laplace transform, Ms 2 Xo(s) = k[Xi(s) – Xo(s)] – BsXo(s) F=ma K(Xi-Xo) m ƒ](https://image.slidesharecdn.com/meetingw4-chapter2part2-110627223218-phpapp02/85/Meeting-w4-chapter-2-part-2-22-320.jpg)
Meeting w4 chapter 2 part 2
- 1. Chapter 2 – Analog Control System (cont.) Electrical Elements Modelling Mechanical Elements Modelling
- 2. 4. Electrical Elements Modelling
- 3. Example – RLC Network Determine the transfer function of the circuit. Solution: All initial conditions are zero. Assume the output is v c (t) . The network equations are
- 4. cont. Laplace transform the equation: Therefore,
- 5. Potentiometer A potentiometer is used to measure a linear or rotational displacement. Linear Rotational
- 6. Rotational Potentiometer The output voltage, Where Kp is the constant in V/rad. Where max is the maximum value for (t) . The Laplace transform of the equation is
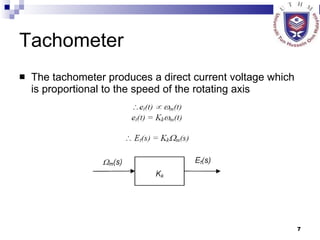
- 7. Tachometer The tachometer produces a direct current voltage which is proportional to the speed of the rotating axis
- 9. DC Motor Applications e.g. tape drive, disk drive, printer, CNC machines, and robots. The equivalent circuit for a dc motor is
- 10. DC Motor (cont.) Reduced block diagram The transfer function (consider TL(t) equals to zero)
- 11. Example 1 Problem : Find the transfer function, G(s) = VL(s)/V(s) . Solve the problem two ways – mesh analysis and nodal analysis. Show that the two methods yield the same result.
- 13. Now, writing the mesh equations, Nodal Analysis
- 14. 5. Mechanical Elements Modelling The motion of mechanical elements can be described in various dimensions, which are: 1. Translational. 2. Rotational. 3. Combination of both.
- 15. Translation The motion of translation is defined as a motion that takes place along or curved path. The variables that are used to describe translational motion are acceleration, velocity , and displacement .
- 17. Example 1 Find the transfer function for the spring-mass-damper system shown below. Solution: 1. Draw the free-body diagram of a system and assume the mass is traveling toward the right. Figure 2.4 a. Free-body diagram of mass, spring, and damper system; b. transformed free-body diagram
- 18. cont. From free-body diagram, write differential equation of motion using Newton’s Law. Thus we get; Laplace transform the equation: Find the transfer function:
- 19. Example 2 Find the transfer function, x o (s)/x i (s) for the spring-mass system. Solution: The ‘object’ of the above system is to force the mass (position x o (t)) to follow a command position x i (t). When the spring is compressed an amount ‘x’m, it produces a force ‘kx’ N ( Hooke’s Law ).
- 20. cont. When one end of the spring is forced to move an amount x i (t), the other end will move and the net compression in the spring will be x(t) = x i (t) – x o (t) So the force F acting on the mass are, From Newton’s second law of motion, F = ma Therefore, Transforming the equation:
- 21. Example 3 Find the transfer function for the spring-mass with viscous frictional damping. Solution: The friction force produced by the dash pot is proportional with velocity, which is; ƒ = viscous frictional constant N/ms-1
- 22. cont. The net force F tending to accelerate the mass is F= Fs – FD, F = k ( Xi(t) – Xo(t) ) – ƒ Free Body Diagram, From N II, F = ma Laplace transform, Ms 2 Xo(s) = k[Xi(s) – Xo(s)] – BsXo(s) F=ma K(Xi-Xo) m ƒ
- 23. Rotational Mechanical System The rotational motion can be defined as motion about a fixed axis. The extension of Newton’s Law of motion for rotational motion states that the algebraic sum of moments or torque about a fixed axis is equal to the product of the inertia and the angular acceleration about the axis where, J = Inertia T = Torque θ = Angular Displacement ω = Angular Velocity where Newton’s second law for rotational system are,
- 24. Modelling of Rotational Mechanical System
- 25. Example 1 Rotary Mechanical System
- 26. cont. The shaft has a stiffness k, which means, if the shaft is twisted through an angle θ, it will produce a torque kθ, where K – (Nm/rad). For system above the torque produce by flexible shaft are, Ts = K ( θ i (t)- θ o(t)) Nm The viscous frictional torque due to paddle Therefore the torque required to accelerating torque acting on the mass is Tr = Ts - TD
- 27. cont. From Newton’s second law for rotational system, Therefore, Transforming equation above, we get: Transfer function of system:
- 28. Example 2 Closed Loop Position Control System K s Load v a (t) Motor Amplifier Gears Load Handwheel Potentiometer K p Error Detector i o e(t) R L m (t)
- 29. cont. The objective of this system is to control the position of the mechanical load in according with the reference position. The operation of this system is as follows:- A pair of potentiometers acts as an error-measuring device. For input potentiometer, vi(t) = kpθi(t) For the output potentiometer, vo(t) = kpθo(t) The error signal, Ve(t) = Vi(t) – Vo(t) = kpθi(t) - kpθo(t) (1) This error signal are amplified by the amplifier with gain constant, Ks. Va(t) = K s Ve(t) (2)
- 30. cont. Transforming equations (1) and (2):- Ve(s) = Kpθi(s) - Kpθo(s) (3) By using the mathematical models developed previously for motor and gear the block diagram of the position control system is shown below:- + - B K t R+Ls i (s) + - K s n s o (s) K p V a (s) 1 J 1eq s+B 1eq T L (s) + -