Mining of time series data base using fuzzy neural information systems

 Introduction
The explosive growth in data and databases has generated
an urgent need for new techniques and tools that can
intelligently and automatically transform the processed
data into useful information and knowledge.
Consequently, data mining has become a research area
with increasing importance.
What is Data Mining ?
Data mining is nothing but the knowledge discovery in
databases, that means a process of nontrivial extraction of
implicit, previously unknown and potentially useful
information (such as knowledge rules, constraints,
regularities) from data in databases.

A data-mining algorithm constitutes a model, a
preference criterion, and a search algorithm. The
more common model functions in data mining
include classification, clustering, rule generation
and knowledge discovery
 What is Knowledge Discovery in Databases (KDD)?
Extraction of meaningful information from a large
database.

Data
Selection
Data
Compression
Data
formatting
Data Mining
KDD
Raw voltage
Data samples
Overall KDD block diagram

 What is time series data mining ?
A time series data is nothing but the data varies with time.
 Two types of time series data:
1. Periodic data
2. Non-stationary data
Examples of Non-stationary data:
 Seismic signal
 Power signal
 Speech signal
 Radar signal
 Biomedical signal and fluctuating data occurring in
business, financial markets including stocks, etc

 Existing Research work ?
 Objective of the thesis :
In this thesis is focused on the application of data
mining concepts to power network signal
disturbance time series, the approach is a general
one and can be applied to any time varying and non-
stationary data that arises in different fields of
science and engineering.

Data Mining Block diagram
Figure to be inserted from
published paper

Thus the main objective of the thesis is summarized as
1. Feature vector selection in data mining using
advanced signal processing techniques using Wavelet
transform and S-transform.
2. Developing a S-Transform based new hybrid K-
means and Particle Swarm Optimizer for data
clustering and classification in time series data mining.
Developing new Neural and Neuro-Fuzzy classifiers for
classification in data mining.
* Wavelet transform
* S-Transform

Fourier Transform
The Fourier Transform is one of the oldest and most
powerful tools in signal processing. This transform
maps the signal in time domain to a frequency domain.
The Fourier Transform of a signal is given as:
2
( ) ( ) i ft
Y f y t e dt



 
2
( ) ( ) i ft
y t Y f e df


 

Discrete version of FT is DFT of a time series of
length N is
21
0
1
[ ]
i nkTN
NT
k
n
Y y kT e
NT N
 

 
  

where T is the sampling interval.
Short Time Fourier Transform (STFT)
  2
, ( ) ( ) i ft
STFT f y t w t e dt
 



 

 Wavelet Transform and Multi-resolution
analysis
*
,( , ) ( ) ( )a bW a b y t t dt


 
where is any square integrable function, a is the scaling
parameter, b is the translation parameter and is the
dilation and translation of the mother wavelet.
, ( )a b t
( )y t
,
1
( )a b
t b
t
aa
 
 
  
 

Phase Corrected Wavelet: S-Transform
  2
( , ) ( ) , i ft
S f y t g t f e 
 



 
where the Gaussian modulation function g( , f) is given by
2
2
2
( , )
2
t
f
g f e 




with the spread parameter inversely proportional to the
frequency
1
f
 

The final expression becomes
2 2
( )
22
( , ) ( )
2
t f
i ftf
S f y t e e dt




 



 
To increase the frequency resolution, the spread of the Gaussian
window  is written as
f

 
and the generalized S-Transform is obtained as
2 2
2
( )
22
( , ) ( )
2
t f
i ftf
S f y t e e dt



 




 

Implementation of S-Transform (ST)
The computation of the S-Transform is efficiently implemented
using the convolution theorem and FFT. The following steps are
used for the computation of S-Transform:
1. Compute the DFT of the signal y(k) using FFT software
routine and shift spectrum Y[m] to Y[m+n].
2. Compute the Gaussian window function for
the required frequency n.
3. Compute the inverse Fourier Transform of the product of DFT
and Gaussian window function to give the ST matrix.
2 2 2 2
exp(-2π β m /n )

Comparison between DWT and S-Transform for
Analysis of Time Series Events
(a)Oscillatory transient (b) S-Transform output of oscillatory
transient
(a)
(b)

(a) Oscillatory transient (b) Level 4 detail coefficients (c) Level 3
detail coefficients (d) Level 2 detail coefficients (e) Level 1 detail
coefficients

(a) Swell (b) S-Transform output of voltage swell

(a) Swell (b) Level 4 detail coefficients (c) Level 3 detail coefficients
(d) Level 2 detail coefficients (e) Level 1 detail coefficients

Feature Extraction
Disturbances F1 F2 F3 F4 F5
Normal 1.002
Sag (60%) 0.593 0.053 .031 .0312 50.0
Swell (50%) 1.50 0.012
9
.076 .015 50
Momentary
Interruption (MI)
(5%)
0.0724 0.035 .019 .0350 50
Harmonics
(0% 3rd + 10% 5th)
1.0 0.033
9
.0556 .141 50
Sag with Harmonic
(60%)
0.601 .0228 .0408 .1139 50
Swell with Harmonic
(50%)
1.5 .0219 .079 .1155 50
Flicker (5 Hz, 4%) 0.987 .0168 .026 0.0186 55

Sag (60%) .591 .022 .039 .027 50
Swell (50%) 1.503 .012 .076 .029 50
Momentary
Interruption (MI)
.070 .0387 .0323 .044 50
Harmonics 1.032 .050 .064 0.25 50
Sag with Harmonic
(60%)
0.601 .0228 .0408 0.1139 50
Swell with Harmonic
(50%)
1.50 .0219 .079 .1155 50
Flicker (4%, 5 Hz) .998 .0209 .027 0.1159 55
Notch + harmonics .940 .1275 .0531 0.198 50
Spike + harmonics 1.072 .141 .066 .204 50
Transient
(low frequency)
1.021 0.1473 .0148 .0566 440

Table- 3: Effects of Window parameter α
Steady state variations Transient variations
Factor  F1 F2 F1 F2
0.4 0.602 0.0427 0.9877 0.1654
0.6 0.610 0.0236 0.9898 0.1650
0.8 0.621 0.01735 0.9911 0.1647
1 0.633 0.0145 0.9923 0.1623
1.2 0.645 0.0126 0.9927 0.1600

 Introduction
The goal of clustering is to identify the structure of an
unlabeled data set by objectively organizing data into
homogenous groups where the within-group-object
similarity is minimized and between the groups object-
dissimilarity is maximized. The clustering aims at
identifying and extracting significant groups in
underlying data.

Time series clustering using feature based approach.
Feature
Extraction (ST
or WT)
Clustering
algorithm
Time series ClustersFeatures
Model based Clustering
Discretization Modeling
Modeling Clustering
Model
parameters
Cluster
Centres
Coefficients of Residualsraw materials

K-Means Clustering
},...,2,1(},,...,2,1{, KjNizxd ji 


ji Cx
i
j
j Kjx
N
z ,...,2,1,
1
where zj is the jth cluster center. The necessary
condition of the minimum J is
where Nj is the number of points belonging to cluster
Cj.

PSO (Particle Swarm Optimization)
The aim of the PSO is to find the particle position that
results in the best evaluation of a given fitness (objective)
function. Each particle represents a position in Nd
dimensional space, and is “flown” through this multi-
dimensional search space, adjusting its position towards
both.
 the particle’s best position found thus far, and
 the best position in the neighborhood of that particle.
Each particle i maintains the following information:
 xi : The current position of the particle;
 vi : The current velocity of the particle ;
yi : The personal best position of the particle.

, , 1 1, , 2 2, ,
ˆ( 1) ( ) ( ) ( ( )) ( )( ( ) ( ))i k i k k i k k k i kv t wv t c r t y x t c r t y t x t      
( 1) ( ) ( 1)i i ix t x t v t   
where w is the inertia weight c1 and c2 are the acceleration
constants, , and k=1,…,Nd.1, ( )kr t 2, ( ) ~ (0,1),jr t U
PSO Clustering
In the context of clustering, a single particle represents the Nc cluster
centroid vectors. That is, each particle xi is constructed as follows:
1 1( ,..., ,..., )ci i j iNx m m m
where mi1 refers to the j-th cluster centroid vector of the i-th particle in cluster
Cij. The fitness of particles is easily measured as the quantization error,

1 ( , ) /p ij
Nc
j Z C p j ij
e
c
d z m C
J
N
  
  
 
where is the number of data vectors belonging to cluster Cij.ijC
gbest PSO Cluster Algorithm
1. Initialize each particle to contain Nc randomly selected cluster
centroids.
Calculate the Euclidean distance d(zp , mij) to all cluster
centroids Cij.
Using the above notation, the standard K-means algorithm is
summarized as
1. Randomly initialize the Nc cluster centroid vectors.

2. Repeat
(a) For each data vector, assign the vector to the class with
the closest centroid vector, where the distance to the centroid is
determined using
(b) Recalculate the cluster centroid vectors, using
1
p j
j p
Z Cj
m z
n  
 
until a stopping criterion is satisfied.
(ii) Assign zp to cluster Cij such that
(i)
 1,...,( , ) min ( , )cp ij c N p icd z m d z m 
(1)
(2)

(iii) Calculate the global best and local best positions
c) Update the global best and local best positions
d) Update the cluster centroids using equations (1) and (2).
where tmax is the maximum number of iterations.
Hybrid PSO Algorithm
It is based on the passive congregation and a kind of coordinated
aggregation observed in the swarms known as GPAC-PSO and
modifying it further to yield GPAC-Adaptive PSO or simply to be
known as GPAC-APSO.
The swarms of the enhanced GPAC is manipulated by the velocity
update
 1 1 2 2 3 3( 1) . ( ). ( ) . .( ( ) . .( ( )) . .( ( ))i i i i k i r iv t k w t v t c rand P S t c rand P S t c rand P S t       

where i = 1, 2,…, N; c1, c2, and c3 are the cognitive, social, and
passive congregation parameters, respectively; rand1, rand2, and
rand3 are random numbers uniformly distributed within [0,1]; Pi is
the best previous position of the ith particle; Pk is either the global
best position ever attained among all particles in the case of
enhanced GPAC and Pr is the position of passive congregator
(position of a randomly chosen particle-r).

 the quantization error
 the intra-cluster distances, i.e. the distance between
data vectors within a cluster, where the objective is to
minimize the intra-cluster distances;
 the inter-cluster distances, i.e. the distance between the
centroids of the clusters, where the objective is to
maximize the distance between clusters.
w=0.72 and c1=c2=1.49 to ensure good convergence.

(a) F1- F2 K-Means PSO
Cluster-4
Cluster-3
Cluster-1
Cluster-2
HYBRID PSO OUTPUT :
Cluster 1 Sag
Cluster 2: Swell
Cluster 3: Normal + harmonic
Cluster 4: Transient + Notch

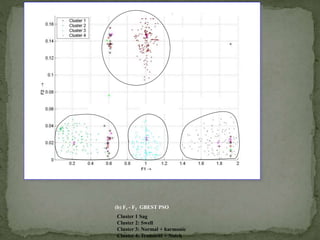
GBEST PSO OUTPUT
(b) F1 - F2 GBEST PSO
Cluster-1
Cluster-4
Cluster-3Cluster-2
GBEST PSO OUTPUT
Cluster 1 Sag
Cluster 2: Swell

(c) F1- F2 GPAC APSO
GPAC APSO OUTPUT
Cluster-4
Cluster-1
Cluster-3
Cluster-2
Cluster 1 Sag
Cluster 2: Swell

F1 - F2 Fitness Plots
GPAC APSO
PSO
K-Means
GBEST PSOGPAC APSO
K-Means
PSO
GPAC-APSO
GBEST PSO

The proposed method is very efficient and simple to
implement for clustering analysis when the number of
clusters is known a priori. The modified GPAC-PSO
known as GPAC-APSO is found to be more efficient and
has a quick convergence property in comparison to other
PSO variants.

The next step in this research is to transform the
visually distinguishable patterns to feature vectors
that can be used by classifiers such as neural
networks to automatically classify the
disturbances.

*
In order to improve the classification accuracy a novel neural
architecture comprising hybrid combinations of the radial basis
function neural network and a functional link network that provides
a more robust pattern recognizer for non-stationary time series data
is undertaken for detailed study.

Signal
S-transform
Feature
extraction
Neural
Network
Display recognized
patterns
PO
ST
PR
OC
ESS
I
NG
A Neural network architecture is used to test the efficacy
of the proposed method.

 
2
1


Q
j
ij xdE
)()1( kEk w  
where Q is the number of training samples and the
weights are updated as
where wE is the gradient with respect to weight, and  is
the momentum constant, and  is the learning rate.

It consists of a radial basis layer and a competitive layer.
FIGURE 4.3
TO INSERT

where
i number of input layers;
h number of hidden layers
j number of output layers;
k number of training examples;
Nk number of classification (clusters);
σ smoothing parameters (standard deviation), 0.1< σ <1
X input vector;
The algorithm of the inference output vector Y in the PNN is as
follows:
1
. and ,hy hy
j hj h j hj
h hj
net W H N W
N
  
max( ) then 1, else 0j k j j
k
net net Y Y  If

Euclidean distance between the vectors X and Xkj,
 
2
kj i kji
X X X X  
connection weight between the input layer X and the hidden layer
H;
is the connection weight between the hidden layer H and the output
layer Y.
xh
ihW
hy
hjW

We use RBFs with the random vector functional link nets
(RVFLNs) to obtain the powerful radial basis functional
link nets (RBFLNs).
As RBFNN represents a nonlinear model while the RBFLN
includes that nonlinear model as well as a linear model
(the direct lines from the input to output nodes) so that the
linear parts of a mapping do not need to be approximated
by the nonlinear model.

Radial Basis Functional Link Net (RBFLN)

For an input vector , the output of th output node produced by
an RBF is given by
  

 

11
11
)(
1 1
)(
2
)()()(
m
n
noj
m
i i
ctx
ij
m
i
m
n
nojiijj txwewtxwtwto
i


where is the center of the ‘i’ th hidden node, is the width
of the ‘i’th center, and is the total number of hidden
nodes.
If output of the hidden neurons, by vector notation
))t(....,),........t(),t(( tot 21
and weight vector for the hidden RBF units

)w,......,w,w(w mjj2j1j  and the weight vector for the linear units
)w,.......,w,w(w mjj2j1j

RBFLN output can be written as
j
T
jj wwo 
The sets of centers are trained with K-means clustering
approach, where the centers are initially defined as the first
training inputs that correspond to a specific class . The
Centroid vector is given by
 )c(x.,),........c(x),c(x)i(C mcc 210 
c

At each iteration , following a new input is presented,
the distance for each of the centers is denoted by
i )(ix
)i(jj c)i(x)i( 1 cm...,,.........2,1j where
The kth center is updated by the following equation:
)i()i(C)i(C kkk  1
k is chosen in such a way that it minimizes )(ij
)i(arg(min(k jThus
and is the learning rate.

The width associated with the k th center is adjusted as
2
1
1


aN
j
jkk )i(C)i(C
N
)i(
Where N is the number of hidden neurons.
Wavelet based Neural Classification Schemes
Method-1 (WT-1) was implemented using the thirteen level coiflet
5-wavelet decomposition. The de-noising step in Method-2(WT-2)
was omitted to test its effectiveness in noise. A hybrid DFT-DWT
fuzzy expert system approach known as Method-3 (WT-3) is also
considered in this paper for feature extraction and disturbance
pattern classification.

Distortionclassificationinwaveletdomain

Block diagram of classification algorithm

The important features obtained from the Fourier (DFT) and wavelet analysis
(DWT) for the non-stationary disturbance time series data are listed as follows:
1 Fundamental and harmonic components obtained from the Discrete
Fourier Transform of the time series signal data samples.
2. The phase angle shift of the disturbance time series with respect to
normal waveform Ln.
3. Number of peaks of the wavelet coefficients (Nn).
4. Energy of the wavelet coefficients (Ewn).
5. Oscillation number of missing voltage time series data.

The extracted features are then used with different types of
neural classifiers such as multilayered perceptron network,
probabilistic neural network, and proposed radial basis
functional link network for pattern classification, data
mining and subsequent knowledge discovery.

MLP Pure 30dB
Method WT-1 WT-2 ST WT-1 WT-2 ST
Oscillatory transient 95% 95% 90% 30% 90% 95%
Impulsive transient 100% 70% 95% 100% 65% 85%
Multiple notch 100% 85% 100% 90% 85% 100%
Voltage swell 100% 100% 100% 55% 95% 100%
Voltage sag 90% 80% 80% 60% 85% 96%
Interruption 100% 90% 100% 100% 95% 100%
Harmonics 100% 85% 90% 15% 80% 85%
Swell +
harmonics 100% 95% 100% 60% 95% 100%
Sag +harmonics 100% 80% 100% 25% 80% 100%
Average 98.33% 86.67% 95% 59.44% 85.56% %

RBFLN Pure 30dB
Oscillatory
transient 95% 95% 80% 45% 30% 90%
Impulsive
transient 100% 75% 100% 95% 65% 70%
Multiple notch 85% 85% 90% 85% 85% 95%
Voltage swell 100% 95% 90% 75% 95% 90%
Voltage sag 85% 85% 80% 80% 85% 70%
Interruption 100% 100% 100% 25% 100% 100%
Harmonics 100% 95% 90% 5% 80% 90%
Swell
+harmonics 100% 100% 100% 50% 100% 100%
Sag+harmonics 80% 85% 100% 55% 85% 100%

Oscillatory
transient 95% 95% 95% 35% 15% 80%
Impulsive
transient 100% 65% 95% 100% 70% 60%
Multiple notch 100% 85% 90% 90% 90% 95%
Voltage swell 100% 100% 90% 50% 100% 85%
Voltage sag 75% 85% 80% 35% 85% 75%
Interruption 100% 100% 100% 100% 100% 100%
Harmonics 95% 90% 90% 25% 85% 90%
Swell+
harmonics 85% 100% 100% 45% 100% 100%
Sag+harmonics 60% 80% 75% 45% 75% 70%
Average 90% 88.89% 90.56% 58.33% 80% 83.89%

Type of time
series data
Number of
disturbances
Number of class
correctly identified
WT-3 ST
Sag 100 99 92
Swell 100 100 96
Interruption 100 100 97
Harmonics 100 98 95
Switching
transients
100 95 90
Impulse 100 92 97
Flicker 100 99 96
Notch 100 100 94
Average 100% 97.87% 94.62%

Mining of time series data base using fuzzy neural information systems

Mining of time series data base using fuzzy neural information systems

Recommended

More Related Content

What's hot (18)

Similar to Mining of time series data base using fuzzy neural information systems (20)

More from Dr.MAYA NAYAK (8)

Recently uploaded (20)

Mining of time series data base using fuzzy neural information systems