Optimal power flow with distributed energy sources using whale optimization algorithm

International Journal of Electrical and Computer Engineering (IJECE)
Vol. 13, No. 5, October 2023, pp. 4835~4844
ISSN: 2088-8708, DOI: 10.11591/ijece.v13i5.pp4835-4844  4835
Journal homepage: http://ijece.iaescore.com
Optimal power flow with distributed energy sources using
whale optimization algorithm
TentuPapi Naidu1,2
, Ganapathy Balasubramanian3
, Bathina Venkateshwara Rao4
1
Department of Electrical and Electronics Engineering, Annamalai University, Chidambaram, India
2
Department of Electrical and Electronics Engineering, Lendi Institute of Engineering and Technology, Andhra Pradesh, India
3
Department of Electrical Engineering, Government College of Engineering, Tirunelveli, India
4
Department of Electrical and Electronics Engineering, V. R. Siddhartha Engineering College, Andhra Pradesh, India
Article Info ABSTRACT
Article history:
Received Nov 26, 2022
Revised Jan 17, 2023
Accepted Feb 4, 2023
Renewable energy generation is increasingly attractive since it is
non-polluting and viable. Recently, the technical and economic performance
of power system networks has been enhanced by integrating renewable
energy sources (RES). This work focuses on the size of solar and wind
production by replacing the thermal generation to decrease cost and losses
on a big electrical power system. The Weibull and Lognormal probability
density functions are used to calculate the deliverable power of wind and
solar energy, to be integrated into the power system. Due to the uncertain
and intermittent conditions of these sources, their integration complicates the
optimal power flow problem. This paper proposes an optimal power flow
(OPF) using the whale optimization algorithm (WOA), to solve for the
stochastic wind and solar power integrated power system. In this paper, the
ideal capacity of RES along with thermal generators has been determined by
considering total generation cost as an objective function. The proposed
methodology is tested on the IEEE-30 system to ensure its usefulness.
Obtained results show the effectiveness of WOA when compared with other
algorithms like non-dominated sorting genetic algorithm (NSGA-II), grey
wolf optimization (GWO) and particle swarm optimization-GWO (PSO-
GWO).
Keywords:
Fuel cost
Optimal power flow
Optimization
Solar power
Whale optimization algorithm
This is an open access article under the CC BY-SA license.
Corresponding Author:
Bathina Venkateshwara Rao
Department of Electrical and Electronics Engineering, V. R. Siddhartha Engineering College
Andhra Pradesh-520007, India
Email: drbvrao@vrsiddhartha.ac.in
1. INTRODUCTION
Proper planning is necessary for improved usage of resources already existing in the power system.
optimal power flow (OPF) has recently emerged as a popular issue for realizing the optimal planning of a
real-timesystemfunction is very much necessary for achieving operation and control of modern power
systems. Various objectives including power losses, emissions, and voltage stability are taken into account
for optimizing the variable regulation using OPF. Different traditional optimization strategies for tackling
OPF problems have been presented in the literature [1] and these procedures have occasionally failed to
provide the desired effects. This can be overcome employing by a heuristic approach and metaheuristic
methodology that take into account the randomization of controlled parameters. Various authors used a
variety of strategies to address the OPF problem, some of which are described below. Particle swarm
optimization (PSO) was used by [2] authors to solve the OPF. The PSO examined for IEEE thirty Bus test
case for reduced goal operation like voltage stability improvement, power loss and total fuel cost. In [3] grey

 ISSN: 2088-8708
Int J Elec & Comp Eng, Vol. 13, No. 5, October 2023: 4835-4844
4836
wolf optimizer (GWO) the differential evolution algorithms were proposed with voltage proficiency
enhancement and actual power loss minimization as goals. The suggested algorithm’s performance was
evaluated for IEEE test cases of 57- buses and 118-buses. An improved genetic algorithm (GA) technique,
[4] presents a linear adaptive genetic algorithm and It has tested for IEEE six and and 14-Bus systems. In [5],
gravity search method was utilized to solve the OPF issue to address transmission losses. It has been
examined on the Indiantwenty-four bus system. For tackling the OPF issue, the literature [6] suggested a
multi-objective glow-worm swarm optimization method. The moth-flame optimizer (MFO) approach was
utilized in this [7] to tackle the OPF problem. There are several objectives for improved management in
power systems, including emissions, active power losses, running costs, the collision of voltage, and stability.
This literature study presents several linear, nonlinear, and metaheuristic approaches available in literature
for power system networks. While power systems have been extensively modified in recent years, classic
optimization procedures have been reinstated. In this environment, optimum power flow is the most
important technical, adaptive, and economic instrument OPF. We compare different OPF methods to
considered objective function in this work. Finally, we will discuss some of the fundamental issues raised by
the new OPF method for the contemporary grid. For the OPF issue, Bhowmik and Chakraborty [8] suggested
a multi-objective non-dominated sorting GA II algorithm.
The objective function of increased voltage stability was this algorithm’s key contribution. The salp
swarm algorithm (SSA) was proposed in [9] for tackling the OPF issue. Jaya optimization method was
employed by the authors [10] to solve the OPF issue. The goal functions are reduced using this algorithm.
Samakpong et al. [11] used the random inertia weight particle swarm optimization (RANDIW-PSO)
technique for the OPF issue which was investigated for the IEEE thirty-nine bus system. In [12] presented a
cuckoo search strategy foraddressing the multi-objective OPF issue. In [13], [14], the whale optimization
method, a novel metaheuristic algorithm was utilized for handling structural design for a single goal and
restricted optimization problems. This approach emulates humpback whale social behavior.
Renewable energy sources (RES) such as solar and wind power with skill curves are used in large
power transmission systems based on the maximum power extraction principle [15], [16]. The solar
irradiance model [17], [18] and wind power model for the OPF [19], [20] are extensively discussed in this.
The costs of solar photovoltaic (PV) and wind turbine generators for the OPF with constraints, goals, and
fitness functions [21], [22]. Solar power’s active power must be limited. Active and reactive power control
objectives, as well as other objectives such as voltage stability, emission, costs, losses, and technical
parameters, are controlled for large bus systems and efficiently used in the optimal power flow problem [23],
[24]. Pandiarajan et al. discuss OPF problems in detail, with details on objectives, constraints, algorithms
used, and their outcomes in [25], [26]. Recently, most of the works are built on RES, and such mixed integer
linear programming and metaheuristic approaches are new with the goal of minimizing carbon emissions and
acting as an eco-friendly system [27].
Linear programming’s low suppleness and insufficient framework are primary limitations, therefore
we need seek for non-linear programming, which has more flexibility and platform access, but still requires a
specialized solution, thus metaheuristic optimization approaches are discovered to be more advantageous
[28]. Among these ideal approaches, the genetic algorithm is the easiest to create, has the most flexibility,
and is available on a variety of platforms, at the expense of a higher computational cost and comparably low
performance [29]. To address this, PSO can give superior speed, flexibility, platform access, and ease of
execution, but at a higher computational cost [30]. Mix-integer programming is a great deal method that has a
solution to the above concerns and is more flexible and ideal for electric car charging control, but it still
requires specific solvers and approaches and has a higher computational price for large scale dimensions
problems [31]. Modern meta-heuristic approaches, such as whale optimization algorithm (WOA) developed
by the previous authors, may overcome concerns such as computation cost and burden, as well as give more
flexibility, diverse platform access, and better performance, but parameter setup remains complex [32], [33].
The contribution of the work is to create a one-of-a-kind WOA for the MOOPF-WS challenge,
which incorporated solar PV, wind and thermal producers into the grid. Several probability density functions
(PDFs) were utilised to represent uncertainty in RES and load demand. To determine the non-dominated
ranks and densities of the solutions generated, WOA used rapid non-dominated sorting and crowding
distance approaches. Furthermore, the Pareto archive selection approach was used for non-dominated
solution distribution maintenance. For all discrete loading situations, the variable loading scenario has
significantly worse predicted performance characteristics than the constant loading case. This shown that
solving OPF under changing load conditions provides more flexible and effective generator scheduling than
under steady load conditions, resulting in lower anticipated performance profiles. Furthermore, employing
high voltage (HV) indicators, the multi-objective search group algorithms (MOSGA’s) performance was
compared to the non-dominated sorting genetic algorithm (NSGA-II), multi objective ant lion optimization
(MOALO), and WOA. The WOA beat the other three techniques in terms of convergence and diversity of

Int J Elec & Comp Eng ISSN: 2088-8708 
Optimal power flow with distributed energy sources using whale optimization algorithm (TentuPapi Naidu)
4837
Pareto optimum solutions in all cases. As a result, WOA could uncover the wider variety of non-dominated
solutions for all objective functions. when compared to major studies in the literature, WOA obtained higher
quality solutions in all similar circumstances. These demonstrated the WOA’s capabilities and proved its
capability in dealing with the MOOPF-WS challenge.
The WOA recently adopted to solve numerous power system challenges. It was driven to
demonstrate the WOA’s feasibility and efficacy in resolving the OPF problem. This work presents a WOA
strategy to resolvethe OPF issue on IEEE 30 Bus system, with three distinct objectives to demonstrate the
method’s superiority over GWO and PSO-GWO. The manuscript is organized as: section 2 describes the
determine optimal power flow and the modeling of RES units for optimal power flow is presented in
section 3. Section 4 presents the WOA, section 5 presents the results and anlysis for numerous objective
functions of the IEEE thirty bus system, followed by the 6 section conclusions.
2. DETERMINISTIC OPTIMAL POWER FLOW
2.1. Total generation cost minimization
Quadratic functions are utilized to represent the total generation cost function given in (1). The
thermalgenerating unit’s cost is determined by using (2). Wind generation cost is calculated with (3). The
generation cost of the solar units is determined by using (4).
𝐹 = 𝑓𝑡(𝑃𝑡) + 𝑓𝑤,𝑖(𝑃𝑤,𝑖) + 𝑓𝑠𝑜,𝑗(𝑃𝑠𝑜,𝑗) (1)
𝑓𝑡(𝑃𝑡) = (∑ ∑ (𝑎𝑖𝑃𝐺𝑖,ℎ
2
𝑁𝑔
𝑖=1
+
24
ℎ=1 𝑏𝑖𝑃𝐺𝑖,ℎ + 𝑐𝑖)) + |𝑑𝑖 𝑠𝑖𝑛( 𝑒𝑖(𝑃
𝐺𝑖,ℎ
𝑚𝑖𝑛𝐺𝑖,ℎ
||| (2)
𝑓𝑤,𝑖(𝑃𝑤,𝑖) =Direct cost of wind power+reserve cost+penalty cost+probabilistic density cost
= ∑ [𝑔𝑤,𝑖(𝑃𝑤,𝑖)
𝑅𝐸𝑆
𝑖=1 + 𝐾𝑅𝑤,𝑖 ∫ (𝑃𝑤,𝑖 − 𝑃𝑤𝑟,𝑖)𝑓
𝑤𝑟(𝑃𝑤𝑟,𝑖)𝑑𝑃(𝑤𝑟, 𝑖)
𝑃𝑤,𝑖
0
+
𝐾𝑃𝑤,𝑖 ∫ (𝑃𝑤𝑟,𝑖 − 𝑃𝑤,𝑖)𝑓
𝑤𝑟(𝑃𝑤𝑟,𝑖)𝑑𝑃(𝑤𝑟, 𝑖)
𝑃𝑤𝑟,𝑖
𝑃𝑤,𝑖
] + (
𝐾
𝑐
) (
𝜐
𝑐
)
𝑘−1
𝑒
−(
𝜐
𝑐
)
𝑘
(𝑓𝑜𝑟0 ≤ 𝜐 ≤ ∞) (3)
( )=
i
so
i
so P
f ,
, Direct cost of solar power+reserve cost+penalty cost
= ∑ [𝑓𝑠𝑜,𝑗(𝑃𝑠𝑜,𝑗)
𝑅𝐸𝑆
𝑗=1 + 𝐾𝑅𝑠,𝑗𝑓
𝑠(𝑃𝑠,𝑗 < 𝑃𝑠𝑟,𝑗)(𝑃𝑠𝑟,𝑗 − 𝐸(𝑃𝑠,𝑗 > 𝑃𝑠𝑟,𝑗)) +
𝐾𝑃𝑠,𝑗𝑓
𝑠(𝑃𝑠,𝑗 > 𝑃𝑠𝑟,𝑗)(𝐸(𝑃𝑠,𝑗 > 𝑃𝑠𝑟,𝑗) − 𝑃𝑠𝑟,𝑗)] (4)
𝑓𝑡(𝑃𝑡) is the sum of electrical thermal generator sources cost and valve point effect cost. 𝑓𝑤,𝑖(𝑃𝑤,𝑖) and
𝑓𝑠𝑜,𝑗(𝑃𝑠𝑜,𝑗) is wind (w) and solar (so) based renewable energy ith
and jth
units cost characteristics, respectively.
2.2. Constraints
Power balance and power flow equations are represented by equality constraints. The power balance
equations of renewable and non-renewable energy sources with RES units are expressed as (5), (6):
𝑃𝑖𝑛𝑗𝑘,ℎ − ∑ 𝑉𝑘,ℎ
𝑁
𝑖=1 𝑉𝐿,ℎ[(𝐺𝑘𝑠 𝑐𝑜𝑠( 𝛿𝑙,ℎ − 𝛿𝑘,ℎ)) + (𝐵𝑘𝑙 𝑠𝑖𝑛( 𝛿𝑙,ℎ − 𝛿𝑘,ℎ))] = 0 (5)
𝑄𝑖𝑛𝑗𝑘,ℎ − ∑ 𝑉𝑘,ℎ
𝑁
𝑖=1 𝑉𝐿,ℎ[(𝐺𝑘𝑠 𝑠𝑖𝑛( 𝛿𝑙,ℎ − 𝛿𝑘,ℎ)) + (𝐵𝑘𝑙 𝑐𝑜𝑠( 𝛿𝑙,ℎ − 𝛿𝑘,ℎ))] = 0 (6)
NR represents No. of RES units with renewable energy sources. The load bus is restricted by functional
operational limitations incorporating voltage magnitude and the information regarding the reactive power
capabilities and limits the branch flow of the DG units are the inequality constraints and expressed as (7)-(9):
𝑉𝑖
𝑚𝑖𝑛
≤ 𝑉𝑖 ≤ 𝑉𝑖
𝑚𝑎𝑥
𝑖 = 1, … , 𝑁𝐿 (7)
𝑄𝑖
𝑚𝑖𝑛
≤ 𝑄𝑖 ≤ 𝑄𝑖
𝑚𝑎𝑥
𝑖 = 1, …, 𝑁𝑃𝑉 (8)
𝑆𝑖 ≤ 𝑆𝑖
𝑚𝑎𝑥
𝑖 = 1, … , 𝑁 (9)
Below constraints define the feasibility region problem of control variables. The variables may be
active power output limits of RES unit, root node voltage magnitude limits and such.

 ISSN: 2088-8708
4838
𝑃𝑖
𝑚𝑖𝑛
≤ 𝑃𝑖 ≤ 𝑃𝑖
𝑚𝑎𝑥
𝑖 = 1, … , 𝑁𝑁𝑅 (10)
𝑉0
𝑚𝑖𝑛
≤ 𝑉0 ≤ 𝑉0
𝑚𝑎𝑥
𝑖 (11)
𝑉𝑖
𝑚𝑖𝑛
≤ 𝑉𝑖 ≤ 𝑉𝑖
𝑚𝑎𝑥
𝑖 = 1, … , 𝑁𝑃𝑉 (12)
𝑡𝑖
𝑚𝑖𝑛
≤ 𝑡𝑖 ≤ 𝑡𝑖
𝑚𝑎𝑥
𝑖 = 1, … , 𝑁𝑇 (13)
𝑄𝐶𝑖
𝑚𝑖𝑛
≤ 𝑄𝐶𝑖 ≤ 𝑄𝐶𝑖
𝑚𝑎𝑥
𝑖 = 1, … , 𝑁𝐶 (14)
The magnitude of Load bus voltage along with the reactive power output of the RES unit and its branch
loading are included concerning theobjective function in the form of a quadratic penalty term [18]. These
constitute the Inequality constraints of the dependent variables.
3. MODELING OF RES UNITS FOR OPTIMAL POWER FLOW
3.1. Wind turbine
Wind turbine power output mainly dependent on wind turbine power curve and wind speed at a
certain locality. The output is at zero for wind speeds lying between the cut-off speed and the cut-in speed,
and equal to the rated power for speeds between the rated speed and the cut-off speed. The wind turbine
power curve can be mathematically designed by splitting the function into four different parts [19]–[22]:
𝑃𝑜𝑢𝑡 =
{
0, 𝑣 ≤ 𝑣𝑖𝑛
𝑣2−𝑣𝑖𝑛
2
𝑣𝑟
2−𝑣𝑖𝑛
2 ⋅ 𝑃
𝑤𝑟, 𝑣𝑖𝑛 < 𝑣 ≤ 𝑣𝑟
𝑃
𝑤𝑟, 𝑣𝑟 < 𝑣 ≤ 𝑣𝑜𝑢𝑡
0, 𝑣 > 𝑣𝑜𝑢𝑡
(15)
As a result, the Weibull PDF was utilized for wind speed estimation, and the international global factor (IGF)
for defining wind speed. As a result, (16) and (17) gives the Weibull PDF:
𝑓
𝑤(𝑃𝑤)|𝑃𝑤=0 = 𝐶𝑑𝑓(𝜐𝑖𝑛) + (1 − 𝐶𝑑𝑓(𝜐𝑜𝑢𝑡) = 1 − 𝑒𝑥𝑝( −
𝜐𝑖𝑛
𝐶
)𝑘
+ 𝑒𝑥𝑝( −
𝜐𝑜𝑢𝑡
𝐶
)𝑘
(16)
𝑓
𝑤(𝑃𝑤)|𝑃𝑤=𝑃𝑟
= 𝐶𝑑𝑓(𝜐𝑜𝑢𝑡) + (1 − 𝐶𝑑𝑓(𝜐𝑟) = 𝑒𝑥𝑝( −
𝜐𝑟
𝐶
)𝑘
− 𝑒𝑥𝑝( −
𝜐𝑜𝑢𝑡
𝐶
)𝑘
(17)
Overall generator cost.
𝐶𝑊𝐺 = ∑ [𝐶𝑤,𝑗(𝑃𝑤𝑠,𝑗) + 𝐶𝑅𝑤,𝑗(𝑃𝑤𝑠,𝑗 − 𝑃𝑤𝑎𝑣,𝑗) + 𝐶𝑃𝑤,𝑗(𝑃𝑤𝑎𝑣,𝑗 − 𝑃𝑤𝑠,𝑗)]
𝑁𝑤ℎ
𝑗=1 (18)
3.2. Photovoltaic cost
Solar irradiance and ambient temperature are detrimental factors to output power of PV module
along with the characteristics of the module itself [25]–[27]. The output power of the PV module Ppv (19) is
given by (19)-(22):
𝑃
𝑝𝑣 = 𝑃𝑆𝑇𝐶
𝐼𝑠
1000
[1 + 𝛾(𝑇𝑐 − 25)] (19)
𝐶𝑠,𝑘(𝑃𝑠𝑠,𝑘) = 𝐺𝑘𝑃𝑠𝑠,𝑘 (20)
𝐶𝑅𝑠,𝑘(𝑃𝑠𝑠,𝑘 − 𝑃𝑠𝑎𝑣,𝑘) = 𝐾𝑅𝑠,𝑘(𝑃𝑠𝑠,𝑘 − 𝑃𝑠𝑎𝑣,𝑘) = 𝐾𝑅𝑠,𝑘𝑓
𝑠(𝑃𝑠𝑎𝑣,𝑘 < 𝑃𝑠𝑠,𝑘)
(𝑃𝑠𝑠,𝑘 − 𝐸(𝑃𝑠𝑎𝑣,𝑘 < 𝑃𝑠𝑠,𝑘)) (21)
𝐶𝑃𝑠,𝑘(𝑃𝑠𝑎𝑣,𝑘 − 𝑃𝑠𝑠,𝑘) = 𝐾𝑃𝑠,𝑘(𝑃𝑠𝑎𝑣,𝑘 − 𝑃𝑠𝑠,𝑘) = 𝐾𝑃𝑠,𝑘𝑓
𝑠(𝑃𝑠𝑎𝑣,𝑘 > 𝑃𝑠𝑠,𝑘)
(𝐸(𝑃𝑠𝑎𝑣,𝑘 > 𝑃𝑠𝑠,𝑘) − 𝑃𝑠𝑠,𝑘) (22)
Log normal PDF at irradiance (Gs): at any one time, the future system load requirement is unknown. Normal
and uniform PDFs are the two most often utilized PDFs for predicting load demand uncertainty. Normal PDF

4839
is utilized to represent the load distribution in this work. The normal distribution’s PDF for an undetermined
load ‘l’ is given by (23),
𝑓𝐺(𝐺𝑠) =
1
𝐺𝑠𝜎√2𝜋
𝑒𝑥𝑝 (
−(𝑙𝑎𝑥−𝜇)2
2𝜎2 ) for Gs>0 (23)
here μL and σL are the mean and standard deviation of the uncertain load.
𝐶𝑆𝐺 = ∑ (𝐶𝑠,𝑘(𝑃𝑠𝑠,𝑘) + 𝐶𝑅𝑠,𝑘(𝑃𝑠𝑠,𝑘 − 𝑃𝑠𝑎𝑣,𝑘) + 𝐶𝑃𝑠,𝑘(𝑃𝑠𝑎𝑣,𝑘 − 𝑃𝑠𝑠,𝑘))
𝑁𝑆𝐺
𝑘=1 (24)
4. WHALE OPTIMIZATION ALGORITHM
The methodology proposed in this paper for identifying the optimum size for OPF solution is
obtained by using WOA. It is a meta-heuristic algorithm first introduced by Seyedali Mirjalili and Andrew
Lewis in 2016. This algorithm emulates the communal hunting behavior of Humpback whales. The special
hunting method of humpback whales called the bubble-net attacking method which includes encircling the
prey, spiraling update position, and searching for the prey is utilized. The algorithm performs the exploitation
phase based on the first two approaches and the exploration phase based on the last approach.
− Searching the prey
Position of whale is modified by employing,
𝐻
→
= |𝐷
→
. 𝑍
→
𝑟𝑎𝑛𝑑 − 𝑍
→
| (25)
𝑍
→
(𝑖𝑡𝑒𝑟 + 1) = 𝑍
→
𝑟𝑎𝑛𝑑 − 𝐵
→
. 𝐻
→
(26)
𝐵
⃗ = 2. 𝑎. 𝑟1
⃗⃗⃗ − 𝑎 (27)
𝐷 =
⃗⃗⃗⃗⃗⃗⃗⃗ 2. 𝑟2 (28)
a ɛ [2, 0], r1 and r2 ɛ [0, 1]
− Encircling prey
In this stage whale identifies its prey with the below:
𝐻
→
= |𝐷
→
× 𝑍𝑝
→
(𝑖𝑡𝑒𝑟) − 𝑍(𝑖𝑡𝑒𝑟)
→
| (29)
𝑍
→
(𝑖𝑡𝑒𝑟 + 1) = 𝑍𝑝
→
(𝑖𝑡𝑒𝑟) − 𝐵
→
× 𝐻
→
(30)
− Bubble-net aggressive method:
𝑍
→
(𝑖𝑡𝑒𝑟 + 1) = 𝐻
→
𝑒𝑏𝑙
. 𝑐𝑜𝑠(2𝜋𝑙) + 𝑍
→
(𝑖𝑡𝑒𝑟) (31)
𝐻
→
= |𝑍
→
𝑝(𝑖𝑡𝑒𝑟) − 𝑍
→
(𝑖𝑡𝑒𝑟)| (32)
The measured model for this is given as (33):
( )
( )
( ) ( )
. 0.5
1
. cos 2 0.5
bl
p
Z iter B Hifp
Z iter
H e l Z iter ifp

→ →
→
→

− 


+ = 

+ 

 (33)
5. RESULT AND ANALYSIS
In this result analysis, the proposed WOA results are distinguished from other promising methods to
show the effectiveness of the work. In this section, results are compared with NSGA-II, GWO, and hybrid

 ISSN: 2088-8708
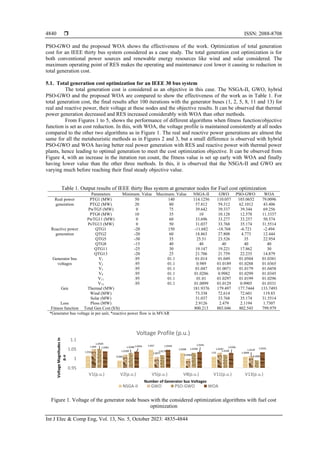
4840
PSO-GWO and the proposed WOA shows the effectiveness of the work. Optimization of total generation
cost for an IEEE thirty bus system considered as a case study. The total generation cost optimization is for
both conventional power sources and renewable energy resources like wind and solar considered. The
maximum operating point of RES makes the operating and maintenance cost lower it causing to reduction in
total generation cost.
5.1. Total generation cost optimization for an IEEE 30 bus system
The total generation cost is considered as an objective in this case. The NSGA-II, GWO, hybrid
PSO-GWO and the proposed WOA are compared to show the effectiveness of the work as in Table 1. For
total generation cost, the final results after 100 iterations with the generator buses (1, 2, 5, 8, 11 and 13) for
real and reactive power, their voltage at these nodes and the objective results. It can be observed that thermal
power generation decreased and RES increased considerably with WOA than other methods.
From Figures 1 to 5, shows the performance of different algorithms when fitness function/objective
function is set as cost reduction. In this, with WOA, the voltage profile is maintained consistently at all nodes
compared to the other two algorithms as in Figure 1. The real and reactive power generations are almost the
same for all the metaheuristic methods as in Figures 2 and 3, but a small difference is observed with hybrid
PSO-GWO and WOA having better real power generation with RES and reactive power with thermal power
plants, hence leading to optimal generation to meet the cost optimization objective. It can be observed from
Figure 4, with an increase in the iteration run count, the fitness value is set up early with WOA and finally
having lower value than the other three methods. In this, it is observed that the NSGA-II and GWO are
varying much before reaching their final steady objective value.
Table 1. Output results of IEEE thirty Bus system at generator nodes for Fuel cost optimization
Parameters Minimum. Value Maximum. Value NSGA-II GWO PSO-GWO WOA
Real power
generation
PTG1 (MW) 50 140 114.1256 110.057 103.0652 79.0096
PTG2 (MW) 20 80 57.812 59.312 62.1012 43.406
PwTG5 (MW) 0 75 39.642 39.337 39.344 69.256
PTG8 (MW) 10 35 10 10.128 12.578 11.3337
PwTG11 (MW) 0 60 33.696 33.277 33.257 50.574
PsTG13 (MW) 0 50 31.037 33.768 35.174 31.5514
Reactive power
generation
QTG1 -20 150 -11.682 -18.768 -6.721 -2.494
QTG2 -20 60 18.863 27.808 4.773 12.444
QTG5 -30 35 25.51 23.526 35 22.954
QTG8 -15 40 40 40 40 40
QTG11 -25 30 19.147 19.221 17.862 30
QTG13 -20 25 21.706 21.759 22.235 14.879
Generator bus
voltages
V1 .95 01.1 01.014 01.049 01.0504 01.0381
V2 .95 01.1 0.989 01.0189 01.0288 01.0365
V5 .95 01.1 01.047 01.0071 01.0179 01.0458
V8 .95 01.1 01.0286 0.9982 01.0299 01.0345
V11 .95 01.1 01.01 01.0297 01.0199 01.0296
V13 .95 01.1 01.0099 01.0129 0.9905 01.0331
Gen Thermal (MW) 181.9376 179.497 177.7444 133.7493
Wind (MW) 73.338 72.614 72.601 119.83
Solar (MW) 31.037 33.768 35.174 31.5514
Loss Ploss (MW) 2.9126 2.479 2.1194 1.7307
Fitness function Total Gen Cost ($/h) 800.213 803.046 802.545 799.979
*Generator bus voltage in per unit, *reactive power flow is in MVAR
Figure 1. Voltage of the generator node buses with the considered optimization algorithms with fuel cost
optimization
1.014
0.989
1.047
1.0286
1.01 1.0099
1.049
1.0189
1.0071
0.9982
1.0297 1.0129
1.0504
1.0288
1.0179
1.0299
1.0199
0.9905
1.0381 1.0365 1.0458 1.0345
1.0296 1.0331
0.95
1
1.05
1.1
V1(p.u.) V2(p.u.) V5(p.u.) V8(p.u.) V11(p.u.) V13(p.u.)
Voltage
Magnitudes
in
p.u
Number of Generator bus Voltages
Voltage Profile (p.u.)
NSGA-II GWO PSO-GWO WOA

4841
Figure 2. Real power generation at node buses for fuel cost optimization
Figure 3. Reactive power generation at node buses for fuel cost optimization
The fitness curve of total generation cost optimization as objective using WOA algorithm is shown
in Figure 5 for 100 iterations. The objective function with WOA started at 819 $/hr in the1st iteration,
reached 804, 802, and almost 800 in the next 10, 20 and 30 iterations. The value at 100 iteration is almost
equal to the value at 50 iterations as the system is running towards convergence.
Figure 4. Objective functions during the iterations run under fuel cost optimization
114.1256
57.812
39.642
10
33.696 31.037
110.057
59.312
39.337
10.128
33.277 33.768
103.0652
62.1012
39.344
12.578
33.257 35.174
79.0096
43.406 69.256
11.3337
50.574
31.5514
0
50
100
150
PG1(MW) PG2(MW) PG5(MW) PG8(MW) PG11(MW) PG13(MW)
Real
Power
Generation
in
MW
Number of Real Power Generators
Generators Real Power
-11.682
18.863
25.51
40
19.147
21.706
-18.768
27.808
23.526
40
19.221
21.759
-6.721
4.773
35
40
17.862
22.235
-2.494
12.444
22.954
40
30
14.879
-40
-20
0
20
40
60
QG1(MW) QG2(MW) QG5(MW) QG8(MW) QG11(MW) QG13(MW)
Reactive
Power
Generation
in
MVAr
Number of Reactive Power Generators
Reactive Power (MVAr)
PSO GWO PSO-GWO WOA
823.213
810.213
803.626
800.213 800.213
824.207
809.566
806.607
803.047 803.046
822.736
807.022
805.501
802.546 802.545
819.979
804.601
802.47
799.978
799.977
780
790
800
810
820
830
Run 1 Run 10 Run 30 Run 50 Run 100
Fitness
Function
value
Number of Runs
Fitness Curve with iterations

 ISSN: 2088-8708
4842
Figure 5. Optimal cost fitness curve for Fuel cost optimization with a different algorithm for an IEEE thirty
bus system
6. CONCLUSION
This paper proposed a novel WOA incorporating issue of MOOPF-WS. It has taken into account
several energy sources including distributed energy resources into the grid. Also, various PDFs were utilized
for representing uncertainty in RES and load demand. In order to define non-dominated ranks and also the
solutions’ densities, the WOA used rapid non-dominated sorting approach methodology and the crowding
distance methodology. WOA was successfully deployed on the modified 30-bus system with RES.
Furthermore, the WOA performance was compared to that of the NSGA-II, GWO and PSO-GWO. In all
situations, the WOA outperformed the other three approaches in terms of convergence. Furthermore, when
compared to major studies in the literature, WOA obtained higher-quality solutions in all similar
circumstances. These demonstrated the WOA’s capabilities and proved its capability in dealing with the
MOOPF-WS challenge.WOA can also help in maintaining a better voltage profile, reduce real and reactive
power flow losses, and minimize generation costs by optimally using RES as compared to other algorithms.
REFERENCES
[1] W.-M. Lin and S.-J. Chen, “Bid-based dynamic economic dispatch with an efficient interior point algorithm,” International
Journal of Electrical Power and Energy Systems, vol. 24, no. 1, pp. 51–57, Jan. 2002,
doi: 10.1016/S0142-0615(01)00007-2.
[2] K. Widarsono, F. D. Murdianto, M. Nur, and A. Mustofa, “Optimal power flow using particle swarm optimization for IEEE 30
bus,” Journal of Physics: Conference Series, vol. 1595, no. 1, Jul. 2020, doi: 10.1088/1742-6596/1595/1/012033.
[3] K. Karchung, “Optimization techniques to enhance voltage stability in power system: a review towards improving bhutanese
power network,” International Journal of Engineering and Applied Sciences (IJEAS), vol. 5, no. 1, pp. 17–29, 2022.
[4] M. H. Nadimi-Shahraki, S. Taghian, S. Mirjalili, L. Abualigah, M. Abd Elaziz, and D. Oliva, “EWOA-OPF: effective whale
optimization algorithm to solve optimal power flow problem,” Electronics, vol. 10, no. 23, Nov. 2021, doi:
10.3390/electronics10232975.
[5] C. Shilaja and T. Arunprasath, “Optimal power flow using moth swarm algorithm with gravitational search algorithm considering
wind power,” Future Generation Computer Systems, vol. 98, pp. 708–715, Sep. 2019, doi: 10.1016/j.future.2018.12.046.
[6] M. Sukumar and M. Suneethaa, “Combined economic emission and economic dispatch for optimal power flow using glow worm
swarm optimization algorithm,” International Journal of Advanced Technology and Innovative Research, vol. 6, pp. 1188–1192,
2014.
[7] H. Buch, I. N. Trivedi, and P. Jangir, “Moth flame optimization to solve optimal power flow with non-parametric statistical
evaluation validation,” Cogent Engineering, vol. 4, no. 1, Jan. 2017, doi: 10.1080/23311916.2017.1286731.
[8] A. R. Bhowmik and A. K. Chakraborty, “Solution of optimal power flow using non dominated sorting multi objective opposition
based gravitational search algorithm,” International Journal of Electrical Power and Energy Systems, vol. 64, pp. 1237–1250,
Jan. 2015, doi: 10.1016/j.ijepes.2014.09.015.
[9] S. Abd el-sattar, S. Kamel, M. Ebeed, and F. Jurado, “An improved version of salp swarm algorithm for solving optimal power
flow problem,” Soft Computing, vol. 25, no. 5, pp. 4027–4052, Mar. 2021, doi: 10.1007/s00500-020-05431-4.
[10] S. A. El-Sattar, S. Kamel, R. A. El Sehiemy, F. Jurado, and J. Yu, “Single- and multi-objective optimal power flow frameworks
using Jaya optimization technique,” Neural Computing and Applications, vol. 31, no. 12, pp. 8787–8806, Dec. 2019, doi:
10.1007/s00521-019-04194-w.
[11] T. Samakpong, W. Ongsakul, and M. N. Madhu, “Optimal power flow considering cost of wind and solar power uncertainty using
particle swarm optimization,” in Advances in Intelligent Systems and Computing, Springer International Publishing, 2020,
pp. 190–203.
[12] N. Karthik, A. K. Parvathy, R. Arul, and K. Padmanathan, “Multi-objective optimal power flow using a new heuristic
optimization algorithm with the incorporation of renewable energy sources,” International Journal of Energy and Environmental
Engineering, vol. 12, no. 4, pp. 641–678, Dec. 2021, doi: 10.1007/s40095-021-00397-x.
795
805
815
825
835
1
5
9
13
17
21
25
29
33
37
41
45
49
53
57
61
65
69
73
77
81
85
89
93
97
Fitness
Function
Value
Number of Iterations
Fitness Curve
NSGA-II GWO
PSO-GWO WOA

4843
[13] R. A. Swief, N. M. Hassan, H. M. Hasanien, A. Y. Abdelaziz, and M. Z. Kamh, “AC and DC optimal power flow incorporating
centralized/decentralized multi-region grid control employing the whale algorithm,” Ain Shams Engineering Journal, vol. 12, no.
2, pp. 1907–1922, Jun. 2021, doi: 10.1016/j.asej.2021.01.004.
[14] M. H. Nadimi-Shahraki, A. Fatahi, H. Zamani, S. Mirjalili, and D. Oliva, “Hybridizing of whale and moth-flame optimization
algorithms to solve diverse scales of optimal power flow problem,” Electronics, vol. 11, no. 5, Mar. 2022, doi:
10.3390/electronics11050831.
[15] D. Prasad, A. Mukherjee, G. Shankar, and V. Mukherjee, “Application of chaotic whale optimisation algorithm for transient
stability constrained optimal power flow,” IET Science, Measurement and Technology, vol. 11, no. 8, pp. 1002–1013, Nov. 2017,
doi: 10.1049/iet-smt.2017.0015.
[16] T. H. B. Huy, T. P. Nguyen, N. Mohd Nor, I. Elamvazuthi, T. Ibrahim, and D. N. Vo, “Performance improvement of
multiobjective optimal power flow-based renewable energy sources using intelligent algorithm,” IEEE Access, vol. 10, pp.
48379–48404, 2022, doi: 10.1109/ACCESS.2022.3170547.
[17] L. Shi, C. Wang, L. Yao, Y. Ni, and M. Bazargan, “Optimal power flow solution incorporating wind power,” IEEE Systems
Journal, vol. 6, no. 2, pp. 233–241, Jun. 2012, doi: 10.1109/JSYST.2011.2162896.
[18] R. Roy and H. T. Jadhav, “Optimal power flow solution of power system incorporating stochastic wind power using Gbest guided
artificial bee colony algorithm,” International Journal of Electrical Power and Energy Systems, vol. 64, pp. 562–578, Jan. 2015,
doi: 10.1016/j.ijepes.2014.07.010.
[19] Z. Q. Xie, T. Y. Ji, M. S. Li, and Q. H. Wu, “Quasi-Monte Carlo based probabilistic optimal power flow considering the
correlation of wind speeds using copula function,” IEEE Transactions on Power Systems, vol. 33, no. 2, pp. 2239–2247, Mar.
2018, doi: 10.1109/TPWRS.2017.2737580.
[20] P. P. Biswas, P. N. Suganthan, and G. A. J. Amaratunga, “Optimal power flow solutions incorporating stochastic wind and solar
power,” Energy Conversion and Management, vol. 148, pp. 1194–1207, Sep. 2017, doi: 10.1016/j.enconman.2017.06.071.
[21] S. Pandya and H. R. Jariwala, “Single- and multiobjective optimal power flow with stochastic wind and solar power plants using
moth flame optimization algorithm,” Smart Science, vol. 10, no. 2, pp. 77–117, Apr. 2022,
doi: 10.1080/23080477.2021.1964692.
[22] T. Samakpong, W. Ongsakul, and N. M. Manjiparambil, “Optimal power flow incorporating renewable uncertainty related
opportunity costs,” Computational Intelligence, vol. 38, no. 3, pp. 1057–1082, Jun. 2022, doi: 10.1111/coin.12316.
[23] Z. Ullah, S. Wang, J. Radosavljevic, and J. Lai, “A solution to the optimal power flow problem considering WT and PV
generation,” IEEE Access, vol. 7, pp. 46763–46772, 2019, doi: 10.1109/ACCESS.2019.2909561.
[24] S. Shargh, B. K. Ghazani, B. Mohammadi-ivatloo, H. Seyedi, and M. Abapour, “Probabilistic multi-objective optimal power flow
considering correlated wind power and load uncertainties,” Renewable Energy, vol. 94, pp. 10–21, Aug. 2016, doi:
10.1016/j.renene.2016.02.064.
[25] K. Pandiarajan and C. K. Babulal, “Fuzzy harmony search algorithm based optimal power flow for power system security
enhancement,” International Journal of Electrical Power and Energy Systems, vol. 78, pp. 72–79, Jun. 2016, doi:
10.1016/j.ijepes.2015.11.053.
[26] X. Lu et al., “A real-time alternating direction method of multipliers algorithm for nonconvex optimal power flow problem,”
IEEE Transactions on Industry Applications, vol. 57, no. 1, pp. 70–82, Jan. 2021, doi: 10.1109/TIA.2020.3029549.
[27] M. Riaz, A. Hanif, S. J. Hussain, M. I. Memon, M. U. Ali, and A. Zafar, “An optimization-based strategy for solving optimal
power flow problems in a power system integrated with stochastic solar and wind power energy,” Applied Sciences, vol. 11, no.
15, Jul. 2021, doi: 10.3390/app11156883.
[28] M. Aien, M. Fotuhi-Firuzabad, and M. Rashidinejad, “Probabilistic optimal power flow in correlated hybrid
wind–photovoltaic power systems,” IEEE Transactions on Smart Grid, vol. 5, no. 1, pp. 130–138, Jan. 2014, doi:
10.1109/TSG.2013.2293352.
[29] E. DallAnese, K. Baker, and T. Summers, “Chance-constrained AC optimal power flow for distribution systems with
renewables,” IEEE Transactions on Power Systems, vol. 32, no. 5, pp. 3427–3438, 2017,
doi: 10.1109/TPWRS.2017.2656080.
[30] B. V. Rao and G. V. N. Kumar, “Optimal power flow by BAT search algorithm for generation reallocation with unified power
flow controller,” International Journal of Electrical Power and Energy Systems, vol. 68, pp. 81–88, Jun. 2015, doi:
10.1016/j.ijepes.2014.12.057.
[31] A. E. Chaib, H. R. E. H. Bouchekara, R. Mehasni, and M. A. Abido, “Optimal power flow with emission and non-smooth cost
functions using backtracking search optimization algorithm,” International Journal of Electrical Power and Energy Systems, vol.
81, pp. 64–77, Oct. 2016, doi: 10.1016/j.ijepes.2016.02.004.
[32] S. S. Reddy and P. R. Bijwe, “Efficiency improvements in meta-heuristic algorithms to solve the optimal power flow problem,”
International Journal of Electrical Power and Energy Systems, vol. 82, pp. 288–302, 2016,
doi: 10.1016/j.ijepes.2016.03.028.
[33] D. K. Molzahn et al., “A survey of distributed optimization and control algorithms for electric power systems,” IEEE
Transactions on Smart Grid, vol. 8, no. 6, pp. 2941–2962, Nov. 2017, doi: 10.1109/TSG.2017.2720471.
BIOGRAPHIES OF AUTHORS
TentuPapi Naidu received his Bachelor of Engineering degree in Electrical and
Electronics Engineering in 2008. He received his Master of Engineering degree in Power and
Industrial drives in 2014 from JNTU Kakinada, A.P, India. He is presently pursuing his Ph.D.
degree in Electrical Engineering from Annamalai University, Annamalainagar, Tamilnadu. He
is an Associate Professor in the Electrical and Electronics Engineering Department at Lendi
Institute of Engineering and Technology, Vijayanagaram, AP. His research interests are in
Power Systems and Power Electronics. He can be contacted at email: tpneee@gmail.com.

 ISSN: 2088-8708
4844
Ganapathy Balasubramanian received his Bachelor of Engineering degree in
Electrical and Electronics Engineering in 2000. He received his Master of Engineering degree
in Power System Engineering in 2005 from Annamalai University, Annamalainagar,
Tamilnadu, India. He received his Ph.D. degree in Electrical Engineering from Annamalai
University, Annamalainagar, Tamilnadu, India in 2014. He is Associate Professor in the
Electrical Engineering Department at Government College of Engineering, Tirunelveli,
Tamilnadu, India. His research interests are in electrical machines, power systems, power
electronics, solar, wind energy and microgrid applications. He can be contacted at email:
balaraje05@gmail.com.
Bathina Venkateswara Rao received his Bachelor degree in Electrical and
Electronics Engineering from College of Engineering, Gandhi Institute of Technology and
Management (GITAM), Visakhapatnam, India in 2000, and the Master degree in Electrical
Power Engineering from the College of Engineering, JNTU, Hyderabad in 2007 and received
Ph.D. from Jawaharlal Nehru Technological University, Hyderabad in 2015. He is presently
working as an Associate Professor in the Department of Electrical and Electronics
Engineering, V R Siddhartha Engineering College, Vijayawada. His research interests are
power system stability analysis, FACTS devices, and power system optimization. He has
published several research papers in national and international conferences and journals. He
can be contacted at email: drbvrao@vrsiddhartha.ac.in, ResearcherID: J-1715-2019,
SciProfiles: 2454649

Optimal power flow with distributed energy sources using whale optimization algorithm

Recommended

More Related Content

Similar to Optimal power flow with distributed energy sources using whale optimization algorithm (20)

More from IJECEIAES (20)

Recently uploaded (20)

Optimal power flow with distributed energy sources using whale optimization algorithm