Parallel_Algorithms_In_Combinatorial_Optimization_Problems.ppt

CS 6260
PARALLEL COMPUTATION
PARALLEL ALGORITHMS IN COMBINATORIAL
OPTIMIZATION PROBLEMS
Professor:
Elise De Doncker
Presented By:
Lina Hussein
1

TOPICS COVERED ARE:
 Backtracking
 Branch and bound
 Divide and conquer
 Greedy Methods
 Short paths algorithms
2

BRANCH AND BOUND
 Branch and bound (BB) is a general algorithm for
finding optimal solutions of various optimization
problems, especially in discrete and combinatorial
optimization. It consists of a systematic enumeration of
all candidate solutions, where large subsets of fruitless
candidates are discarded en masse (all together), by
using upper and lower estimated bounds of the quantity
being optimized.
3

BRANCH AND BOUND
 If we picture the subproblems graphically, then we form a
search tree.
 Each subproblem is linked to its parent and eventually to its
children.
 Eliminating a problem from further consideration is called
pruning or fathoming.
 The act of bounding and then branching is called
processing.
 A subproblem that has not yet been considered is called a
candidate for processing.
 The set of candidates for processing is called the candidate
list.
 Going back on the path from a node to its root is called
backtracking.
4

BACKTRACKING
 Backtracking is a general algorithm for finding all (or
some) solutions to some computational problem, that
incrementally builds candidates to the solutions, and
abandons each partial candidate ("backtracks") as soon
as it determines that it cannot possibly be completed to a
valid solution..
 The Algorithm systematically searches for a solution to a
problem among all available options. It does so by
assuming that the solutions are represented by vectors
(v1, ..., vi) of values and by traversing in a depth first
manner the domains of the vectors until the solutions are
found. 5

BACKTRACKING
 A systematic way to iterate through all the possible
configurations of a search space.
 Solution: a vector v = (v1,v2,…,vi)
 At each step, we start from a given partial solution,
say, v=(v1,v2,…,vk), and try to extend it by adding
another element at the end.
 If so, we should count (or print,…) it.
 If not, check whether possible extension exits.
 If so, recur and continue
 If not, delete vk and try another possibility.
ALGORITHM try(v1,...,vi)
IF (v1,...,vi) is a solution THEN RETURN (v1,...,vi)
FOR each v DO
IF (v1,...,vi,v) is acceptable vector THEN sol = try(v1,...,vi,v)
IF sol != () THEN RETURN sol
END
END
RETURN () 6

PRUNING SEARCH
 If Si is the domain of vi, then S1 × ... × Sm is the
solution space of the problem. The validity criteria
used in checking for acceptable vectors determines
what portion of that space needs to be searched, and
so it also determines the resources required by the
algorithm.
 To make a backtracking program efficient enough to
solve interesting problems, we must prune the search
space by terminating for every search path the instant
that is clear not to lead to a solution.
7
S1
S2 S2
V1
.
.
.
V2
.
.
...........................................................

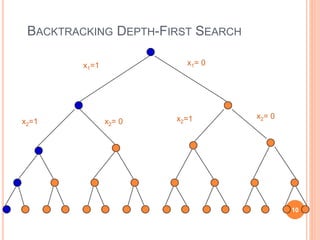
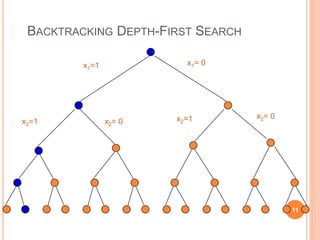
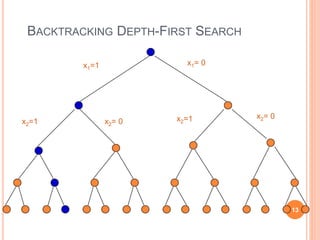
BACKTRACKING
 The traversal of the solution space can be represented by
a depth-first traversal of a tree. The tree itself is rarely
entirely stored by the algorithm in discourse; instead just
a path toward a root is stored, to enable the backtracking.
 When you move forward on an x =1 branch, add to a
variable that keeps track of the sum of the subset
represented by the node. When you move back on an x =
1 branch, subtract. Moving in either direction along an x =
0 branch requires no add/subtract. When you reach a
node with the desired sum, terminate. When you reach a
node whose sum exceeds the desired sum, backtrack; do
not move into this nodes subtrees. When you make a
right child move see if the desired sum is attainable by
adding in all remaining integers; for this keep another
variable that gives you the sum of the remaining integers.
8

BACKTRACKING DEPTH-FIRST SEARCH
x1=1 x1= 0
x2=1 x2= 0 x2=1 x2= 0
9

x1=1 x1= 0
x2=1 x2= 0 x2=1 x2= 0
10

x1=1 x1= 0
x2=1 x2= 0 x2=1 x2= 0
11

x1=1 x1= 0
x2=1 x2= 0 x2=1 x2= 0
12

x1=1 x1= 0
x2=1 x2= 0 x2=1 x2= 0
13

x1=1 x1= 0
x2=1 x2= 0 x2=1 x2= 0
14

EXAMPLE
 Example of the use Branch and Bound & backtracking is
Puzzles!
 For such problems, solutions are at different levels of the
tree
http://www.hbmeyer.de/backtrack/backtren.htm
15
1 2 3 4
5 6 7 8
9 1011 12
131415
1
3
2
4
5
6
13
14
15
12
11 10
9 7
8

TOPICS COVERED ARE:
 Branch and bound
 Backtracking
 Divide and conquer
 Greedy Methods
16

DIVIDE AND CONQUER
 divide and conquer (D&C) is an important algorithm
design paradigm based on multi-branched recursion. The
algorithm works by recursively breaking down a problem
into two or more sub-problems of the same (or related)
type, until these become simple enough to be solved
directly. The solutions to the sub-problems are then
combined to give a solution to the original problem.
 This technique is the basis of efficient algorithms for all
kinds of problems, such as sorting (e.g., quick sort,
merge sort).
17

ADVANTAGES
 Solving difficult problems:
 Divide and conquer is a powerful tool for solving conceptually
difficult problems, such as the classic Tower of Hanoi puzzle: it
break the problem into sub-problems, then solve the trivial
cases and combine sub-problems to the original problem.
 Roundoff control
 In computations with rounded arithmetic, e.g. with floating
point numbers, a D&C algorithm may yield more accurate
results than any equivalent iterative method.
 Example, one can add N numbers either by a simple loop that
adds each datum to a single variable, or by a D&C algorithm
that breaks the data set into two halves, recursively computes
the sum of each half, and then adds the two sums. While the
second method performs the same number of additions as the
first, and pays the overhead of the recursive calls, it is usually
more accurate.
18

IN PARALLELISM...
 Divide and conquer algorithms are naturally
adapted for execution in multi-processor machines,
especially shared-memory systems where the
communication of data between processors does
not need to be planned in advance, because
distinct sub-problems can be executed on different
processors.
19

TOPICS COVERED ARE:
 Backtracking
 Divide and conquer
 Greedy Methods
20

GREEDY METHODS
A greedy algorithm:
 is any algorithm that follows the problem solving metaheuristic
of making the locally optimal choice at each stage with the hope
of finding the global optimum.
A metaheuristic method:
 Is method for solving a very general class of computational
problems that aims on obtaining a more efficient or more robust
procedure for the problem.
 Generally it is applied to problems for which there is no
satisfactory problem-specific algorithm designed to solve it.
 It targeted to the combinatorial optimization (problems that’s
are a problems in which has an optimization function to(
minimize or maximize) subject to some constraints and its goal
is to find the best possible solution
21

EXAMPLES
 The vehicle routing problem (VRP)
 A number of goods need to be moved from certain
pickup locations to other delivery locations. The goal is
to find optimal routes for a fleet of vehicles to visit the
pickup and drop-off locations.
 Travelling salesman problem
 Given a list of cities and their pair wise distances, the
task is to find a shortest possible tour that visits each
city exactly once.
 Coin Change
 (making change for n $ using minimum number of coins)
 The knapsack problem
 The Shortest Path Problem 22

KNAPSACK
 The knapsack problem or rucksack problem is a
problem in combinatorial optimization. It derives its
name from the following maximization problem of
the best choice of essentials that can fit into one
bag to be carried on a trip. Given a set of items,
each with a weight and a value, determine the
number of each item to include in a collection so
that the total weight is less than a given limit and
the total value is as large as possible.
23

THE ORIGINAL KNAPSACK PROBLEM (1)
 Problem Definition
 Want to carry essential items in one bag
 Given a set of items, each has
 A cost (i.e., 12kg)
 A value (i.e., 4$)
 Goal
 To determine the # of each item to include in a collection
so that
 The total cost is less than some given cost
 And the total value is as large as possible
24

THE ORIGINAL KNAPSACK PROBLEM (2)
 Three Types
 0/1 Knapsack Problem
 restricts the number of each kind of item to zero or one
 Bounded Knapsack Problem
 restricts the number of each item to a specific value
 Unbounded Knapsack Problem
 places no bounds on the number of each item
 Complexity Analysis
 The general knapsack problem is known to be NP-hard
 No polynomial-time algorithm is known for this problem
 Here, we use greedy heuristics which cannot guarantee the
optimal solution
25

0/1 KNAPSACK PROBLEM (1)
 Problem: John wishes to take n items on a trip
 The weight of item i is wi & items are all different (0/1 Knapsack Problem)
 The items are to be carried in a knapsack whose weight capacity is c
 When sum of item weights ≤ c, all n items can be carried in the
knapsack
 When sum of item weights > c, some items must be left behind
 Which items should be taken/left?
26

0/1 KNAPSACK PROBLEM (2)
 John assigns a profit pi to item i
 All weights and profits are positive numbers
 John wants to select a subset of the n items to take
 The weight of the subset should not exceed the capacity of the
knapsack (constraint)
 Cannot select a fraction of an item (constraint)
 The profit of the subset is the sum of the profits of the selected items
(optimization function)
 The profit of the selected subset should be maximum (optimization
criterion)
 Let xi = 1 when item i is selected and xi = 0 when item i is not selected
 Because this is a 0/1 Knapsack Problem, you can choose the item or
not choose it.
27

GREEDY ATTEMPTS FOR 0/1 KNAPSACK
 Apply greedy method:
 Greedy attempt on capacity utilization
 Greedy criterion: select items in increasing order of weight
 When n = 2, c = 7, w = [3, 6], p = [2, 10],
if only item 1 is selected  profit of selection is 2  not best
selection!
 Greedy attempt on profit earned
 Greedy criterion: select items in decreasing order of profit
 When n = 3, c = 7, w = [7, 3, 2], p = [10, 8, 6],
if only item 1 is selected  profit of selection is 10  not best
selection!
28

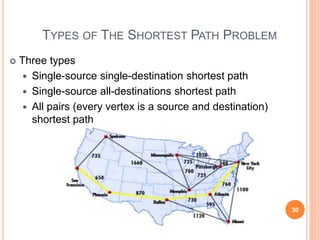
THE SHORTEST PATH PROBLEM
 Path length is sum of weights of edges on path in directed weighted
graph
 The vertex at which the path begins is the source vertex
 The vertex at which the path ends is the destination vertex
 Goal
 To find a path between two vertices such that the sum of the
weights of its edges is minimized
29

TYPES OF THE SHORTEST PATH PROBLEM
 Three types
 Single-source single-destination shortest path
 Single-source all-destinations shortest path
 All pairs (every vertex is a source and destination)
shortest path
30

SINGLE-SOURCE SINGLE-DESTINATION SHORTED
PATH
 Possible greedy algorithm
 Leave the source vertex using the cheapest edge
 Leave the current vertex using the cheapest edge to the next vertex
 Continue until destination is reached
 Try Shortest 1 to 7 Path by this Greedy Algorithm
 the algorithm does not guarantee the optimal solution
31
1
2
3
4
5
6
7
2
6
16
7
8
10
3
14
4
4
5 3
1

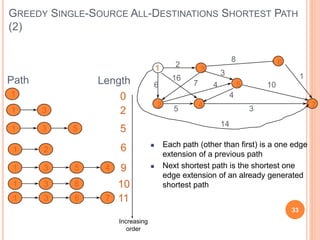
GREEDY SINGLE-SOURCE ALL-DESTINATIONS SHORTEST PATH
(1)
 Problem: Generating the shortest paths in increasing order of length from one
source to multiple destinations
 Greedy Solution
 Given n vertices, First shortest path is from the source vertex to itself
 The length of this path is 0
 Generate up to n paths (including path from source to itself) by the greedy
criteria
 from the vertices to which a shortest path has not been generated, select
one that results in the least path length
 Construct up to n paths in order of increasing length
Note:
The solution to the problem consists of up to n paths.
The greedy method suggests building these n paths in order of increasing length.
First build the shortest of the up to n paths (I.e., the path to the nearest destination).
Then build the second shortest path, and so on.
32

GREEDY SINGLE-SOURCE ALL-DESTINATIONS SHORTEST PATH
(2)
33
1
2
3
4
5
6
7
2
6
16
7
8
10
3
14
4
4
5 3
1
Path Length
1 0
1 3 2
1 3 5
5
1 2 6
1 3 9
5 4
1 3 10
6
1 3 11
6 7
 Each path (other than first) is a one edge
extension of a previous path
 Next shortest path is the shortest one
edge extension of an already generated
shortest path
Increasing
order

GREEDY SINGLE SOURCE ALL DESTINATIONS: EXAMPLE (1)
1
2
3
4
5
6
7
2
6
16
7
8
10
3
14
4
4
5 3
1
[1] [2] [3] [4] [5] [6] [7]
d
p
0
-
1
2
3
4 7
6
1
2
1
16
1
-
-
-
-
14
1
2
34

GREEDY SINGLE SOURCE ALL DESTINATIONS : EXAMPLE
(2)
1
2
3
4
5
6
7
2
6
16
7
8
10
3
14
4
4
5 3
1
[1] [2] [3] [4] [5] [6] [7]
d
p
1
0
-
6
1
2
1
16
1
-
-
-
-
14
1
1 3
2
5
6
5
3
10
3
5
35

(3)
1
2
3
4
5
6
7
2
6
16
7
8
10
3
14
4
4
5 3
1
[1] [2] [3] [4] [5] [6] [7]
d
p
1
0
-
6
1
2
1
16
1
-
-
-
-
14
1
1 3
5
3
10
3
1 3 5
4 7
9
5
6
36

(4)
1
2
3
4
5
6
7
2
6
16
7
8
10
3
14
4
4
5 3
1
[1] [2] [3] [4] [5] [6] [7]
d
p
1
0
-
6
1
2
1
9
5
-
-
-
-
14
1
1 3
5
3
10
3
1 3 5
1 2
4
9
37

(5)
1
2
3
4
5
6
7
2
6
16
7
8
10
3
14
4
4
5 3
1
[1] [2] [3] [4] [5] [6] [7]
d
p
1
0
-
6
1
2
1
9
5
-
-
-
-
14
1
1 3
5
3 3
1 3 5
1 2
1 3 5 4
7
12
4
1
0
38

(6)
1
2
3
4
5
6
7
2
6
16
7
8
10
3
14
4
4
5 3
1
[1] [2] [3] [4] [5] [6] [7]
d
p
0
-
6
1
2
1
9
5
-
-
-
-
14
1
5
3
10
3
12
4
1 3 6
7
11
6
39

TOPICS COVERED ARE:
 Backtracking
 Divide and conquer
 Greedy Methods
 Short path algorithm
40

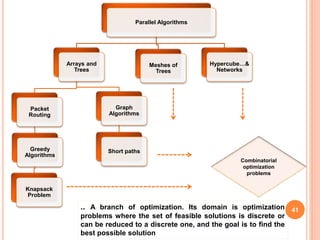
Parallel Algorithms
Arrays and
Trees
Packet
Routing
Greedy
Algorithms
Knapsack
Problem
Graph
Algorithms
Short paths
Meshes of
Trees
Hypercube…&
Networks
Combinatorial
optimization
problems
41
.. A branch of optimization. Its domain is optimization
problems where the set of feasible solutions is discrete or
can be reduced to a discrete one, and the goal is to find the
best possible solution

USE OF ALGORITHMS IN PARALLEL
 With Parallelism many Problems appeared , some
are those of choice of granularity such as Grouping
of tasks or partitioning, scheduling.. And when the
physical architecture is to be taken into account we
face the Mapping problem.
 Greedy Methods Packet routing
 Routes every packets to its destination through the
shortest path.
 Shortest path  Graph algorithms
 To compute the least weight directed path between any
two nodes in a weighted graph.
42

 Branch and Bound Exact Methods
 ..Based on exploring all possible solutions. In theory it
gives optimal solutions but in practice it can be costly an
unusable for large problems.
 It uses B&B in Mapping Problem:
 A mapping, is an application allocation which associate a
processor with a task.
 The B&B algorithms will involve mapping a task
progressively between processors by scanning a search
tree that gives all possible combinations. For each mapping
a partial solution is given and for each one a set of less
restricted partial solutions is constructed similarly by
mapping a second task and so on until all the tasks have
been mapped(leaves of the tree are reached). For each
node the cost of mapping is computed then all branches
can be pruned through an estimating function and he best
computed mapping is then choosed. 43
USE OF ALGORITHMS IN PARALLEL

Q & A
BRANCH AND BOUND VS. BACKTRACKING?
 B&B is An enhancement of backtracking
 Similarity
 A state space tree is used to solve a problem.
 Difference
 The branch-and-bound algorithm does not limit us to any particular way
of traversing the tree and is used only for optimization problems
 The backtracking algorithm requires traversing the tree and is used for
non-optimization problems as well.
44

REFERENCES
 Parallel Algorithms and Architectures ,by Michel
Cosnard, Denis Trystram.
 Parallel and sequential algorithms..
 Greedy Method and Compression, Goodrich
Tamassia
 http://www.wikipedia.org/
45

Parallel_Algorithms_In_Combinatorial_Optimization_Problems.ppt

More Related Content

Similar to Parallel_Algorithms_In_Combinatorial_Optimization_Problems.ppt (20)

Recently uploaded (20)

Parallel_Algorithms_In_Combinatorial_Optimization_Problems.ppt