Performance Characteristics of Hydraulic Machines Vol 1.pptx

MC 371
Hydraulic Machinery
Dr. Clement A. Komolafe
cakomolafe@umat.edu.gh
Recommended textbook
 Fluid Machinery: Application, Selection and Design by Wright
T. and Gerhart P.M.

Lecture content
2
PERFORMANCE CHARACTERISTICS OF
TURBOMACHINES
Dimensional Analysis and Similarity for Turbomachinery:
 Dimensionality
 Similitude
 Dimensionless numbers and -products
 Dimensionless performance variables and similarity for
turbomachinery
 Specific speed and specific diameter

3
Introduction
• Two flow parameters that are very important in all
turbomachines are:
- Flow rate (Q) and,
- Head (H).
• Mechanical quantities associated with the machines are the
- Power (P),
- Speed (N),
- Size (D) and
- Efficiency ()

4
Introduction
The output of a pump
running at a given speed is
the flow rate delivered and
the head developed.
Plot of head (H) versus
flow rate (Q) at constant
speed (N) forms the
fundamental performance
characteristic of a pump.
Plots of power input
required (P) and efficiency
() versus flow rate Q is
also useful.
Typical pump performance
characteristic at a particular speed, N:
H vs. Q for various values of N
P vs. Q
 vs. Q

5
Introduction
In the case of turbines, the output is power developed (P) at a
given speed (N). Fundamental turbine characteristic consists of a
plot of:
Power (P) against speed (N) at constant head (H),
Power (P) against flow rate (Q) and
Efficiency () versus speed (N) is also useful.
Performance characteristics are the relationships between
variables relevant to hydraulic machine in graphical form.
Performance characteristics are determined experimentally by
performances tests. The performance characteristic differs for
different design features and different sizes.

6
Dimensional Analysis
It is a mathematical technique which makes use of the study of
the dimensions for solving several engineering problems. Each
physical phenomenon can be expressed by an equation which
defines the given relation and dimensions, which can be non-
dimensionalized.
Uses of dimensional analysis
1. To test the dimensional homogeneity of any equation of
fluid motion.
2. To derive rational formula for a flow phenomenon.
3. To derive equation expressed in terms of non-dimensional
parameters.
4. To plan model test and present experimental results in a
systematic manner, it makes it possible to analyse the
complex fluid flow problem.

7
Advantages of dimensional analysis
1. It expresses the fundamental relationship between the variables in
dimensionless terms.
2. By the proper selection of variables, the dimensionless
parameters can be used to make certain logical deduction about
the problem.
3. It enables getting a theoretical equation in a simplified
dimensional form.
4. Dimensional analysis provides partial solution to the problems
that are too complex to be dealt with mathematically.
5. The conversion of units of quantities from one system to another
is facilitated.

8
Dimensions
The various physical quantities using fluid phenomenon can be
expressed in terms of fundamental quantities which include; mass,
length, time and temperature, designated by the letters M, L, T and
 respectively.
Dimensionless Groups for Turbomachines Performance
There are three methods to obtain dimensionless groups:
1. Dimensional analysis,
2. Dynamic similarity,
3. Non-dimensionalization of relevant differential equation.

 The concept of dimensional analysis (DA)
i. is closely linked to the principle of dimensional homogeneity,
ii. is important for the correct design of experiments, and
iii. helps in the extraction of maximum possible information from a large
number of test data.
 Applying the concept of dimensional analysis to turbomachines
i. provides a greater depth of understanding to the performance
and classifications of machines,
ii.allows the extrapolation of performance data from one operating
condition to another, and
iii.clarifies the fundamental reasons behind wide configuration
difference in machines.
DIMENSIONALITY
9
Ultimately, one can save a lot of time and money during
designing, testing and analysis in turbomachinery by DA.

 The principle of dimensional homogeneity states that if an equation
correctly represents a relationship between variables in a physical process, it
will be homogeneous in dimensions. That is each term will add to the
other terms only if they are all of like dimensions.
PRINICIPE OF DIMENSIONAL HOMOGENEITY
10
 Consider the familiar Bernoulli equation for a steady, incompressible,
frictionless flow without any shaft work (Eq. 1).
𝑝+𝜌
𝑉 2
2
+𝜌 𝑔𝑧=𝑝0
(1)
Thermodynamic
(or static)
pressure
Dynamic pressure
Hydrostatic
pressure
Stagnation (or total)
pressure

 The concept of similitude allows the variables of problems to be
arranged into dimensionless groups also called dimensionless numbers.
SIMILITUDE OR PRINICIPE OF SIMILARITY
11
 The case of a gas flow in which the hydrostatic term is negligible for
Bernoulli equation may be grouped into a dimensionless number (Eq. 2)
𝑝0 −𝑝
1/2 𝜌 𝑉
2
=1 (2)
 Eq. 2 is known as the pressure coefficient.
 The principle of similarity is used in relating information obtained
from the test of a model to the information that would pertain to the
full scale device, often called the prototype.
 For this to happen there must be geometric similarity, kinematic similarity
and dynamic similarity.
A model and a prototype are geometrically similar if all physical or
body dimensions in all three (Cartesian) axes have the same linear ratio

SIMILITUDE OR PRINICIPE OF SIMILARITY
12
 Finally for dynamic similarity, the ratios of forces, masses, and energies
must be equal between a model and a prototype, presupposing
geometric and kinematic similarities.
 For kinematic similarity, the motions of two systems are kinematically
similar if similar elements lie at similar locations and similar times.
Geometric similarity is a precondition for kinematic similarity.
Similarity study ensures the accurate prediction of
the performance or behavior of one object (or machine
or test) from information about the performance of a
similar object under a different set of conditions (e.g.,
size, speed, and fluid involved)
 Complete similarity is required for the above to take place but in
practice it is frequently impracticable to achieve.

 The basis for any similarity analysis is a set of dimensionless numbers,
formed from the problem variables, that adequately describe the
phenomenon under study. These numbers are determined by
dimensional analysis.
 There are at least four methods of forming the dimensionless numbers
they include:
i. adapting “standard” dimensionless numbers (e.g. Re and Mach nos.),
ii. by inspection,
iii.by non-dimensionalising the governing equations, and
iv.using the П-product method.
 Let’s review the П-product method
 The objective is to form products from the problem variables that will
yield new dimensionless variables that are fewer in number compared to
the original list.
DIMENSIONLESS NUMBERS AND -PRODUCTS
13

 Consider the lift force on an airfoil, which may represent a simple
model of a compressor or a turbine blade (Fig 1).
DIMENSIONLESS NUMBERS AND -PRODUCTS
14
Fig 1: Lift on an airfoil
 The steps are as follows
1) List and count the variables ()
2) List and count the fundamental units or dimensions ()
3) Select a number of variables as “primary”
4) Form П- products from the primaries plus a remaining variable.

 The flow rate is listed first because it is the primary independent
variable.
 is included as reminder that geometric similitude is imposed.
 The dimensionless ratio, (relative roughness) , has been omitted for
the time being.
DIMENSIONLESS PERFORMANCE VARIABLES AND SIMILARITY
FOR TURBOMACHINERY (INCOMPRESSIBLE FLOW)
15
 The performance of a turbomachine in an incompressible flow may
involve the following variables:
o Q: volume flow rate []
o gH: head (specific energy variable) [] (gH = )
o P: power []
o N: rotational speed []
o D: diameter [L]
o : density []
o : fluid viscosity []
o : diameter ratio (dimensionless)
How many dimensionless
parameters can the above
list be reduced to?

Incompressible Fluid Analysis
Let the turbomachine be a pump
or a hydraulic turbine
Control variable:
Q = flow rate,
N = speed of motor
Fluid properties:
 = fluid properties
m= viscosity
Geometric Variables:
D = Impeller diameter,
• K = bulk modulus of elasticity of
the fluid

17
We can take the net energy transfer per unit mass flow rate gH,
the efficiency, , and power supplied P, as dependent variables.
The relationship between the specific energy (head developed)
as the dependent variable and other independent variables is:

18
Variable Dimension
Potential head, gH L2
T-2
Flow rate, Q L3
T-1
Speed, N T-1
Diameter, D L
Density,  ML-3
Viscosity,  ML-1
T-1
Bulk modulus of
elasticity of the fluid, K
ML-1
T-2
Length ratio, D
l -
Power, P ML2
T-3

19
Substituting the dimensions in eqn. (2) gives:

20
Similarly, if the efficiency and power are taken as the
dependent variable the relationship between the variables
may be written as

21

22
In addition to pressure coefficient, the coefficients popularly used in
model testing are given below:

23
Similarity (Affinity) Laws
For all machines belonging to one
family of geometrically similar
machines, the dimensionless
parameters are the same at
corresponding points of their
characteristics (dynamic
similarity). Since
These laws allow us to
predict the performance of
machine when N or D
varied from a known
performance curve.
Dimensionless head H versus volume Q
characteristics of a centrifugal pump

24
Type Number or Specific Speed or Shape
Number (Ns)

25
Number (Ns)
At the point where efficiency is
maximum for each type of
turbomachine with fixed
geometry we define for
geometrically similar machines:
For a pump, we may
define the type number,
Ns, as

26
Number (Ns)
Note that Ns can be calculated at any point on the
characteristic curve but such values have no practical
interest and only the type number at the design point is
called the specific speed.
The specific duty is referred to as the design point,
which is normally associated with the maximum
efficiency of the machine.
The specific speed at the design point is stated for
pumps in terms of flow rate and head developed as:

27
Recall: Type Number or Specific Speed or Shape
Number (Ns)
Dimensionless Specific Speed, Ns for Pump
 4
3
2
1
2
3
max
max
gh
NQ
Ns 





(20)
Dimensional Specific Speed, Nsp for Pump
4
3
H
Q
N
N SP 
Dimensionless Specific Speed, Ns for Turbine
  4
5
2
1
2
1
4
5
max
2
1
max
gh
NP
P
Nsp






Dimensional Specific Speed, Nsp, for Turbine
4
5
H
P
N
NST 
(21)
(22)
(23)

28
Specific Speed (Ns) Classification of Turbine
Best specific speed range for different type of hydraulic turbines

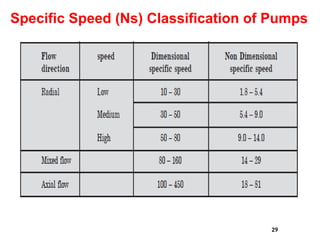
29
Specific Speed (Ns) Classification of Pumps

30
Number (Ns)
Thus, specific speed
relates different types
of pumps without
reference to size.
Broadly speaking,
each different class of
machine has its
optimum efficiency
within a fairly narrow
range of specific
speeds.

31
Number (Ns)
Since, a higher specific
speed implies a smaller
machine, for reasons of
economy, it desirable to
select the highest possible
specific speed consistent
with good efficiency.
With the aid of the type
number, the various
types of pumps and
turbines may be classified
and compared as shown
in the adjacent figure.

32
Number (Ns)

33
Example 1
Francis turbine is required to develop about 4.5 MW at maximum
efficiency when running at 110 rev/min with a head of 14 m. A
scale model is tested with a head of 3.7 m and at maximum
efficiency, the speed was 210 rev/min, the flow rate was 1.45 m3
/s
and the power output was 44.25 kW.
Determine:
(i) the ratio of sizes of turbine and model,
(ii) the specific speed,
(iii) the flow rate required through the turbine,
(iv) the turbine power output, and
(v) the turbine efficiency.

37
Example 2
A quarter-scale turbine model is tested under a head of
11 m. The full-scale turbine is to use a head of 30 m
and to run at 430 rev/min. At what speed should the
model test be made? If, during the test, the model
produces 100 kW at the point of maximum efficiency,
using a flow of 1.08 m3
/s of water, what will be the
power output of the full scale turbine and the flow
rate required at the point of maximum efficiency?

Geometric similarity between a prototype car of
length and a model car of length
 The geometric scale
factor can be less than,
equal to or greater than 1

Kinematic similarity is achieved when, at all locations,
the speed in the model flow is proportional to that at
corresponding locations in the prototype flow, and
points in the same direction.
 Geometric similarity is a
prerequisite for kinematic
similarity.

Correlation of pump impeller shapes with specific speed and diameter

Cordier diagram for all types of turbomachines

Performance Characteristics of Hydraulic Machines Vol 1.pptx

More Related Content

Similar to Performance Characteristics of Hydraulic Machines Vol 1.pptx (20)

More from PenielAnkomah1 (6)

Recently uploaded (20)

Performance Characteristics of Hydraulic Machines Vol 1.pptx

Editor's Notes