![Ppt 2 S1.4Counting particles by mass The mole [Autosaved].pptx](https://image.slidesharecdn.com/ppt2s1-240830135241-76f72799/85/Ppt-2-S1-4Counting-particles-by-mass-The-mole-Autosaved-pptx-14-320.jpg)
![Ppt 2 S1.4Counting particles by mass The mole [Autosaved].pptx](https://image.slidesharecdn.com/ppt2s1-240830135241-76f72799/85/Ppt-2-S1-4Counting-particles-by-mass-The-mole-Autosaved-pptx-31-320.jpg)
![Mole and concentration relationship.
Solutions
Solution a homogeneous mixture of a substance (the
solute) dissolved in another substance (the solvent)
(Molar) concentration (C) is the amount of solute (in
mol) per unit volume (in dm3), often written using [. . . ],
and expressed in moldm-3
Standard solution a solution with a known
concentration of solute](https://image.slidesharecdn.com/ppt2s1-240830135241-76f72799/85/Ppt-2-S1-4Counting-particles-by-mass-The-mole-Autosaved-pptx-39-320.jpg)
Ppt 2 S1.4Counting particles by mass The mole [Autosaved].pptx
- 1. Ppt 2 S1.4 How do we quantify matter on the atomic scale? Structure 1.4 Counting particles by mass: The mole SL &HL Structure 1.4.1 The mole (mol) is the SI unit of amount of substance. One mole contains exactly the number of elementary entities given by the Avogadro constant. Convert the amount of substance, n, to the number of specified elementary entities. SL &HL Structure 1.4.2 Masses of atoms are compared on a scale relative to 12C and are expressed as relative atomic mass Ar and relative formula mass Mr . Determine relative formula masses Mr from relative atomic masses Ar . SL &HL Structure 1.4.3 Molar mass M has the units g mol–1. SL &HL Structure 1.4.4 The empirical formula of a compound gives the simplest ratio of atoms of each element present in that compound. The molecular formula gives the actual number of atoms of each element present in a molecule. SL &HL Structure 1.4.5 The molar concentration is determined by the amount of solute and the volume of solution. SL &HL Structure 1.4.6 Avogadro’s law states that equal volumes of all gases measured under the same conditions of temperature and pressure contain equal numbers of molecules.
- 4. Balancing equation: Law of conservation of mass
- 5. Half equations and Reaction conditions
- 6. The mole Concept WHAT IS A MOLE ? it is the standard unit of amount of a substance containing 6.02 x 1023 Particles SINGLE for 1 PAIR for 2 DOZEN for 12 SCORE for 20 GROSS for 144 CENTURY for 100 1 MOLE for ? 1 MOLE for 6.02 x 1023 It is also known as... AVOGADRO’S NUMBER (NA) AVOGADRO’S CONSTANT The mole connects the macro world that we can measure with the
- 7. Mole Relationship: Mass, Number of particles, volume and concentration
- 8. Moles and Number of particles 1 MOLE Contains 6.02 x 10 23 Particles ( Molecules, atoms, ions or electrons ) n = Moles = Number of particles / Avogadro’s number Example: How many a) molecules of H2O are in 3 moles of water? 1 Mole = Avogadro's constant molecues Therefore 3 moles = ? (3x Avogadro's constant)/1 = 3X 6.02 x 1023 =1.806 X 10 24 molecules How many b) hydrogen atoms in 3 moles of water? 1 molecule has 2 hydrogen atoms Therefore 1.806 X 10 24 molecules have 2 x 1.806 X 1024 = 3.612 X 1024 hydrogen atoms
- 9. Practice questions 1 Calculate the number of atoms in each of the following amounts: a. 1.004 mol bismuth b. 2.5 mol manganese c. 0.000 000 2 mol helium d. 32.6 mol strontium Answers a. ans: 6.046 1023 atoms Bi b. 1.5 1024 atoms Mg c. ans: 1 1017 atoms He d. ans: 1.96 1025 atoms Sr
- 10. Practice questions 2 2. Calculate the amount in moles in each of the following quantities: a. 3.01 1023 atoms of rubidium b. 8.08 1022 atoms of krypton c. 5 700 000 000 atoms of lead d. 2.997 1025 atoms of vanadium Answers a. 3.01 1023 atoms of rubidium ans: 0.500 mol Rb b. 8.08 1022 atoms of krypton ans: 0.134 mol Kr c. 5 700 000 000 atoms of lead ans: 9.5 1015 mol Pb d. 2.997 1025 atoms of vanadium ans: 49.77 mol V
- 11. Practice Question 3 How many Molecules( formula units) in 2.50 moles of Aluminum sulphate? How many total atoms in 2.50 moles of Aluminum sulphate? How many number of cations in 2.50 moles of Aluminum sulphate? How many number of anions in 2.50 moles of Aluminum sulphate? Use m/Mr = No/NA
- 12. If P = Phosphorous What is the difference between P4 and 4P? P4 = 1molecule composed of 4 atoms of Phosphorous 4P = four atoms of phosphorous
- 13. Mole and Formula mass /Molecular mass Relation Individual atoms and molecules are extremely small. Hence a larger unit is appropriate for measuring quantities of matter. The formula mass is the sum of atomic masses in a formula. ( applies to ioninc compounds) If the formula is a molecular formula, then the formula mass may also be called a molecular mass. If the formula mass is expressed in grams it is called a gram formula mass. The gram formula mass is also known as the Molar Mass. The molar mass is the number of grams necessary to make 1 mole of a substance. The units for Molar Mass are g mol-1 . The Relative atomic mass Ar is the weighted average of the masses of all isotopes of an element compared on scale relative to C-12 ( has no units) The Relative molecular mass Mr is the sum of the masses of the atoms in a molecule compared on scale relative to C-12 ( has no units)
- 15. Mole and Mass 1 mole of a substance has a mass equal to the formula mass in grams. Examples 1 mole H2O is the number of molecules in 18.02 g H2O 1 mole H2 is the number of molecules in 2.02 g H2. 1 mole of atoms has a mass equal to the atomic weight in grams. 1 mole of particles = 6.02 x 1023 particles for any substance! The Molar mass is the mass of one mole of a substance Example: Molar Mass of H2O From the Periodic Table - Atomic Masses: H =1.01, O = 16.00 The formula mass / Molecular mass = 2(1.01)+16.00 = 18.02 Molar mass = 18.02 g mol-1 n(mol) =
- 16. Calculate formula /Molecular mass of the following Calculate the gram formula mass or Molar Mass of Na3PO4. Calculate molecular mass of the following: Ca(OH)2 Sulphuric Acid Copper(II) sulphate pentahydrate Nitrogen gas Ammonia (NH3)
- 17. CALCULATING THE NUMBER OF MOLES OF A SINGLE SUBSTANCE moles = mass / molar mass mass = moles x molar mass molar mass = mass / moles UNITS mass g molar mass g mol-1 Calculate the following: 1) What is the mass of 0.25 mol of Na2CO3 ? 2) Calculate the number of moles of oxygen molecules in 4.00 g oxygen molecules have the formula O2 MOLE and Mass Relation MOLES = MASS MOLAR MASS MASS MOLES x MOLAR MASS COVER UP THE VALUE YOU WANT AND THE METHOD OF CALCULATION IS REVEALED
- 19. Percentage Composition According to the law of definite proportions, compounds, contain definite proportions of each element by mass. The sum of all of the atomic masses of elements in a formula is called the formula mass. If it is expressed in grams, then it is called a gram formula mass or molar mass. If it represents the sum of all of the masses of all of the elements in a molecule then it is called a molecular mass. To find the percentage of each element in a compound it is necessary to compare the total mass of each element with the formula mass. 19
- 20. Percentage Composition The percent by mass of each element in a compound is equal to the percentage that its atomic mass is of the formula mass. Example: Calculate the percentage of oxygen in potassium chlorate, KClO3 Atomic masses: K = 39.09, Cl = 35.45 and O = 16.00. Formula mass = 39.09 + 35.45+ 3(16.00) = 122.54 Percent Oxygen = (3(16.00)/122.54) (100) = 39.17% 20
- 21. Calculate the percentage by mass of each element in potassium carbonate, K2CO3
- 22. Calculate the percentage by mass of each element in potassium carbonate, K2CO3 First calculate the formula mass for K2CO3 . Find the atomic mass of each element from the periodic table. Multiply it by the number of times it appears in the formula and add up the total 2 Potassium atoms K 2 x 39.10 = 78.20 1 carbon atom C 1 x 12.01 = 12.01 3 Oxygen atoms O 3 x 16.00 = 48.00 Total = 138.21 To find the percent of each element divide the part of the formula mass that pertains to that element with the total formula mass Percent of Potassium K = 78.20 X 100 =56.58 % 138.21 Percent of Carbon C = 12.01 X 100 = 8.69 % 138.21 Percent of Oxygen O = 48.00 X 100 = 34.73 % 138.21
- 23. Practice question 5 Fertilizers containing larger total % of NPK are considered as good fertilizers. Which of the following can be good fertilizer? Ammonium Phosphate Urea CO(NH2)2
- 24. Empirical Formula Determination The empirical formula is the simplest ratio of the numbers of atoms of each element that make a compound. To find the empirical formula of a compound: 1. Divide the amount of each element (either in mass or percentage) by its atomic mass. This calculation gives you moles of atoms for each element that appears in the formula 2. Convert the results to small whole number ratios. Often the ratios are obvious. If they are not divide all of the other quotients by the smallest quotient 24
- 25. Example 1 Analysis of a certain compound showed that 39.356 grams of compound contained 0.883 grams of hydrogen, 10.497 grams of Carbon, and 27.968 grams of Oxygen. Calculate the empirical formula of the compound. 25
- 26. First divide the amount by the atomic mass to get the number of moles of each kind of atom in the formula Hydrogen H = 0.883 g = 0.874 mol 1.01 g mol-1 Carbon C = 10.497 g = 0.874 mol 12.01 g mol-1 Oxygen O = 27.968 g = 1.748 mol 16.00 g mol-1 Analysis of the ratio s shows that the first two are identical and that the third is twice the other two. Therefore the ratio of H to C to O is 1 to 1 to 2. The empirical formula is HCO2
- 27. Molecular Formula To calculate the molecular formula from the empirical formula it is necessary to know the molecular (molar) mass. Add up the atomic masses in the empirical formula to get the factor Divide this number into the molecular formula mass. If the number does not divide evenly you probably have a mistake in the empirical formula or its formula mass Multiply each subscript in the empirical formula by the factor to get the molecular formula 27
- 28. Molecular Formula Example Example: Suppose the molecular mass of the compound in the previous example, HCO2 is 90.0. Calculate the molecular formula. The empirical formula mass of is 1 H 1.01 x 1 = 1.01 1 C 12.0 x 1 = 12.00 2 O 16.0 x 2 = 32.00 Total 45.01 Note that 45 is exactly half of the molecular mass of 90. So the formula mass of HCO2 is exactly half of the molecular mass. Hence the molecular formula is double that of the empirical formula or H2C2O4 28
- 29. Structural formula. H2C2O4 is organic acid. Draw structural formula.
- 30. Write empirical formula for the following:
- 32. Example: Exercise: Naphthalene, best known as ‘mothballs’, is composed of carbon (93.71%) and hydrogen (6.29%). If the molar mass of the compound is 128g, what is the molecular formula of naphthalene? carbon hydrogen mass of element 93.71 6.29 number of moles 93.71/12 = 7.8 6.29/ 1 = 6.29 DO NOT ROUND UP OR DOWN most simple ratio 7.8/ 6.29 = 1.25 6.29/6.29 = 1 AGAIN DO NOT ROUND UP OR DOWN BUT FIND LOWEST WHOLE NUMBER RATIO lowest whole number ratio 5 4 empirical formula: C5H4 ratio molecular formula /empirical formula: 128g/ 64g = 2 molecular formula = 2 x C5H4 = C10H8
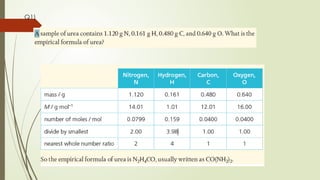
- 33. Q1)
- 34. Q2) Experimental question: Find the empirical formula of oxide of Magnesium. Suggest the possible errors in the experiment
- 35. Solution 2 )
- 36. Q3)
- 37. Challenge
- 38. Simulation lab: Water of hydration Play the following video for 1:57 minutes to calculate water of hydration in hydrated copper(II) sulphate sample https://www.youtube.com/watch?v=OuF4hjTFdsg
- 39. Mole and concentration relationship. Solutions Solution a homogeneous mixture of a substance (the solute) dissolved in another substance (the solvent) (Molar) concentration (C) is the amount of solute (in mol) per unit volume (in dm3), often written using [. . . ], and expressed in moldm-3 Standard solution a solution with a known concentration of solute
- 40. Solute concentration is independent of solvent volume
- 41. CALCULATING THE NUMBER OF MOLES OF SOLUTE IN A SOLUTION UNITS concentration mol dm-3 volume dm3 BUT IF... concentration mol dm-3 volume cm3 THE MOLE MOLES CONC x VOLUME COVER UP THE VALUE YOU WANT AND THE METHOD OF CALCULATION IS REVEALED MOLES = CONCENTRATION x VOLUME MOLES = CONCENTRATION (mol dm-3 ) x VOLUME (dm3 ) MOLES = CONCENTRATION (mol dm-3 ) x VOLUME (cm3 ) 1000
- 42. Units of concentration of solution
- 43. Use n=CV or m/Mr = CV
- 44. Practice questions Calculate the number of moles of sodium hydroxide in 25 cm3 of 2M NaOH
- 46. The original solution has a concentration of 0.100 mol dm-3 This means that there are 0.100 mols of solute in every 1 dm3 (1000 cm3 ) of solution Take out 25.00 cm3 and you will take a fraction 25/1000 or 1/40 of the number of moles moles in 1dm3 (1000cm3 ) = 0.100 moles in 1cm3 = 0.100/1000 moles in 25cm3 = 25 x 0.100/1000 = 2.5 x 10-3 mol 250cm3 25cm3 250cm3 CALCULATING THE NUMBER OF MOLES OF SOLUTE IN A SOLUTION concentration of solution in the graduated flask = 0.100 mol dm-3 volume pipetted out into the conical flask = 25.00 cm3 Moles in part of the solution
- 47. Converting mol/dm3 g/dm3 • to convert from mol/dm3 to g/dm3 , multiply by the relative formula mass • to convert from g/dm3 to mol/dm3 , divide by the relative formula mass • Calculate the concentration of 0.1 mol/dm3 sodium hydroxide solution in g/dm3 . (Mr of NaOH = 40) • Calculate the concentration of 7.3 g/dm3 hydrochloric acid in mol/dm3 . (Mr of HCl = 36.5) • 100 cm3 of dilute hydrochloric acid contains 0.02 mol of dissolved hydrogen chloride. Calculate the concentration of the acid in g/dm3 .
- 48. Standard solution: Solution whose concentration is known accurately ( Activity on preparation of standard solution)
- 49. Dilution of a solution C1V1 = C2V2
- 50. Titration: A titration is a technique where a solution of known concentration is used to determine the concentration of an unknown solution. Acid-base Titrations. Redox Titrations. Precipitation Titrations. Complexometric Titrations.
- 51. Q1
- 53. Challenge Q1 and Q2
- 54. Molar gas volume Room temperature and pressure (RTP) is defined as 25o C (298.15K)and 1atm(100kPa) pressure. The molar volume of a gas is the volume of one mole of a gas at STP. At STP, one mole of any gas occupies a volume of 24 dm3 ! Molar volume of any gas at RTP occupies 24 dm3 Standard temperature and pressure (STP) is defined as 0o (273.15K)and 1atm(100kPa) pressure. The molar volume of a gas is the volume of one mole of a gas at STP. At STP, one mole of any gas occupies a volume of 22.7 dm3 ! Molar volume of any gas at STP occupies 22.7 dm3 (0.0227 m3 mol-1 )
- 56. Molar volume
- 57. Avogadro’s Law: Directly relates gas volumes to moles
- 58. Quick questions
- 61. Revise Watch series of video https://www.youtube.com/watch?v=sM4ulTjsuA4&list=PL816Qsrt2Os1gF8vAO0 BlZZpgykuhaCIk&index =1