Quality Management with Detailed Version.ppt

Quality Management
Quality Management
“
“It costs a lot to produce a bad product.
It costs a lot to produce a bad product.”
”
Norman Augustine
Norman Augustine

Cost of quality
1. Prevention costs
2. Appraisal costs
3. Internal failure costs
4. External failure costs
5. Opportunity costs

What is quality management all about?
Try to manage all aspects of the organization
in order to excel in all dimensions that are
important to “customers”
Two aspects of quality:
features: more features that meet customer needs
= higher quality
freedom from trouble: fewer defects = higher
quality

The Quality Gurus – Edward Deming
1900-1993
1986
Quality is
“uniformity and
dependability”
Focus on SPC
and statistical
tools
“14 Points” for
management
PDCA method

The Quality Gurus – Joseph Juran
1904 - 2008
1951
Quality is
“fitness for use”
Pareto Principle
Cost of Quality
General
management
approach as well
as statistics

History: how did we get here…
• Deming and Juran outlined the principles of Quality
Management.
• Tai-ichi Ohno applies them in Toyota Motors Corp.
• Japan has its National Quality Award (1951).
• U.S. and European firms begin to implement
Quality Management programs (1980’s).
• U.S. establishes the Malcolm Baldridge National
Quality Award (1987).
• Today, quality is an imperative for any business.

What does Total Quality Management encompass?
TQM is a management philosophy:
• continuous improvement
• leadership development
• partnership development
Cultural
Alignment
Technical
Tools
(Process
Analysis, SPC,
QFD)
Customer

Developing quality specifications
Input Process Output
Design Design quality
Dimensions of quality
Conformance quality

Six Sigma Quality
• A philosophy and set of methods companies use to
eliminate defects in their products and processes
• Seeks to reduce variation in the processes that lead to
product defects
• The name “six sigma” refers to the variation that
exists within plus or minus six standard deviations of
the process outputs

6


Six Sigma Roadmap (DMAIC)
Next Project Define
Customers, Value, Problem Statement
Scope, Timeline, Team
Primary/Secondary & OpEx Metrics
Current Value Stream Map
Voice Of Customer (QFD)
Measure
Assess specification / Demand
Measurement Capability (Gage R&R)
Correct the measurement system
Process map, Spaghetti, Time obs.
Measure OVs & IVs / Queues
Analyze (and fix the obvious)
Root Cause (Pareto, C&E, brainstorm)
Find all KPOVs & KPIVs
FMEA, DOE, critical Xs, VA/NVA
Graphical Analysis, ANOVA
Future Value Stream Map
Improve
Optimize KPOVs & test the KPIVs
Redesign process, set pacemaker
5S, Cell design, MRS
Visual controls
Value Stream Plan
Control
Document process (WIs, Std Work)
Mistake proof, TT sheet, CI List
Analyze change in metrics
Value Stream Review
Prepare final report
Validate
Project $
Validate
Project $
Validate
Project $
Validate
Project $
Celebrate
Project $

Quality Improvement
Traditional
Continuous Improvement
Time
Quality

Continuous improvement philosophy
1. Kaizen: Japanese term for continuous improvement.
A step-by-step improvement of business processes.
2. PDCA: Plan-do-check-act as defined by Deming.
Plan Do
Act Check
3. Benchmarking : what do top performers do?

Tools used for continuous improvement
1. Process flowchart

2. Run Chart
Performance
Time

3. Control Charts
Performance Metric
Time

4. Cause and effect diagram (fishbone)
Environment
Machine Man
Method Material

5. Check sheet
Item A B C D E F G
-------
-------
-------
√ √ √
√ √
√ √
√
√
√ √
√ √ √
√
√
√
√
√ √

6. Histogram
Frequency

7. Pareto Analysis
A B C D E F
Frequency
Percentage
50%
100%
0%
75%
25%
10
20
30
40
50
60

Summary of Tools
1. Process flow chart
2. Run diagram
3. Control charts
4. Fishbone
5. Check sheet
6. Histogram
7. Pareto analysis

Case: shortening telephone waiting time…
• A bank is employing a call answering service
• The main goal in terms of quality is “zero waiting time”
- customers get a bad impression
- company vision to be friendly and easy access
• The question is how to analyze the situation and improve quality

The current process
Custome
r B
Operator
Custome
r A
Receiving
Party
How can we reduce
waiting time?

Makes
custome
r wait
Absent receiving
party
Working system of
operators
Customer Operator
Fishbone diagram analysis
Absent
Out of office
Not at desk
Lunchtime
Too many phone calls
Absent
Not giving receiving
party’s coordinates
Complaining
Leaving a
message
Lengthy talk
Does not know
organization well
Takes too much time to
explain
Does not
understand
customer

Daily
average
Total
number
A One operator (partner out of office) 14.3 172
B Receiving party not present 6.1 73
C No one present in the section receiving call 5.1 61
D Section and name of the party not given 1.6 19
E Inquiry about branch office locations 1.3 16
F Other reasons 0.8 10
29.2 351
Reasons why customers have to wait
(12-day analysis with check sheet)

Pareto Analysis: reasons why customers have to wait
A B C D E F
Frequency Percentage
0%
49%
71.2%
100
200
300 87.1%
150
250

Ideas for improvement
1. Taking lunches on three different shifts
2. Ask all employees to leave messages when leaving desks
3. Compiling a directory where next to personnel’s name
appears her/his title

Results of implementing the recommendations
A B C D E F
100%
0%
49%
71.2%
100
200
300 87.1%
100%
B C A D E F
0%
100
200
300
Before… …After
Improvement

In general, how can we monitor quality…?
1. Assignable variation: we can assess the cause
2. Common variation: variation that may not be possible to
correct (random variation, random noise)
By observing
variation in
output measures!

Statistical Process Control (SPC)
Every output measure has a target value and a level of
“acceptable” variation (upper and lower tolerance limits)
SPC uses samples from output measures to estimate the
mean and the variation (standard deviation)
Example
We want beer bottles to be filled with 12 FL OZ ± 0.05 FL OZ
Question:
How do we define the output measures?

In order to measure variation we need…
The average (mean) of the observations:



N
i
i
x
N
X
1
1
The standard deviation of the observations:
N
X
x
N
i
i



 1
2
)
(


Average & Variation example
Number of pepperoni’s per pizza: 25, 25, 26, 25, 23, 24, 25, 27
Average:
Standard Deviation:
Number of pepperoni’s per pizza: 25, 22, 28, 30, 27, 20, 25, 23
Average:
Standard Deviation:
Which pizza would you rather have?

When is a product good enough?
Incremental
Cost of
Variability
High
Zero
Lower
Tolerance
Target
Spec
Upper
Tolerance
Traditional View
The “Goalpost” Mentality
a.k.a
Upper/Lower Design Limits
(UDL, LDL)
Upper/Lower Spec Limits
(USL, LSL)
Upper/Lower Tolerance Limits
(UTL, LTL)

But are all ‘good’ products equal?
Incremental
Cost of
Variability
High
Zero
Lower
Spec
Target
Spec
Upper
Spec
Taguchi’s View
“Quality Loss Function”
(QLF)
LESS VARIABILITY implies BETTER PERFORMANCE !

Capability Index (Cpk)
It shows how well the performance measure
fits the design specification based on a given
tolerance level
A process is k capable if
LTL
k
X
UTL
k
X 


 
 and
1
and
1 




 k
LTL
X
k
X
UTL

Capability Index (Cpk)
Cpk < 1 means process is not capable at the k level
Cpk >= 1 means process is capable at the k level





 



 k
X
UTL
k
LTL
X
Cpk ,
min
Another way of writing this is to calculate the capability index:

Accuracy and Consistency
We say that a process is accurate if its mean is close to
the target T.
We say that a process is consistent if its standard deviation
is low.
X

Example 1: Capability Index (Cpk)
X = 10 and σ = 0.5
LTL = 9
UTL = 11
667
.
0
5
.
0
3
10
11
or
5
.
0
3
9
10
min 











pk
C
UTL
LTL X

X = 9.5 and σ = 0.5
LTL = 9
UTL = 11
UTL
LTL X

X = 10 and σ = 2
LTL = 9
UTL = 11
UTL
LTL X

Example
Consider the capability of a process that puts
pressurized grease in an aerosol can. The design
specs call for an average of 60 pounds per square
inch (psi) of pressure in each can with an upper
tolerance limit of 65psi and a lower tolerance limit
of 55psi. A sample is taken from production and it
is found that the cans average 61psi with a standard
deviation of 2psi.
1. Is the process capable at the 3 level?
2. What is the probability of producing a defect?

Solution
LTL = 55 UTL = 65  = 2
61

X
6667
.
0
)
6667
.
0
,
1
min(
)
6
61
65
,
6
55
61
min(
)
3
,
3
min(








pk
pk
C
X
UTL
LTL
X
C


No, the process is not capable at the 3 level.

Solution
P(defect) = P(X<55) + P(X>65)
=P(X<55) + 1 – P(X<65)
=P(Z<(55-61)/2) + 1 – P(Z<(65-61)/2)
=P(Z<-3) + 1 – P(Z<2)
=G(-3)+1-G(2)
=0.00135 + 1 – 0.97725 (from standard normal table)
= 0.0241
2.4% of the cans are defective.

Example (contd)
Suppose another process has a sample mean of 60.5 and
a standard deviation of 3.
Which process is more accurate? This one.
Which process is more consistent? The other one.

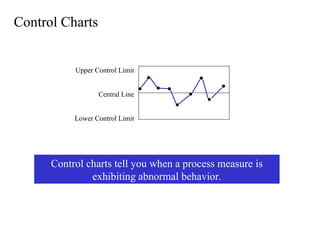
Control Charts
Control charts tell you when a process measure is
exhibiting abnormal behavior.
Upper Control Limit
Central Line
Lower Control Limit

Two Types of Control Charts
• X/R Chart
This is a plot of averages and ranges over time
(used for performance measures that are variables)
• p Chart
This is a plot of proportions over time (used for
performance measures that are yes/no attributes)

When should we use p charts?
1. When decisions are simple “yes” or “no” by inspection
2. When the sample sizes are large enough (>50)
Sample (day) Items Defective Percentage
1 200 10 0.050
2 200 8 0.040
3 200 9 0.045
4 200 13 0.065
5 200 15 0.075
6 200 25 0.125
7 200 16 0.080
Statistical Process Control with p Charts

Let’s assume that we take t samples of size n …
size)
(sample
samples)
of
number
(
defects"
"
of
number
total


p
n
p
p
sp
)
1
( 

p
p
zs
p
LCL
zs
p
UCL





066
.
0
15
1
200
6
80




p
017
.
0
200
)
066
.
0
1
(
066
.
0



p
s
015
.
0
017
.
0
3
066
.
0
117
.
0
017
.
0
3
066
.
0








LCL
UCL

LCL = 0.015
UCL = 0.117
p = 0.066

When should we use X/R charts?
1. It is not possible to label “good” or “bad”
2. If we have relatively smaller sample sizes (<20)
Statistical Process Control with X/R Charts

Take t samples of size n (sample size should be 5 or more)



n
i
i
x
n
X
1
1
}
{
min
}
{
max i
i x
x
R 

R is the range between the highest and the lowest for each sample
X is the mean for each sample




t
j
j
X
t
X
1
1



t
j
j
R
t
R
1
1
X is the average of the averages.
R is the average of the ranges

R
A
X
LCL
R
A
X
UCL
X
X
2
2




define the upper and lower control limits…
R
D
LCL
R
D
UCL
R
R
3
4


Read A2, D3, D4 from
Table TN 8.7

Example: SPC for bottle filling…
Sample Observation (xi) Average Range (R)
1 11.90 11.92 12.09 11.91 12.01
2 12.03 12.03 11.92 11.97 12.07
3 11.92 12.02 11.93 12.01 12.07
4 11.96 12.06 12.00 11.91 11.98
5 11.95 12.10 12.03 12.07 12.00
6 11.99 11.98 11.94 12.06 12.06
7 12.00 12.04 11.92 12.00 12.07
8 12.02 12.06 11.94 12.07 12.00
9 12.01 12.06 11.94 11.91 11.94
10 11.92 12.05 11.92 12.09 12.07

Example: SPC for bottle filling…
Sample Observation (xi) Average Range (R)
1 11.90 11.92 12.09 11.91 12.01 11.97 0.19
2 12.03 12.03 11.92 11.97 12.07 12.00 0.15
3 11.92 12.02 11.93 12.01 12.07 11.99 0.15
4 11.96 12.06 12.00 11.91 11.98 11.98 0.15
5 11.95 12.10 12.03 12.07 12.00 12.03 0.15
6 11.99 11.98 11.94 12.06 12.06 12.01 0.12
7 12.00 12.04 11.92 12.00 12.07 12.01 0.15
8 12.02 12.06 11.94 12.07 12.00 12.02 0.13
9 12.01 12.06 11.94 11.91 11.94 11.97 0.15
10 11.92 12.05 11.92 12.09 12.07 12.01 0.17
Calculate the average and the range for each sample…

Then…
00
.
12

X
is the average of the averages
15
.
0

R
is the average of the ranges

Finally…
91
.
11
15
.
0
58
.
0
00
.
12
09
.
12
15
.
0
58
.
0
00
.
12








X
X
LCL
UCL
Calculate the upper and lower control limits
0
15
.
0
0
22
.
1
15
.
0
11
.
2






R
R
LCL
UCL

LCL = 11.90
UCL = 12.10
The X Chart
X = 12.00

The R Chart
LCL = 0.00
R = 0.15
UCL = 0.32

The X/R Chart
LCL
UCL
X
LCL
R
UCL
What can you
conclude?

Quality Management with Detailed Version.ppt

More Related Content

Similar to Quality Management with Detailed Version.ppt (20)

Recently uploaded (20)

Quality Management with Detailed Version.ppt