Random variables.pptx
- 1. PROBABILITY AND RANDOM PROCESS
- 2. Random Variables A random variable is a function that assigns a real number X(s) to every elements s in S, where S is the sample space corresponding to a random experiment. Random variables Discrete Random Variables Continuous Random variables Dr. S. Kalyani PRP 2
- 3. Discrete Random variable: If X is a random variable which can take a finite number or countably infinite number of values, X is called a Discrete Random variable. Eg: 1. The marks obtained by the student in an exam. 2. Number of students absent for a particular class. Continuous Random variable: If X is a random variable which can take all values in an interval, then is called a Continuous Random variable. Eg: The length of time during which a vacuum tube installed in a circuit functions is a continuous RV. Dr. S. Kalyani PRP 3
- 4. Probability Mass Function (or) Probability Function: If X is a discrete RV with distinct values x1 x2 x3 ,… xn… then P ( X = xi) = pi, then the function p(x) is called the Probability Mass Function. Where p(i = 1, 2, 3, …) satisfy the following conditions: 1. for all i, and 2. 0, pi 1 i i p Dr. S. Kalyani PRP 4
- 5. PROBABILITY DENSITY FUNCTION FOR CONTINUOUS CASE: If X is a continuous r.v., then f(x) is defined the probability density function of X. Provided f(x) satisfies the following conditions, 1. 2. 3. ( ) 0 f x ( ) 1 f x dx ( ) ( ) b a P a x b f x dx Dr. S. Kalyani PRP 5
- 6. CUMULATIVE DISTRIBUTION FUNCTION OF C.R.V.: The cumulative distribution function of a continuous r.v. X is ( ) ( ) ( ) , x F x P X x f x dx for x CUMULATIVE DISTRIBUTION FUNCTION OF D.R.V.: The cumulative distribution function F(x) of a discrete r.v. X with probability distribution p(x) is given by ( ) ( ) ( ) i i X x F x P X x p x for x 6 Dr. S. Kalyani PRP
- 7. Dr. S. Kalyani PRP 7 Relationship between probability density function and distribution function 𝑖) 𝑓 𝑥 = 𝑑 𝑑𝑥 𝐹 𝑥 𝑖𝑖) 𝐹 𝑥 = −∞ 𝑥 𝑓 𝑥 𝑑𝑥
- 8. PROBLEM 1: The number of telephone calls received in an office during lunch time has the following probability function given below No. of calls 0 1 2 3 4 5 6 Probability p(x) 0.05 0.2 0.25 0.2 0.15 0.1 0.05 i) Verify that it is really a probability function. ii) Find the probability that there will be 3 or more calls. iii)Find the probability that there will be odd number of calls. Dr. S. Kalyani PRP 8
- 9. ii) Let X denote the no. of telephone calls P(X>=3) = P(X=3) + P(X=4) + P(X=5) +P(X=6) = 0.2 + 0.15 + 0.1 + 0.05 = 0.5 iii) Let X denote the no. of telephone calls P(X is odd) = P(X=1) + P(X=3) + P(X=5) = 0.2 + 0.2 + 0.1 = 0.5 i) Probability function p(x) follows 2 properties i) all probability values lies between 0 and 1 ii) total probability value is 1. In the given data all probability values are between 0 and 1 And 0.05+0.2+0.25+0.15+0.1+0.05 = 1 So it is a probability function. Solution: Dr. S. Kalyani PRP 9
- 10. PROBLEM 2: A r. v. X has the following probability functions X 0 1 2 3 4 5 6 7 p(x) 0 k 2k 2k 3k k2 2k2 7k2 + k Find (i) value of k (ii) P(1.5 < X < 4.5 / X > 2) (iii) if P(X ≤ a) > ½, find the minimum value of a. Dr. S. Kalyani PRP 10
- 11. Solution: 7 0 2 ( ) . . . ( ) 1 10 9 1 (10 1)( 1) 0 1 , 1 10 ( ) cannot be negative, 1 is neglected. 1 10 x i w k t p x k k k k k p x k k Dr. S. Kalyani PRP 11
- 12. 7 3 ( ) (1.5 4.5 / 2) ( ) ( / ) ( ) [(1.5 4.5) ( 2)] (1.5 4.5 / 2) ( 2) ( 3) ( 4) ( ) 5 5 10 = 7 7 10 r ii P X x P A B P A B P B P X X P X X P X P X P X P X r Dr. S. Kalyani PRP 12 0 1 2 3 4 5
- 13. ( ) By trials, ( 0) 0 1 ( 1) 10 3 ( 2) 10 5 ( 3) 10 8 ( 4) 10 1 the minimum value of 'a' satisfying the condition ( ) 4 2 iii P X P X P X P X P X P X a is X 0 1 2 3 4 5 6 7 p(x) 0 1/10 2/10 2/10 3/10 1/100 2/100 17/100 Dr. S. Kalyani PRP 13
- 14. PROBLEM 3 A random Variable X has the following probability distribution. Find (i) the value of k (ii) Evaluate P[X<2] and P[-2<X<2] (iii)Find the cumulative Distribution of X. x -2 -1 0 1 2 3 p(x) 0.1 k 0.2 2k 0.3 3k Dr. S. Kalyani PRP 14
- 15. Solution: Dr. S. Kalyani PRP 15 6 0 ( ) . . . ( ) 1 6 0.6 1 6 0.4 1 15 x i w k t p x k k k
- 16. 2 2 1 0 1 1 2 0.1 0.2 15 15 3 1 0.3 15 2 ii P X P X P X P X P X Dr. S. Kalyani PRP 16
- 17. Dr. S. Kalyani PRP 17 ( ) [ ] [ ] [ ] [ ] 2 2 1 0 1 1 2 0.2 15 15 3 = 0.2 15 2 5 ii P X P X P X P X - < < = = - + = + = = + + + =
- 18. (iii) The Cumulative Distribution of X: X F(x) = P(X ≤ x) -2 F(-2)=P(X≤-2)=P(X=-2)=0.1=1/10 -1 F(-1)=P(X≤-1)=F(-2)+P(-1)=1/10+k=1/10+1/15=0.17 0 F(0)=P(X≤0)=F(-1)+P(0)=1/6+2/10=1/6+1/5=0.37 1 F(1)=P(X≤1)=F(0)+P(1)=11/30+2/15=15/30=1/2 2 F(2)=P(X≤2)=F(1)+P(2)=1/2+3/10=(5+3)/10=8/10=4/5 3 F(3)=P(X≤3)=F(2)+P(3)=4/5+3/15=(12+3)/15=1 Dr. S. Kalyani PRP 18
- 19. Dr. S. Kalyani PRP 19 Problem If the random variable X takes the values 1,2,3 and 4 such that 2P(X=1) = 3P(X=2) = P(X=3) = 5P(X=4), find the probability distribution and cumulative distribution function. Let P(X=3) = k So P(X=1) = k/2 P(X=2) = k/3 P(X=4) = k/5 By property, 𝑘 + 𝑘 2 + 𝑘 3 + 𝑘 5 = 1 So 𝑘 = 30 61
- 20. X 1 2 3 4 P(X) 15/61 10/61 30/61 6/61 Dr. S. Kalyani PRP 20 F(X)= 1 𝑥 𝑝(𝑋) When X < 1 , F(X) = 0 X 1 2 3 4 F(X) 15/61 25/61 55/61 61/61 = 1
- 21. Problem 3: The diameter, say X of an electric cable, is assumed to be a continuous r.v. with p.d.f. : f(x) = 6x(1-x), 0 ≤ x ≤ 1 (i) Check that the above is a p.d.f. (ii) Compute P(X ≤ ½ / ⅓ ≤ X ≤ ⅔) (iii) Determine the number k such that P(X< k) = P(X > k) (iv) Find the cumulative distribution function. Dr. S. Kalyani PRP 21
- 22. Solution: 1 1 0 0 1 2 3 0 ( ) ( ) 6 (1 ) 6 2 3 1 i f x dx x x dx x x Dr. S. Kalyani PRP 22
- 23. 1 2 1 3 2 3 1 3 ( ) 1 1 ( ) 1 1 2 3 2 ( | ) 1 2 2 3 3 ( ) 3 3 6 (1 ) = 6 (1 ) 11 11 54 13 26 27 ii P X P X X P X x x dx x x dx Dr. S. Kalyani PRP 23
- 24. 1 0 2 3 2 3 3 2 ( ) ( ) ( ) 6 (1 ) 6 (1 ) 3 2 3(1 ) 2(1 ) 4 6 1 0 1 1 3 , 2 2 1 The only possible value of k in the given range is . 2 1 2 k k iii We have P X k P X k x x dx x x dx k k k k k k k k Dr. S. Kalyani PRP 24
- 25. Dr. S. Kalyani PRP 25 𝑖𝑣) 𝐹 𝑥 = −∞ 𝑥 𝑓 𝑥 𝑑𝑥 𝐹 𝑥 = 0 𝑥 6𝑥 1 − 𝑥 𝑑𝑥 = 0 𝑥 (6𝑥 − 6𝑥2 )𝑑𝑥 = 6 𝑥2 2 − 6 𝑥3 3 0 𝑥 𝐹(𝑥) = 3𝑥2 − 2𝑥3 is the cumulative distribution function
- 26. Dr. S. Kalyani PRP 26 Problem The distribution function of a random variable X is given by 𝐹 𝑋 = 1 − 1 + 𝑥 𝑒−𝑥 , 𝑥 ≥ 0 Find the density function. Solution: We know that 𝑓 𝑥 = 𝑑 𝑑𝑥 𝐹 𝑥 = 𝑑 𝑑𝑥 {1 − 𝑒−𝑥 − 𝑥𝑒−𝑥} = 0 − −𝑒−𝑥 − (−𝑥𝑒−𝑥 + 𝑒−𝑥 ) = 𝑒−𝑥 + 𝑥𝑒−𝑥 − 𝑒−𝑥 = 𝑥𝑒−𝑥, 𝑥 ≥ 0. is the density function











![7
3
( ) (1.5 4.5 / 2)
( )
( / )
( )
[(1.5 4.5) ( 2)]
(1.5 4.5 / 2)
( 2)
( 3) ( 4)
( )
5
5
10
=
7 7
10
r
ii P X x
P A B
P A B
P B
P X X
P X X
P X
P X P X
P X r
Dr. S. Kalyani PRP 12
0 1 2 3 4 5](https://image.slidesharecdn.com/randomvariables-230531181413-dd80f608/85/Random-variables-pptx-12-320.jpg)

![PROBLEM 3
A random Variable X has the following probability distribution.
Find
(i) the value of k
(ii) Evaluate P[X<2] and P[-2<X<2]
(iii)Find the cumulative Distribution of X.
x -2 -1 0 1 2 3
p(x) 0.1 k 0.2 2k 0.3 3k
Dr. S. Kalyani PRP 14](https://image.slidesharecdn.com/randomvariables-230531181413-dd80f608/85/Random-variables-pptx-14-320.jpg)
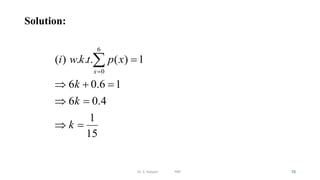

![Dr. S. Kalyani PRP 17
( )
[ ]
[ ] [ ] [ ]
2 2
1 0 1
1 2
0.2
15 15
3
= 0.2
15
2
5
ii
P X
P X P X P X
- < <
= = - + = + =
= + +
+
=](https://image.slidesharecdn.com/randomvariables-230531181413-dd80f608/85/Random-variables-pptx-17-320.jpg)








