regression analysis presentation slides.
- 1. Regression Analysis • Regression analysis is used in statistics to find trends in data. For example, you might guess that there’s a connection between how much you eat and how much you weigh. • In statistical modelling, regression analysis is a set of statistical procedures for estimating the relationships between a dependent variable(outcome: weight) and one or more independent variable(predictors, covariates, features: amount of food we eat). • It provides an equation for a graph so that you can make predictions about your data.
- 2. Regression Analysis Example Year vs RainFall Record Formula can be represented as y=mx+b
- 3. Regression gives you a useful equation, which for this chart is: y = -2.2923x + 4624.4 • Best of all, you can use the equation to make predictions. For example, how much snow will fall in 2017? y = -2.2923(2017) + 4624.4 = 0.8 inches. • Regression also gives you an R2 value, which for this graph is 0.702. This number tells you how good your model is. • The values range from 0 to 1, with 0 being a terrible model and 1 being a perfect model. As you can probably see, 0.7 is a fairly decent model so you can be fairly confident in your weather prediction!
- 4. There are multiple benefits of using regression analysis: • It indicates the significant relationships between dependent variable and independent variable. • It indicates the strength of impact of multiple independent variables on a dependent variable. In Regression analysis, we fit a curve / line to the data points, in such a manner that the differences between the distances of data points from the curve or line is minimized. Regression Analysis
- 5. These techniques are mostly driven by three metrics (number of independent variables, type of dependent variables and shape of regression line). Regression Techniques
- 6. •Simple Linear regression(Univariate) analysis uses a single x variable for each dependent “y” variable. For example: (x, Y). •Multiple Linear regression(Multivariate) uses multiple “x” variables for each independent variable: (x1)1, (x2)1, (x3)1, Y1). •Nonlinear Regression if the regression curve is nonlinear then there is nonlinear regression between variables Regression Techniques
- 7. Regression Types 1.Simple and Multiple Linear Regression 2.Logistic Regression 3.Polynomial Regression 4.Ridge Regression and Lasso Regression (upgrades to Linear Regression)
- 8. Linear Regression • Dependent variable is continuous • Independent variable(s) can be continuous or discrete • Nature of regression line is linear. • It establishes a relationship between dependent variable (Y) and one or more independent variables (X) using a best fit straight line (also known as regression line). • Equation Y=m*X + c + e, where ‘c’ is intercept, ‘m’ is slope of the line and ’e’ is error term.
- 9. How to obtain best fit line (Value of m and c)? • Least Square Method: A most common method used for fitting a regression line. • It calculates the best-fit line for the observed data by minimizing the sum of the squares of the vertical deviations from each data point to the line. • Error is the difference between the actual value and Predicted value and the goal is to reduce this difference.
- 10. How to obtain best fit line (Value of m and c)? • The vertical distance between the data point and the regression line is known as Error or Residual. • Each data point has one residual and the sum of all the differences is known as the Sum of Residuals/Errors.
- 11. How to obtain best fit line (Value of m and c)? Residual/Error = Actual values – Predicted Values Sum of Residuals/Errors = Sum(Actual- Predicted Values) Square of Sum of Residuals/Errors = (Sum(Actual- Predicted Values))2 Aim is to minimize this sum of square error term or Cost Fuction
- 12. Least Square Method / Ordinary Least Square (OLS): For equation: y = mx + b
- 13. Use the least square method to determine the equation of line of best fit for the data. Then plot the line.
- 15. Metrix(s) for Model Evaluation • Residual Sum of Squares (RSS). Sum of difference between each actual output and the predicted output. • Mean Square Error (MSE) is computed as RSS divided by the total number of data points. • Root Mean Squared Error (RMSE)
- 16. Metrix(s) for Model Evaluation • R-squared is the proportion of the variance in the dependent variable that is predicted from the independent variable. • It ranges from 0 to 1. • With linear regression, the coefficient of determination is equal to the square of the correlation between the x and y variables. • If R2 is equal to 0, then the dependent variable cannot be predicted from the independent variable. • If R2 is equal to 1, then the dependent variable can be predicted from the independent variable without any error.
- 17. Metrix(s) for Model Evaluation R-squared: Formula 1: Using correlation coefficient Formula 2: Using sum of squares. Square this value to get the coefficient of determination
- 18. Example: • Last year, five randomly selected students took a math aptitude test before they began their statistics course. The Statistics Department has three questions: • What linear regression equation best predicts statistics performance, based on math aptitude scores? • If a student made an 80 on the aptitude test, what grade would we expect her to make in statistics? • How well does the regression equation fit the data? x 95 85 80 70 60 y 85 95 70 65 70
- 19. What linear regression equation best predicts statistics performance, based on math aptitude scores? If a student made an 80 on the aptitude test, what grade would we expect her to make in statistics? How well does the regression equation fit the data?
- 21. What linear regression equation best predicts statistics performance, based on math aptitude scores? If a student made an 80 on the aptitude test, what grade would we expect her to make in statistics? How well does the regression equation fit the data?
- 22. What linear regression equation best predicts statistics performance, based on math aptitude scores? If a student made an 80 on the aptitude test, what grade would we expect her to make in statistics? How well does the regression equation fit the data? Calculate the Value of R2
- 23. Linear Regression: Assumptions • Linearity: the dependent variable Y should be linearly related to independent variables. • Normality: The X and Y variables should be normally distributed • Homoscedasticity: The variance of the error terms should be constant • Independence/No Multicollinearity: No correlation should be there between the independent variables. • The error terms should be normally distributed • No Autocorrelation: The error terms should be independent of each other.
- 24. Cost Function • The whole idea of the linear Regression is to find the best fit line, which has very low error (cost function). Properties of the Regression line: • 1. The line minimizes the sum of squared difference between the observed values(actual y-value) and the predicted value(ŷ value) • 2. The line passes through the mean of independent and dependent features.
- 25. Cost Function vs Loss Function • The loss function calculates the error per observation, whilst the cost function calculates the error over the whole dataset.
- 26. Linear Regression: Gradient Descent • Gradient descent is an optimization algorithm used to find the values of parameters (coefficients) of a function that minimizes a cost function (cost). • The idea is to start with random m and b values and then iteratively updating the values, reaching minimum cost. • Steps: 1. Initially, the values of m and b will be 0 and the learning rate(α) will be introduced to the function. The value of learning rate(α) is taken very small, something between 0.01 or 0.0001. The learning rate is a tuning parameter in an optimization algorithm that determines the step size at each iteration while moving toward a minimum of a cost function.
- 27. Linear Regression: Gradient Descent 2. Partial derivative is calculate for the cost function equation in terms of slope(m) and also derivatives are calculated with respect to the intercept(b) 3. After the derivatives are calculated, The slope(m) and intercept(b) are updated with the help of the following equation. m = m-α*derivative of m b = b-α*derivative of b 4. The process of updating the values of m and b continues until the cost function reaches the ideal value of 0 or close to 0.
- 28. Multiple Linear Regression • The main difference is the number of independent variables that they take as inputs. Simple linear regression just takes a single feature, while multiple linear regression takes multiple x values. • Another way is to use Normal Equation with multiple independent variables.
- 29. Multiple Linear Regression • The main difference is the number of independent variables that they take as inputs. Simple linear regression just takes a single feature, while multiple linear regression takes multiple x values. ŷ = b0 + b1x1 + b2x2 + … + bk-1xk-1 + bkxk Y = Xb b = (X'X)-1 X'Y
- 30. Multiple Linear Regression: Example Student Test score IQ Study hours 1 100 110 40 2 90 120 30 3 80 100 20 4 70 90 0 5 60 80 10
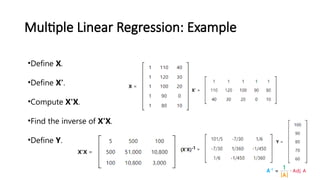
- 31. Multiple Linear Regression: Example •Define X. •Define X'. •Compute X'X. •Find the inverse of X'X. •Define Y.
- 32. Multiple Linear Regression: Example b = (X'X)-1 X'Y ŷ = 20 + 0.5x1 +0.5x2
- 33. Regression Types 1.Simple and Multiple Linear Regression 2.Logistic Regression 3.Polynomial Regression 4.Ridge Regression and Lasso Regression (upgrades to Linear Regression) 5.Decision Trees Regression 6.Support Vector Regression (SVR)
- 34. Logistic Regression • Logistic Regression is used when the dependent variable(target) is categorical or binary. For example: • To predict whether an email is spam (1) or (0) • Whether the tumor is malignant (1) or not (0) • Logistic regression is widely used for classification problems • Logistic regression doesn’t require linear relationship between dependent and independent variables. • Logistic regression estimates the probability of an event belonging to a class, such as voted or didn’t vote.
- 35. HR Analytics : IT firms recruit large number of people, but one of the problems they encounter is after accepting the job offer many candidates do not join. So, this results in cost over-runs because they have to repeat the entire process again. Now when you get an application, can you actually predict whether that applicant is likely to join the organization (Binary Outcome - Join / Not Join). Logistic Regression Example
- 36. Why Logistic Regression In Linear regression, we draw a straight line(the best fit line) L1 such that the sum of distances of all the data points to the line is minimal.
- 37. It uses sigmoid function is to map any predicted values of probabilities into another value between 0 and 1. Logistic Regression Equation Linear model: ŷ = b0+b1x Sigmoid function: σ(z) = 1/(1+e z − ) Logistic regression model: ŷ = σ(b0+b1x) = 1/(1+e-(b0+b1x) ) Also called logistic or logit function
- 38. Logistic Regression Equation To make in the range from 0 to +infinity To make in the range from -infinity to +infinity Since we want to calculate value of p
- 39. In logistic regression, as the output is a probability value between 0 or 1, mean squared error wouldn’t be the right choice. Instead, we use the log loss function which is derived from the maximum likelihood estimation method. Logistic Regression Evaluation
- 41. Bias • Bias is simply defined as the inability of the model because of that there is some difference or error occurring between the model’s predicted value and the actual value. These differences between actual or expected values and the predicted values are known as error or bias error or error due to bias. • Let Y be the true value of a parameter, and let Y^ be an estimator of Y based on a sample of data. Then, the bias of the estimator Y^ is given by: • Bias(Y^)=E(Y^)–Y • where E(Y^) is the expected value of the estimator Y. It is the measurement of the model that how well it fits the data.
- 42. Bias • Low Bias: Low bias value means fewer assumptions are taken to build the target function. In this case, the model will closely match the training dataset. • High Bias: High bias value means more assumptions are taken to build the target function. In this case, the model will not match the training dataset closely. • The high-bias model will not be able to capture the dataset trend. It is considered as the underfitting model which has a high error rate. It is due to a very simplified algorithm.
- 43. Variance • The variance is the variability of the model that how much it is sensitive to another subset of the training dataset. i.e. how much it can adjust on the new subset of the training dataset. • Let Y be the actual values of the target variable, and Y^ be the predicted values of the target variable. • Then the variance of a model can be measured as the expected value of the square of the difference between predicted values and the expected value of the predicted values.
- 44. • Variance=E[(Y^–E[Y^])2] • where E[Yˉ]E[Yˉ] is the expected value of the predicted values. Here expected value is averaged over all the training data. • Variance errors are either low or high-variance errors. • Low variance: Low variance means that the model is less sensitive to changes in the training data and can produce consistent estimates of the target function with different subsets of data from the same distribution. This is the case of underfitting when the model fails to generalize on both training and test data. • High variance: High variance means that the model is very sensitive to changes in the training data and can result in significant changes in the estimate of the target function when trained on different subsets of data from the same distribution. This is the case of overfitting when the model performs well on the training data but poorly on new, unseen test data. It fits the training data too closely that it fails on the new training dataset.
- 45. Overfitting and Underfitting Underfitting is a situation when your model is too simple for your data or your hypothesis about data distribution is wrong and too simple. For example, your data is quadratic, and your model is linear. This situation is also called high bias. This means that your algorithm can do accurate predictions, but the initial assumption about the data is incorrect.
- 46. Overfitting and Underfitting Overfitting is a situation when your model is too complex for your data. For example, your data is linear and your model is high- degree polynomial. This situation is also called high variance. In this situation, changing the input data only a little, the model output changes very much. •low bias, low variance — is a good result, just right. •low bias, high variance — overfitting — the algorithm outputs very different predictions for similar data. •high bias, low variance — underfitting — the algorithm outputs similar predictions for similar data, but predictions are wrong (algorithm “miss”). •high bias, high variance — very bad algorithm. You will most likely never see this.
- 48. Regularization • Regularization is one of the ways to improve our model to work on unseen data by ignoring the less important features. • Regularization minimizes the validation loss and tries to improve the accuracy of the model. • It avoids overfitting by adding a penalty to the model with high variance.
- 49. LASSO stands for Least Absolute Shrinkage and Selection Operator. Lasso regression performs L1 regularization, i.e. it adds a factor of sum of absolute value of coefficients in the optimization objective. This type of regularization (L1) can lead to zero coefficients i.e. some of the features are completely neglected for the evaluation of output. So, Lasso regression not only helps in reducing over- Lasso Regression
- 50. In ridge regression, the cost function is altered by adding a penalty equivalent to square of the magnitude of the coefficients. The penalty term (lambda) regularizes the coefficients such that if the coefficients take large values the optimization function is penalized. Ridge regression shrinks the coefficients and it helps to reduce the model complexity and multi-collinearity It is also called “L2 regularization”. Ridge Regression
- 51. Polynomial Regression • A regression equation is a polynomial regression equation if the power of independent variable is more than 1. The equation below represents a polynomial equation: • In this regression technique, the best fit line is not a straight line. It is rather a curve that fits into the data points.
- 52. Lasso vs Ridge
- 53. Regression vs Classification • Classification predictions can be evaluated using accuracy, whereas regression predictions cannot. • Regression predictions can be evaluated using root mean squared error, whereas classification predictions cannot. • A classification algorithm may predict a continuous value, but the continuous value is in the form of a probability for a class label. • A regression algorithm may predict a discrete value, but the discrete value in the form of an integer quantity.










































![• Variance=E[(Y^–E[Y^])2]
• where E[Yˉ]E[Yˉ] is the expected value of the predicted values. Here expected value is
averaged over all the training data.
• Variance errors are either low or high-variance errors.
• Low variance: Low variance means that the model is less sensitive to changes in the
training data and can produce consistent estimates of the target function with
different subsets of data from the same distribution. This is the case of underfitting
when the model fails to generalize on both training and test data.
• High variance: High variance means that the model is very sensitive to changes in
the training data and can result in significant changes in the estimate of the target
function when trained on different subsets of data from the same distribution. This
is the case of overfitting when the model performs well on the training data but
poorly on new, unseen test data. It fits the training data too closely that it fails on the
new training dataset.](https://image.slidesharecdn.com/regressionanalysis-250102191738-82f59ae0/85/regression-analysis-presentation-slides-44-320.jpg)























































