Scaling Multinomial Logistic Regression via Hybrid Parallelism

Scaling Multinomial Logistic Regression via
Hybrid Parallelism
Parameswaran Raman
Ph.D. Candidate
University of California Santa Cruz
Tech Talk: Amazon
March 17 2020
1 / 62

Motivation
Data and Model grow hand in hand
2 / 62

e.g. Extreme Multi-class classiﬁcation
3 / 62

e.g. Extreme Multi-label classiﬁcation
http://manikvarma.org/downloads/XC/XMLRepository.html
4 / 62

e.g. Extreme Clustering
5 / 62

Challenges in Parameter Estimation
6 / 62

1 Storage limitations of Data and Model
6 / 62

2 Interdependence in parameter updates
6 / 62

3 Bulk-Synchronization is expensive
6 / 62

4 Synchronous communication is ineﬃcient
6 / 62

Traditional distributed machine learning approaches fall short.
6 / 62

Traditional distributed machine learning approaches fall short.
Hybrid-Parallel algorithms for parameter estimation!
6 / 62

Outline
1 Introduction
2 Distributed Parameter Estimation
3 Scaling Multinomial Logistic Regression [Raman et al., KDD 2019]
4 Conclusion and Future Directions
7 / 62

Regularized Risk Minimization
Goals in machine learning
8 / 62

We want to build a model using observed (training) data
8 / 62

Our model must generalize to unseen (test) data
8 / 62

min
θ
L (θ) = λ R (θ)
regularizer
+
1
N
N
i=1
loss (xi , yi , θ)
empirical risk
8 / 62

min
θ
L (θ) = λ R (θ)
regularizer
+
1
N
N
i=1
loss (xi , yi , θ)
empirical risk
X = {x1, . . . , xN}, y = {y1, . . . , yN} is the observed training data
θ are the model parameters
8 / 62

min
θ
L (θ) = λ R (θ)
regularizer
+
1
N
N
i=1
loss (xi , yi , θ)
empirical risk
loss (·) to quantify model’s performance
8 / 62

min
θ
L (θ) = λ R (θ)
regularizer
+
1
N
N
i=1
loss (xi , yi , θ)
empirical risk
loss (·) to quantify model’s performance
regularizer R (θ) to avoid over-ﬁtting (penalizes complex models)
8 / 62

Frequentist Models
Binary Classiﬁcation/Regression
Multinomial Logistic Regression
Matrix Factorization
Latent Collaborative Retrieval
Polynomial Regression, Factorization Machines
9 / 62

Bayesian Models
p(θ|X)
posterior
=
likelihood
p(X|θ) ·
prior
p(θ)
p(X, θ)dθ
marginal likelihood (model evidence)
prior plays the role of regularizer R (θ)
likelihood plays the role of empirical risk
10 / 62

Bayesian Models
Gaussian Mixture
Models (GMM)
Latent Dirichlet
Allocation (LDA)
p(θ|X)
posterior
=
likelihood
p(X|θ) ·
prior
p(θ)
p(X, θ)dθ
marginal likelihood (model evidence)
prior plays the role of regularizer R (θ)
likelihood plays the role of empirical risk
10 / 62

Focus on Matrix Parameterized Models
N
D
X
Data
D
K
θ
Model
11 / 62

Focus on Matrix Parameterized Models
N
D
X
Data
D
K
θ
Model
What if these matrices do not ﬁt in memory?
11 / 62

Outline
1 Introduction
12 / 62

Distributed Parameter Estimation
13 / 62

Data parallel
N
D
X
Data
D
K
θ
Model
e.g. L-BFGS
13 / 62

Data parallel
N
D
X
Data
D
K
θ
Model
e.g. L-BFGS
Model parallel
N
D
X
Data
D
K
θ
Model
e.g. LC [Gopal et al., 2013]
13 / 62

Good
Easy to implement using map-reduce
Scales as long as Data or Model ﬁts in memory
14 / 62

Good
Bad
Either Data or the Model is replicated on each worker.
14 / 62

Good
Bad
Data Parallel: Each worker requires O N×D
P + O (K × D)
bottleneck
14 / 62

Good
Bad
Data Parallel: Each worker requires O N×D
P + O (K × D)
bottleneck
Model Parallel: Each worker requires requires O (N × D)
bottleneck
+O K×D
P
14 / 62

Question
Can we get the best of both worlds?
15 / 62

Hybrid Parallelism
N
D
X
Data
D
K
θ
Model
16 / 62

Hybrid-Parallelism
1 One versatile method for all regimes of data and model parallelism
17 / 62

Why Hybrid Parallelism?
18 / 62

19 / 62

20 / 62

21 / 62

LSHTC1-small
LSHTC1-large
ODP
Youtube8M-Video
Reddit-Full
101
102
103
104
105
106
max memory of commodity machine
SizeinMB(log-scale)
data size (MB)
parameters size (MB)
22 / 62

Hybrid-Parallelism
2 Independent parameter updates on each worker
23 / 62

Hybrid-Parallelism
2 Independent parameter updates on each worker
3 Fully de-centralized and asynchronous optimization algorithms
24 / 62

How do we achieve Hybrid Parallelism in machine learning models?
25 / 62

Double-Separability
Hybrid Parallelism
26 / 62

Double-Separability
Deﬁnition
A function f in two sets of parameters θ and θ is doubly separable if it
can be decomposed into sub-functions fij such that:
f (θ1, θ2, . . . , θm, θ1, θ2, . . . , θm ) =
m
i=1
m
j=1
fij (θi , θj )
27 / 62

Double-Separability
f (θ1, θ2, . . . , θm, θ1, θ2, . . . , θm ) =
m
i=1
m
j=1
fij (θi , θj )
28 / 62

Double-Separability
f (θ1, θ2, . . . , θm, θ1, θ2, . . . , θm ) =
m
i=1
m
j=1
fij (θi , θj )
x
x
x
x
x
x
x
x
x
x
x
x x
m
m
fij (θi , θj )
28 / 62

Double-Separability
f (θ1, θ2, . . . , θm, θ1, θ2, . . . , θm ) =
m
i=1
m
j=1
fij (θi , θj )
x
x
x
x
x
x
x
x
x
x
x
x x
m
m
fij (θi , θj )
fij corresponding to
highlighted diagonal blocks
can be computed
independently and in
parallel
28 / 62

Direct Double-Separability
e.g. Matrix Factorization
29 / 62

L(w1, w2, . . . , wN, h1, h2, . . . , hM) =
1
2
N
i=1
M
j=1
(Xij − wi , hj )2
29 / 62

L(w1, w2, . . . , wN, h1, h2, . . . , hM) =
1
2
N
i=1
M
j=1
(Xij − wi , hj )2
Objective function is trivially doubly-separable! [Yun et al 2014]
29 / 62

Others require Reformulations
30 / 62

Doubly-Separable Multinomial Logistic Regression
(DS-MLR)
min
W
λ
2
K
k=1
wk
2
−
1
N
N
i=1
K
k=1
yikwT
k xi +
1
N
N
i=1
log
K
k=1
exp(wT
k xi )
makes model parallelism hard
Doubly-Separable form
min
W ,A
N
i=1
K
k=1
λ wk
2
2N
−
yik wT
k xi
N
−
log ai
NK
+
exp(wT
k xi + log ai )
N
−
1
NK
31 / 62

Outline
1 Introduction
32 / 62

Multinomial Logistic Regression (MLR)
Given:
Training data (xi , yi )i=1,...,N,
xi ∈ RD
Labels yi ∈ {1, 2, . . . , K}
N
D
X
Data
y
33 / 62

Given:
xi ∈ RD
Labels yi ∈ {1, 2, . . . , K}
N
D
X
Data
y
Goal:
Learn a model W
Predict labels for the test
data points using W
D
K
W
Model
33 / 62

Given:
xi ∈ RD
Labels yi ∈ {1, 2, . . . , K}
N
D
X
Data
y
Goal:
Learn a model W
Predict labels for the test
data points using W
D
K
W
Model
Assume: N, D and K are large (N >>> D >> K)
33 / 62

The probability that xi belongs to class k is given by:
p(yi = k|xi , W ) =
exp(wk
T xi )
K
j=1 exp(wj
T xi )
where W = {w1, w2, . . . , wK } denotes the parameter for the model.
34 / 62

The corresponding l2 regularized negative log-likelihood loss:
min
W
λ
2
K
k=1
wk
2
−
1
N
N
i=1
K
k=1
yikwk
T
xi +
1
N
N
i=1
log
K
k=1
exp(wk
T
xi )
where λ is the regularization hyper-parameter.
35 / 62

The corresponding l2 regularized negative log-likelihood loss:
min
W
λ
2
K
k=1
wk
2
−
1
N
N
i=1
K
k=1
yikwk
T
xi +
1
N
N
i=1
log
K
k=1
exp(wk
T
xi )
makes model parallelism hard
where λ is the regularization hyper-parameter.
36 / 62

Reformulation into Doubly-Separable form
Log-concavity bound [Bouchard07]
log(γ) ≤ a · γ − log(a) − 1, ∀γ, a > 0,
where a is a variational parameter. This bound is tight when a = 1
γ .
37 / 62

Reformulating the objective of MLR
min
W ,A
λ
2
K
k=1
wk
2
+
1
N
N
i=1
−
K
k=1
yik wk
T
xi + ai
K
k=1
exp(wk
T
xi ) − log(ai ) − 1
where ai can be computed in closed form as:
ai =
1
K
k=1 exp(wk
T xi )
38 / 62

(DS-MLR)
Doubly-Separable form
min
W ,A
N
i=1
K
k=1
λ wk
2
2N
−
yik wk
T
xi
N
−
log ai
NK
+
exp(wk
T
xi + log ai )
N
−
1
NK
39 / 62

(DS-MLR)
Stochastic Gradient Updates
Each term in stochastic update depends on only data point i and class k.
40 / 62

(DS-MLR)
wk
t+1 ← wk
t − ηtK λxi − yikxi + exp wk
T xi + log ai xi
40 / 62

(DS-MLR)
wk
t+1 ← wk
t − ηtK λxi − yikxi + exp wk
T xi + log ai xi
log ai
t+1 ← log ai
t − ηtK exp(wk
T xi + log ai ) − 1
K
40 / 62

Access Pattern of updates: Stoch wk, Stoch ai
X
W
A
(a) Updating wk only requires
computing ai
X
W
A
(b) Updating ai only requires
accessing wk and xi .
41 / 62

Updating ai: Closed form instead of Stoch update
Closed-form update for ai
ai =
1
K
k=1 exp(wk
T xi )
42 / 62

Access Pattern of updates: Stoch wk, Exact ai
X
W
A
(a) Updating wk only requires
computing ai
X
W
A
(b) Updating ai requires accessing
entire W. Synchronization
bottleneck!
43 / 62

Updating ai: Avoiding bulk-synchronization
ai =
1
K
k=1 exp(wk
T xi )
44 / 62

ai =
1
K
k=1 exp(wk
T xi )
Each worker computes partial sum using the wk it owns.
44 / 62

ai =
1
K
k=1 exp(wk
T xi )
Each worker computes partial sum using the wk it owns.
P workers: After P rounds the global sum is available
44 / 62

Parallelization: Synchronous DSGD [Gemulla et al., 2011]
X and local parameters A are partitioned horizontally (1, . . . , N)
45 / 62

Global model parameters W are partitioned vertically (1, . . . , K)
45 / 62

Global model parameters W are partitioned vertically (1, . . . , K)
P = 4 workers work on mutually-exclusive blocks of A and W
45 / 62

Parallelization: Asynchronous NOMAD [Yun et al., 2014]
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
xx
x
x
xx
A
W
46 / 62

Parallelization: Asynchronous NOMAD [Yun et al 2014]
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
xx
x
x
xx
A
W
47 / 62

x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
xx
x
x
xx
A
W
48 / 62

x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
xx
x
x
xx
A
W
49 / 62

Experiments: Single Machine
NEWS20, Data=35 MB, Model=9.79 MB
100 101 102 103
1.45
1.5
1.55
1.6
1.65
time (secs)
objective
DS-MLR
L-BFGS
LC
51 / 62

Experiments: Single Machine
LSHTC1-small, Data=15 MB, Model=465 MB
101 102 103 104
0
0.2
0.4
0.6
0.8
1
time (secs)
objective
DS-MLR
L-BFGS
LC
52 / 62

Experiments: Multi Machine
LSHTC1-large, Data=356 MB, Model=34 GB,
machines=4, threads=12
103 104
0.5
0.6
0.7
0.8
time (secs)
objective
DS-MLR
LC
53 / 62

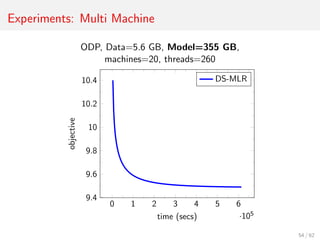
Experiments: Multi Machine
ODP, Data=5.6 GB, Model=355 GB,
0 1 2 3 4 5 6
·105
9.4
9.6
9.8
10
10.2
10.4
time (secs)
objective
DS-MLR
54 / 62

Experiments: Multi Machine Dense Dataset
YouTube-Video, Data=76 GB, Model=43 MB,
0 1 2 3
·105
0
20
40
60
time (secs)
objective
DS-MLR
55 / 62

Experiments: Multi Machine (Nothing ﬁts in memory!)
Reddit-Full, Data=228 GB, Model=358 GB,
0 2 4 6
·105
10
10.2
10.4
time (secs)
objective DS-MLR
211 million examples, 44 billion parameters (# features × # classes)
56 / 62

Outline
1 Introduction
57 / 62

Conclusion and Key Takeaways
Data and Model grow hand in hand.
58 / 62

Challenges in Parameter Estimation.
58 / 62

I have developed:
58 / 62

I have developed:
Hybrid-Parallel formulations
58 / 62

I have developed:
Distributed, Asynchronous Algorithms
58 / 62

I have developed:
Distributed, Asynchronous Algorithms
Applied them to several machine learning tasks:
Classiﬁcation (e.g. Multinomial Logistic Regression)
Clustering (e.g. Mixture Models)
Ranking
58 / 62

Summary: Other Hybrid-Parallel formulations
59 / 62

Ongoing Work: Other Matrix Parameterized Models
60 / 62

Factorization Machines
60 / 62

Inﬁnite Mixture Models
60 / 62

DP Mixture Model [BleiJordan2006]
60 / 62

Pittman-Yor Mixture Model [Dubey et al., 2014]
60 / 62

Stochastic Mixed-Membership Block Models [Airoldi et al., 2008]
60 / 62

Stochastic Mixed-Membership Block Models [Airoldi et al., 2008]
Deep Neural Networks [Wang et al., 2014]
60 / 62

Acknowledgements
Thanks to all my collaborators.
61 / 62

References
Parameswaran Raman, Sriram Srinivasan, Shin Matsushima, Xinhua
Zhang, Hyokun Yun, S.V.N. Vishwanathan. Scaling Multinomial Logistic
Regression via Hybrid Parallelism. KDD 2019.
Parameswaran Raman∗
, Jiong Zhang∗
, Shihao Ji, Hsiang-Fu Yu, S.V.N.
Vishwanathan, Inderjit S. Dhillon. Extreme Stochastic Variational Inference:
Distributed and Asynchronous. AISTATS 2019.
Hyokun Yun, Parameswaran Raman, S.V.N. Vishwanathan. Ranking via
Robust Binary Classiﬁcation. NIPS 2014.
Source Code:
DS-MLR: https://bitbucket.org/params/dsmlr
ESVI: https://bitbucket.org/params/dmixmodels
RoBiRank: https://bitbucket.org/d ijk stra/robirank
62 / 62

Scaling Multinomial Logistic Regression via Hybrid Parallelism

Recommended

More Related Content

What's hot (19)

Similar to Scaling Multinomial Logistic Regression via Hybrid Parallelism (20)

Recently uploaded (20)

Scaling Multinomial Logistic Regression via Hybrid Parallelism