Shortest path problem

Jun 16, 2014Download as PPTX, PDF8 likes9,998 views

This document presents information about the shortest path problem in graphs. It defines key graph terms like vertices, edges, and discusses weighted, directed, and undirected graphs. It provides an example of finding the shortest path between two vertices in a graph using Dijkstra's algorithm and walks through the steps of running the algorithm on a sample graph to find the shortest path between vertices 1 and 9.

PRESENTED TO:
MAM MERYAM
DEPARTMENT OF
COMPUTER SCIENCE

GROUP MEMBERS:
IFRA ILYAS (470)
AQSA SHAUKAT (586)
PAZEER ZARA (452)
SAMRA ASLAM (427)
AQSA ANWAR (453)

GRAPH:
 A graph is a representation of a set of objects
where some pairs of objects are connected by links.
 Vertices:
The interconnected objects are represented
by mathematical abstractions called vertices.
 Edges:
The links that connect some pairs of vertices
are called edges.

SHORTEST PATH
PROBLEM :
 The shortest path problem is the problem of finding
a path between two vertices in a graph such that
the sum of the weights of its constituent edges is
minimized.


TYPES OF GRAPH:
1. Weighted graph
2. Un-weighted graph
3. Directed graph
4. Un-directed graph

TYPES OF GRAPHS:
 Weighted:
A graph is a
weighted graph if a
number (weight) is
assigned to each edge.
Example:
Such weights might
represent, for example,
costs, lengths or
capacities, etc.
 Un-weighted:
A graph is a un-
weighted graph if a
number(weight) is not
assigned to each edge.

TYPES OF GRAPHS:
 Directed:
An directed
graph is one in which
edges have orientation.
 Un-directed:
An undirected
graph is one in which
edges have no
orientation.

SHORTEST PATH PROBLEM:
 Given the graph below, suppose we wish to
find the shortest path from vertex 1 to vertex
13.

EXAMPLE:
 After some consideration, we may determine
that the shortest path is as follows, with length
14
 Other paths exists, but they are longer

NEGATIVE CYCLES:
 Clearly, if we have negative vertices, it may be
possible to end up in a cycle whereby each pass
through the cycle decreases the total length
 Thus, a shortest length would be undefined for such
a graph
 Consider the shortest path
from vertex 1 to 4...
 We will only consider non-
negative weights.

SHORTEST PATH EXAMPLE:
 Given:
 Weighted Directed graph G = (V, E).
 Source s, destination t.
 Find shortest directed path from s to t.
s
3
t
2
6
7
4
5
23
18
2
9
14
15
5
30
20
44
16
11
6
19
6
Cost of path s-2-3-5-t
= 9 + 23 + 2 + 16
= 48.

DISCUSSION ITEMS
 How many possible paths are there from s
to t?
 Can we safely ignore cycles? If so, how?
 Any suggestions on how to reduce the set of
possibilities?
s
3
t
2
6
7
4
5
23
18
2
9
14
15
5
30
20
44
16
11
6
19
6

KEY OBSERVATION:
 A key observation is that if the shortest path contains
the node v, then:
 It will only contain v once, as any cycles will only add to the
length.
 The path from s to v must be the shortest path to v from s.
 The path from v to t must be the shortest path to t from v.

DIJKSTRA’S ALGORITHM:
 Works when all of the weights are positive.
 Provides the shortest paths from a source to
all other vertices in the graph.
 Can be terminated early once the shortest
path to t is found if desired.

EXAMPLE:
 Consider the graph:
 the distances are appropriately initialized
 all vertices are marked as being unvisited

EXAMPLE:
 Visit vertex 1 and update its neighbours,
marking it as visited
 the shortest paths to 2, 4, and 5 are
updated

EXAMPLE:
 The next vertex we visit is vertex 4
 vertex 5 1 + 11 ≥ 8 don’t update
 vertex 7 1 + 9 < ∞ update
 vertex 8 1 + 8 < ∞ update

EXAMPLE:
 Next, visit vertex 2
 vertex 3 4 + 1 < ∞ update
 vertex 4 already
visited
 vertex 5 4 + 6 ≥ 8 don’t update
 vertex 6 4 + 1 < ∞ update

EXAMPLE:
 Next, we have a choice of either 3 or 6
 We will choose to visit 3
 vertex 5 5 + 2 < 8 update
 vertex 6 5 + 5 ≥ 5 don’t update

EXAMPLE:
 We then visit 6
 vertex 8 5 + 7 ≥ 9 don’t update
 vertex 9 5 + 8 < ∞ update

EXAMPLE:
 Next, we finally visit vertex 5:
 vertices 4 and 6 have already been visited
 vertex 7 7 + 1 < 10 update
 vertex 8 7 + 1 < 9 update
 vertex 9 7 + 8 ≥ 13 don’t update

EXAMPLE:
 Given a choice between vertices 7 and 8, we
choose vertex 7
 vertices 5 has already been visited
 vertex 8 8 + 2 ≥ 8 don’t update

EXAMPLE:
 Next, we visit vertex 8:
 vertex 9 8 + 3 < 13 update

EXAMPLE:
 Finally, we visit the end vertex
 Therefore, the shortest path from 1 to 9 has length
11

EXAMPLE:
 We can find the shortest path by working back from
the final vertex:
 9, 8, 5, 3, 2, 1
 Thus, the shortest path is (1, 2, 3, 5, 8, 9)

The document discusses several shortest path algorithms for graphs, including Dijkstra's algorithm, Bellman-Ford algorithm, and Floyd-Warshall algorithm. Dijkstra's algorithm finds the shortest path from a single source node to all other nodes in a graph with non-negative edge weights. Bellman-Ford can handle graphs with negative edge weights but is slower. Floyd-Warshall can find shortest paths in a graph between all pairs of nodes.

Classification and Characteristics of a serviceSanchit

The document discusses the key characteristics and classifications of services. It identifies 8 main characteristics of services: intangibility, perishability, inseparability, heterogeneity, ownership, simultaneity, quality measurement, and nature of demand. Services are also classified in several ways, including based on customer involvement (people processing, possession processing, mental stimulus processing, information processing). They can also be classified based on tangibility, whether linked to tangible goods or not. Services are further classified based on business orientation, skill/expertise requirements, and end user (consumer, business-to-business, industrial).

Land Resources and Associated Problemsjebinjohn42

Land is a natural resource essential for humanity and ecosystems. It provides agricultural resources and minerals. Land degradation occurs through deforestation, overgrazing, and unsustainable agricultural practices like excessive fertilizer and pesticide use. This pollutes soil and water resources and degrades land quality. Landslides can be natural or human-induced by irresponsible construction, mining, and road building. Soil erosion is the wearing away of topsoil by water and wind forces. It reduces crop productivity and pollutes waterways. Desertification is the process of fertile land turning into desert due to climate change and human activities like overgrazing, unsustainable farming, and urbanization. Prevention methods include sustainable land management policies, education, and technology

ppt on pavement designRohit Ranjan

The document discusses different types of pavements. It describes flexible pavements as having multiple layers that distribute loads through aggregate interlock. Rigid pavements distribute loads through the beam strength of concrete slabs. Flexible pavements are composed of surface, base, and sub-base layers over a subgrade, while rigid pavements typically only require a concrete surface layer. Both pavement types are designed to reduce loads from vehicles to prevent damage to the subgrade. The document compares advantages and disadvantages of flexible and rigid pavements.

File Management in Operating SystemJanki Shah

Lecture 6- Deadlocks.pptxAmanuelmergia

The document discusses deadlocks in operating systems. It defines deadlock and describes the four conditions required for deadlock: mutual exclusion, hold and wait, no preemption, and circular wait. Methods for handling deadlocks include prevention, avoidance, detection, and recovery. Prevention ensures at least one deadlock condition does not occur. Avoidance uses a resource allocation graph and banker's algorithm to ensure the system never enters an unsafe state. Detection finds deadlocks and recovery releases processes to break deadlocks.

Types of maintenanceAbhik Rathod

This document discusses different types of maintenance for assets including aircraft. It defines maintenance as work carried out to preserve assets and enable continued use over their design life. The main types of maintenance discussed are: breakdown, preventive (periodic and predictive), and corrective. Periodic maintenance involves regular inspection and servicing, while predictive uses condition monitoring. Aircraft maintenance checks ranging from light A/B checks every 500-800 hours to comprehensive D checks every 5 years are also outlined. Nondestructive testing methods like liquid penetrant and eddy current are used during aircraft maintenance inspections.

Firewall and its types and functionNisarg Amin

This document discusses firewalls and their types and functions. It defines a firewall as a system used to control access between trusted and untrusted networks using pre-configured rules. There are two main types of firewalls - hardware firewalls which are physical devices that protect entire networks, and software firewalls which are applications installed on individual computers. The document also outlines several firewall techniques including packet filtering, application gateways, circuit-level gateways, and bastion hosts. It provides examples of what personal firewalls can and cannot do to protect individual computers.

Dijkstrajagdeeparora86

This document provides an overview of representing graphs and Dijkstra's algorithm in Prolog. It discusses different ways to represent graphs in Prolog, including using edge clauses, a graph term, and an adjacency list. It then explains Dijkstra's algorithm for finding the shortest path between nodes in a graph and provides pseudocode for implementing it in Prolog using rules for operations like finding the minimum value and merging lists.

Dijkstra s algorithmmansab MIRZA

Floyd warshall algorithmA. S. M. Shafi

The Floyd-Warshall algorithm finds the shortest paths between all pairs of vertices in a weighted graph. It can handle both directed and undirected graphs, except those with negative cycles. The algorithm works by iteratively updating a distance matrix to track the shortest distances between all pairs as it considers paths that pass through intermediate vertices. It runs in O(n3) time, where n is the number of vertices.

Floyd Warshall AlgorithmInteX Research Lab

This document presents an overview of the Floyd-Warshall algorithm. It begins with an introduction to the algorithm, explaining that it finds shortest paths in a weighted graph with positive or negative edge weights. It then discusses the history and naming of the algorithm, attributed to researchers in the 1950s and 1960s. The document proceeds to provide an example of how the algorithm works, showing the distance and sequence tables that are updated over multiple iterations to find shortest paths between all pairs of vertices. It concludes with discussing the time and space complexity, applications, and references.

Dijkstra's algorithmgsp1294

Dijkstra's algorithm finds the shortest paths from a source node to all other nodes in a graph. It works by maintaining two sets - one for nodes whose shortest paths are determined, and one for remaining nodes. It iteratively selects the node with the smallest distance from the source, calculates the distances to its neighbors, and moves them to the determined set until all nodes are processed. Some applications include finding fastest routes in transportation networks like road maps or flight schedules.

Dijkstra’S Algorithmami_01

Dijkstra's algorithm is a graph search algorithm that finds the shortest paths between nodes in a graph. It was developed by computer scientist Edsger Dijkstra in 1956. The algorithm works by assigning tentative distances to nodes in the graph and updating them until it determines the shortest path from the starting node to all other nodes. It can be used to find optimal routes between locations on a map by treating locations as nodes and distances between them as edge costs. ArcGIS Network Analysis software uses Dijkstra's algorithm to solve network problems like finding the lowest cost route, service areas, and closest facilities.

Minimum spanning treeHinal Lunagariya

The document discusses minimum spanning tree algorithms for finding low-cost connections between nodes in a graph. It describes Kruskal's algorithm and Prim's algorithm, both greedy approaches. Kruskal's algorithm works by sorting edges by weight and sequentially adding edges that do not create cycles. Prim's algorithm starts from one node and sequentially connects the closest available node. Both algorithms run in O(ElogV) time, where E is the number of edges and V is the number of vertices. The document provides examples to illustrate the application of the algorithms.

Dijkstra’s algorithmfaisal2204

The document describes Dijkstra's algorithm for finding the shortest paths between nodes in a graph. It begins with an overview of how the algorithm works by solving subproblems to find the shortest path from the source to increasingly more nodes. It then provides pseudocode for the algorithm and analyzes its time complexity of O(E+V log V) when using a Fibonacci heap. Some applications of the algorithm include traffic information systems and routing protocols like OSPF.

Shortest Path in GraphDr Sandeep Kumar Poonia

The document discusses algorithms for finding shortest paths in graphs. It describes Dijkstra's algorithm and Bellman-Ford algorithm for solving the single-source shortest paths problem and Floyd-Warshall algorithm for solving the all-pairs shortest paths problem. Dijkstra's algorithm uses a priority queue to efficiently find shortest paths from a single source node to all others, assuming non-negative edge weights. Bellman-Ford handles graphs with negative edge weights but is slower. Floyd-Warshall finds shortest paths between all pairs of nodes in a graph.

SINGLE-SOURCE SHORTEST PATHS Md. Shafiuzzaman Hira

The document discusses different single-source shortest path algorithms. It begins by defining shortest path and different variants of shortest path problems. It then describes Dijkstra's algorithm and Bellman-Ford algorithm for solving the single-source shortest paths problem, even in graphs with negative edge weights. Dijkstra's algorithm uses relaxation and a priority queue to efficiently solve the problem in graphs with non-negative edge weights. Bellman-Ford can handle graphs with negative edge weights but requires multiple relaxation passes to converge. Pseudocode and examples are provided to illustrate the algorithms.

Spanning trees & applicationsTech_MX

This document discusses minimum spanning trees. It defines a minimum spanning tree as a spanning tree of a connected, undirected graph that has a minimum total cost among all spanning trees of that graph. The document provides properties of minimum spanning trees, including that they are acyclic, connect all vertices, and have n-1 edges for a graph with n vertices. Applications of minimum spanning trees mentioned include communication networks, power grids, and laying telephone wires to minimize total length.

Dijkstra's Algorithm Rashik Ishrak Nahian

Prim's algorithmPankaj Thakur

Dijkstra's algorithm presentationSubid Biswas

Traveling salesman problemJayesh Chauhan

The document describes the traveling salesman problem (TSP) and how to solve it using a branch and bound approach. The TSP aims to find the shortest route for a salesman to visit each city once and return to the starting city. It can be represented as a weighted graph. The branch and bound method involves reducing the cost matrix by subtracting minimum row/column values, building a state space tree of paths, and choosing the path with the lowest cost at each step. An example demonstrates these steps to find the optimal solution of 24 for a 5 city TSP problem.

SINGLE SOURCE SHORTEST PATH.pptshanthishyam

This document discusses several algorithms for finding single-source shortest paths in graphs: 1) Bellman-Ford algorithm can handle graphs with negative edge weights by detecting negative cycles. It runs in O(VE) time. 2) For directed acyclic graphs (DAGs), topological sorting followed by relaxation yields the shortest paths from a single source in O(V+E) time. 3) Dijkstra's algorithm uses a greedy approach to find single-source shortest paths in graphs with non-negative edge weights.

Graph colouringPriyank Jain

This document discusses graph coloring, which involves assigning colors to the vertices of a graph such that no two adjacent vertices have the same color. It provides examples of problems that can be modeled as graph coloring, such as scheduling committee meetings. The key points covered include defining graph coloring and chromatic number, discussing greedy algorithms and their limitations for graph coloring, and presenting the Welsh-Powell algorithm as an approach to graph coloring.

PRIM’S AND KRUSKAL’S ALGORITHMJaydeepDesai10

Prim's and Kruskal's algorithms are greedy algorithms used to find minimum spanning trees in graphs. Prim's algorithm builds the spanning tree by repeatedly adding the shortest edge that connects to the current tree. Kruskal's algorithm builds the tree by repeatedly adding the shortest edge that does not create a cycle. Both algorithms are used for applications like network design, cluster analysis, and map routing. The key difference is that Prim's starts from a node while Kruskal's starts from the minimum edge, making Prim's faster for dense graphs and Kruskal's faster for sparse graphs.

Graph Theory IntroductionMANISH T I

DAA-Floyd Warshall Algorithm.pptxArbabMaalik

The Floyd-Warshall algorithm finds the shortest paths between all pairs of vertices in a weighted graph. It works by computing the shortest path between every pair of vertices through dynamic programming. The algorithm proceeds in steps, where in each step it considers all vertices as potential intermediate vertices to find even shorter paths between vertex pairs. This is done by comparing the newly computed shortest paths to the values stored in the previous matrix.

Shortest path algorithmSubrata Kumer Paul

Dijkstra's algorithm is used to find the shortest paths from a source node to all other nodes in a network. It works by marking all nodes as tentative with initial distances from the source set to 0 and others to infinity. It then extracts the closest node, adds it to the shortest path tree, and relaxes distances of its neighbors. This process repeats until all nodes are processed. When applied to the example network, Dijkstra's algorithm finds the shortest path from node A to all others to be A-B=4, A-C=6, A-D=8, A-E=7, A-F=7, A-G=7, and A-H=9.

All pairs shortest path algorithmSrikrishnan Suresh

This document describes Floyd's algorithm for solving the all-pairs shortest path problem in graphs. It begins with an introduction and problem statement. It then describes Dijkstra's algorithm as a greedy method for finding single-source shortest paths. It discusses graph representations and traversal methods. Finally, it provides pseudocode and analysis for Floyd's dynamic programming algorithm, which finds shortest paths between all pairs of vertices in O(n3) time.

More Related Content

What's hot (20)

Dijkstrajagdeeparora86

Dijkstra s algorithmmansab MIRZA

Floyd warshall algorithmA. S. M. Shafi

Floyd Warshall AlgorithmInteX Research Lab

Dijkstra's algorithmgsp1294

Dijkstra’S Algorithmami_01

Minimum spanning treeHinal Lunagariya

Dijkstra’s algorithmfaisal2204

Shortest Path in GraphDr Sandeep Kumar Poonia

SINGLE-SOURCE SHORTEST PATHS Md. Shafiuzzaman Hira

Spanning trees & applicationsTech_MX

Dijkstra's Algorithm Rashik Ishrak Nahian

Prim's algorithmPankaj Thakur

Dijkstra's algorithm presentationSubid Biswas

Traveling salesman problemJayesh Chauhan

SINGLE SOURCE SHORTEST PATH.pptshanthishyam

Graph colouringPriyank Jain

PRIM’S AND KRUSKAL’S ALGORITHMJaydeepDesai10

Graph Theory IntroductionMANISH T I

DAA-Floyd Warshall Algorithm.pptxArbabMaalik

Dijkstrajagdeeparora86

Dijkstra s algorithmmansab MIRZA

Floyd warshall algorithmA. S. M. Shafi

Floyd Warshall AlgorithmInteX Research Lab

Dijkstra's algorithmgsp1294

Dijkstra’S Algorithmami_01

Minimum spanning treeHinal Lunagariya

Dijkstra’s algorithmfaisal2204

Shortest Path in GraphDr Sandeep Kumar Poonia

SINGLE-SOURCE SHORTEST PATHS Md. Shafiuzzaman Hira

Spanning trees & applicationsTech_MX

Dijkstra's Algorithm Rashik Ishrak Nahian

Prim's algorithmPankaj Thakur

Dijkstra's algorithm presentationSubid Biswas

Traveling salesman problemJayesh Chauhan

SINGLE SOURCE SHORTEST PATH.pptshanthishyam

Graph colouringPriyank Jain

PRIM’S AND KRUSKAL’S ALGORITHMJaydeepDesai10

Graph Theory IntroductionMANISH T I

DAA-Floyd Warshall Algorithm.pptxArbabMaalik

Viewers also liked (20)

Shortest path algorithmSubrata Kumer Paul

All pairs shortest path algorithmSrikrishnan Suresh

Conservation of codon optimalityAlistair Martin

Shortest path (Dijkistra's Algorithm) & Spanning Tree (Prim's Algorithm)Mohanlal Sukhadia University (MLSU)

The document discusses shortest path problems and algorithms for finding shortest paths in graphs. It describes Dijkstra's algorithm for finding the shortest path between two nodes in a graph with non-negative edge weights. Prim's algorithm is presented for finding a minimum spanning tree, which is a subgraph connecting all nodes with minimum total edge weight. An example graph is given and steps are outlined for applying Prim's algorithm to find its minimum spanning tree.

Dijkstra's Algorithmguest862df4e

Dijkstra's algorithm is a link-state routing algorithm that computes the least-cost paths from one node to all other nodes in a network. It works by iteratively building a set N' of nodes whose least-cost paths are known, starting from a source node. In each iteration, it finds the node w not in N' with the minimum path cost and updates the cost estimates to nodes adjacent to w. This process repeats until all nodes are in N', providing the shortest path forwarding table for the source node. The algorithm runs in O(n^2) time for n nodes but more efficient implementations exist. Oscillations can potentially occur if link costs change based on traffic loads.

Shortest Path ProblemGuillaume Guérard

The document discusses shortest path problems in graphs. It introduces the shortest path problem and describes algorithms for finding shortest paths from a single source (Dijkstra's and Bellman-Ford algorithms) and for all vertex pairs (Bellman-Ford algorithm). It also discusses dynamic programming, linear programming formulations, and properties like Bellman's principle of optimality and the existence of a shortest path tree from any starting vertex. Examples are provided to illustrate the algorithms.

Dijkstra algorithmare you

The document discusses finding the shortest route from Kota Bharu to Kuala Koh National Park in Kelantan, Malaysia using Dijkstra's parallel graph algorithm. The route passes through several places including Stong Mountain, Cintawasa Mountain, and Berangkat Mountain. Dijkstra's algorithm works by assigning infinite distances at first, then updating distances through visited neighbors until reaching the destination. The shortest path found is A to C to B to D to E, representing Kota Bharu to Stong Mountain to Cintawasa Mountain to Berangkat Mountain to Kuala Koh National Park.

My presentation all shortestpathCarlostheran

This document discusses algorithms for solving the all-pairs shortest path problem. It presents the Floyd-Warshall algorithm, which uses dynamic programming and matrix multiplication to solve this problem. The algorithm finds shortest paths between all pairs of vertices in a graph. It also describes Johnson's algorithm, which is more efficient for sparse graphs and uses Dijkstra's and Bellman-Ford algorithms as subroutines. It works by reweighting edges to eliminate negative cycles before running shortest path algorithms.

Shortest Path Search in Real Road Networks with pgRoutingDaniel Kastl

This document discusses pgRouting, an open source extension for PostgreSQL and PostGIS that provides routing functionality. It provides an overview of pgRouting, including the routing algorithms it supports like Dijkstra and A*, its data structure, demo sites, and the Web Routing Service which allows making pgRouting requests via HTTP. It also covers a demo of the Web Routing Service using OpenLayers and routing data from Japan and Canada.

Shortest path search for real road networks and dynamic costs with pgRoutingantonpa

This presentation will show the inside and current state of pgRouting development. It will explain the shortest path search in real road networks and how the data structure is important for getting better routing results. We will show how you can improve the quality of the search with dynamic costs and make the result look closer to the reality. We will demonstrate the way of using pgRouting together with other Open Source tools. Also you will learn about difficulties and limitations of implementing routing functionality in GIS applications, the difference between algorithms and their performance. pgRouting is an extension of PostgreSQL and PostGIS. A predecessor of pgRouting - pgDijkstra, written by Sylvain Pasche from Camptocamp, was extended by Orkney (Japan) and renamed to pgRouting, which now is a part of the PostLBS project. pgRouting can perform: * shortest path search (with 3 different algorithms) * Traveling Salesperson Problem solution (TSP) * driving distance geometry calculation

21 All Pairs Shortest PathAndres Mendez-Vazquez

As many things in the history of analysis of algorithms the all-pairs shortest path has a long history (From the point of view of Computer Science). We can see the initial results from the book “Studies in the Economics of Transportation” by Beckmann, McGuire, and Winsten (1956) where the notation that we use for the matrix multiplication alike was first used. In this slides, we go trough several all pairs Shortest path problem solutions from a slow version to the Johnson algorithm.

Biconnected components (13024116056)Akshay soni

This document discusses bi-connected components in graphs. It defines an articulation point as a vertex in a connected graph whose removal would disconnect the graph. A bi-connected component is a maximal subgraph that contains no articulation points. The document presents algorithms for identifying articulation points and bi-connected components in a graph using depth-first search (DFS). It introduces the concepts of tree edges, back edges, forward edges and cross edges in a DFS tree and explains how to use these edge types to determine if a vertex is an articulation point based on the minimum discovery time of its descendant vertices.

Unit26 shortest pathalgorithmmeisamstar

The document discusses the shortest path problem and Dijkstra's algorithm for solving it in graphs with non-negative edge weights. It defines the shortest path problem, explains that it is well-defined for non-negative graphs but not graphs with negative edge weights or cycles. It then describes Dijkstra's algorithm, how it works by iteratively finding the shortest path from the source to each vertex, and provides pseudocode for its implementation.

Avl treesMohd Arif

1) AVL trees are self-balancing binary search trees that maintain an O(log n) search time by ensuring the heights of the two child subtrees differ by at most 1 with rotations after insertions and deletions. 2) The balance factor of a node is defined as the height of its left subtree minus the height of its right subtree, and must be -1, 0, or 1 in an AVL tree. 3) There are four types of rotations (single, double) to rebalance the tree - right-right, left-left, left-right, and right-left - depending on the balance factor violated after an insertion or deletion.

AVL TreeChhatra Thapa

This document presents information about AVL trees through a slideshow presentation. It begins by defining AVL trees as binary search trees where the heights of the subtrees of any node differ by at most 1. It then discusses that AVL trees ensure searching, insertion, and deletion take O(log N) time by keeping the tree balanced through rotations. The presentation notes that AVL trees remain balanced through single and double rotations during insertions and deletions, and that rebalancing can be done in O(log N) time. It concludes by emphasizing that AVL trees guarantee O(log N) search time in dynamic environments through maintaining balance.

Solving The Shortest Path Tour ProblemNozir Shokirov

The Shortest Path Tour Problem is an extension to the normal Shortest Path Problem and appeared in the scientific literature in Bertsekas's dynamic programming and optimal control book in 2005, for the first time. This paper gives a description of the problem, two algorithms to solve it. Results to the numeric experimentation are given in terms of graphs. Finally, conclusion and discussions are made.

Floyd Warshall algorithm easy way to compute - MalingaMalinga Perera

The document demonstrates the Floyd-Warshall algorithm for finding the shortest paths between all pairs of vertices in a weighted graph. It shows the algorithm being applied to a sample graph with 4 vertices through a series of steps where the distances are updated. In each step, it considers all vertices as possible intermediates and updates the distances between vertex pairs accordingly until it reaches the shortest paths between all pairs of vertices in the graph.

The Shortest Route ProblemCharmaine Xy-Za Yape

The document discusses the shortest-route problem of finding the optimal path between a source and destination node in a network. It describes an algorithm to solve this problem by constructing a list of branches between nodes with their lengths, arranging them by ascending length, and then iteratively selecting the shortest remaining branch to determine the shortest route between the source and each subsequent node.

Minimum spanning TreeNarendra Singh Patel

Kruskal's algorithm finds a minimum spanning tree by growing it from a forest of trees. It works by repeatedly selecting the lowest cost edge that connects two different trees without forming a cycle and adding it to the spanning tree. This continues until only one tree remains, which is the minimum spanning tree. The algorithm considers edges in order of increasing weight, merging components with safe edges. It runs in O(ElogV) time by using a priority queue to track the lowest cost remaining edge.

Dynamic Programmingcontact2kazi

This document discusses dynamic programming techniques for solving optimization problems that can be divided into stages. It provides examples of using dynamic programming to find the shortest path from New York to Los Angeles, solve an inventory problem of determining optimal airplane production schedules, and allocate study time across courses to maximize grade points. Dynamic programming works by breaking problems into stages, finding optimal solutions for later stages, and then using these to recursively determine the optimal solutions for earlier stages working backwards.

Shortest path algorithmSubrata Kumer Paul

All pairs shortest path algorithmSrikrishnan Suresh

Conservation of codon optimalityAlistair Martin

Shortest path (Dijkistra's Algorithm) & Spanning Tree (Prim's Algorithm)Mohanlal Sukhadia University (MLSU)

Dijkstra's Algorithmguest862df4e

Shortest Path ProblemGuillaume Guérard

Dijkstra algorithmare you

My presentation all shortestpathCarlostheran

Shortest Path Search in Real Road Networks with pgRoutingDaniel Kastl

Shortest path search for real road networks and dynamic costs with pgRoutingantonpa

21 All Pairs Shortest PathAndres Mendez-Vazquez

Biconnected components (13024116056)Akshay soni

Unit26 shortest pathalgorithmmeisamstar

Avl treesMohd Arif

AVL TreeChhatra Thapa

Solving The Shortest Path Tour ProblemNozir Shokirov

Floyd Warshall algorithm easy way to compute - MalingaMalinga Perera

The Shortest Route ProblemCharmaine Xy-Za Yape

Minimum spanning TreeNarendra Singh Patel

Dynamic Programmingcontact2kazi

Similar to Shortest path problem (20)

01-05-2023, SOL_DU_MBAFT_6202_Dijkstra’s Algorithm Dated 1st May 23.pdfDKTaxation

Dijkstra's algorithm is used to find the shortest paths between nodes in a graph. It works by growing the shortest path tree one vertex at a time. It begins at the source node and examines all neighboring nodes, updating paths and tracking predecessors until the shortest path to every node has been determined. The Ford-Fulkerson method finds the maximum flow in a flow network by iteratively augmenting the flow along paths with available residual capacity until no more flow is possible. It works to push flow from the source to the sink along paths with available capacity until the network is saturated.

Unit ix graph Tribhuvan University

This document provides an overview of graphs and graph algorithms. It begins with an introduction to graphs, including definitions of vertices, edges, directed/undirected graphs, and graph representations using adjacency matrices and lists. It then covers graph traversal algorithms like depth-first search and breadth-first search. Minimum spanning trees and algorithms for finding them like Kruskal's algorithm are also discussed. The document provides examples and pseudocode for the algorithms. It analyzes the time complexity of the graph algorithms. Overall, the document provides a comprehensive introduction to fundamental graph concepts and algorithms.

Unit V - ppt.pptxKongunadu College of Engineering and Technology

Graphs are non-linear data structures used to represent connections between pairs of elements called nodes. Nodes represent real-world objects and edges represent the connections between nodes. Graphs can be used to model transportation networks, social networks, and more. There are different types of graphs including directed graphs, undirected graphs, weighted graphs, and more. Common graph algorithms include depth-first search, breadth-first search, topological sorting, minimum spanning trees, and more which have various applications.

Unit 9 graphDabbal Singh Mahara

Ds lec 5_chap4Self-Employed

This document discusses several graph theory concepts including: - A connected undirected graph contains a simple path between any two vertices. - Cut vertices and edges divide a graph into more components upon removal. - Euler circuits and paths visit every edge exactly once in a connected multigraph. - Planar graphs can be drawn in a plane without edge crossings. - Graph coloring assigns colors to vertices such that no adjacent vertices share a color.

logic.pptxKENNEDY GITHAIGA

DAA_Presentation - Copy.pptxAndrewJohnson866415

This document discusses algorithms for solving the all-pairs shortest path problem in graphs. It defines the all-pairs shortest path problem as finding the shortest path between every pair of nodes in a graph. It then describes two main algorithms for solving this problem: Floyd-Warshall and Johnson's algorithm. Floyd-Warshall finds all-pairs shortest paths in O(n3) time using dynamic programming. Johnson's algorithm improves this to O(V2logV+VE) time by first transforming the graph to make edges positive, then running Dijkstra's algorithm from each node.

Weighted graphsCore Condor

Graph dsuniversity of Gujrat, pakistan

This document discusses key concepts in graph theory and algorithms for finding paths in graphs: - It defines different types of graphs like simple graphs, directed graphs, and bipartite graphs. - It explains representations of graphs using adjacency matrices and lists. - It covers graph isomorphism, connected graphs, Euler paths and circuits, and Hamiltonian paths and cycles. - It introduces the shortest path problem and Dijkstra's algorithm for finding the shortest path between vertices in a weighted graph. - It provides an example applying Dijkstra's algorithm to find the shortest path between two vertices.

DATA STRUCTURES.pptxKENNEDY GITHAIGA

The document discusses graphs and graph algorithms. It begins by defining what a graph is - a collection of vertices connected by edges. It then lists four learning objectives related to representing graphs, traversing graphs, calculating minimum spanning trees, and finding shortest routes. The document goes on to describe different ways of representing graphs through adjacency matrices and lists. It also explains graph traversal algorithms like depth-first search and breadth-first search. Finally, it discusses algorithms for finding minimum spanning trees and shortest paths in weighted graphs.

UNIT III.pptxSwarndeviKm

Graphs are data structures used to represent connections between pairs of elements called nodes. The connections between nodes are called edges. There are different types of graphs such as weighted graphs where edges have a cost or value. Graphs can be represented using data structures like adjacency matrices and adjacency lists. Common graph algorithms include depth-first search (DFS), breadth-first search (BFS), minimum spanning trees (MST), shortest path algorithms like Dijkstra's algorithm, and topological sorting. Graphs have many real-world applications such as modeling transportation and social networks.

Data structure and algorithmsakthibalabalamuruga

This document discusses various algorithms for finding shortest paths in graphs, including Dijkstra's algorithm, breadth-first search (BFS), depth-first search (DFS), and Bellman-Ford algorithm. It provides pseudocode examples and explanations of how each algorithm works. It also covers properties of spanning trees, minimum spanning tree algorithms like Kruskal's and Prim's, and applications of spanning trees like network planning and routing protocols.

14 chapter9 graph_algorithmstopologicalsort_shortestpathSSE_AndyLi

1. The document defines various graph terms including vertices, edges, paths, cycles, connectivity, and graph representations. 2. It discusses topological sorting of directed acyclic graphs (DAGs) which finds an ordering of vertices such that if there is a path from v_i to v_j, then v_j appears after v_i. This can be done in O(|V|+|E|) time. 3. It also covers shortest path algorithms, including ones for unweighted graphs (BFS, O(|V|+|E|)), weighted graphs without negative edges (Dijkstra's algorithm, O(|E|log|V|)), and weighted graphs allowing negative

Graph_data_structure_information_engineering.pptxsahilpawar2426

A graph is a pictorial representation consisting of vertices connected by edges. It is represented as a pair of sets (V,E) where V is the set of vertices and E is the set of edges connecting vertex pairs. Key aspects include vertices, edges, adjacency, paths, degrees of vertices, directed/undirected graphs, cycles, and representations using adjacency matrices. Common graph algorithms are BFS, DFS, minimum spanning trees using Prim's and Kruskal's algorithms.

Dijkstra Shortest Path Algorithm in Network.pptRAJASEKARAN G

Dijkstra algorithm ds 57612334t4t44.pptssuser7b9bda1

Graphs and eularian circuit & path with c++ programMuhammad Danish Badar

This document discusses graphs and Eulerian paths and circuits. It begins by defining what a graph is - a set of nodes and edges. It then describes different types of graphs like directed/undirected, cyclic/acyclic, labeled, and weighted graphs. It explains the concepts of adjacency and connectivity in graphs. The document focuses on Eulerian paths and circuits, providing properties for a graph to have an Eulerian path or circuit. It presents pseudocode for an algorithm to check if a graph is Eulerian using depth-first search. Finally, it includes C++ code for a program that tests if input graphs exhibit an Eulerian path or circuit.

Graphs in Data Structurehafsa komal

The document discusses graphs and their applications. It defines graphs as consisting of vertices and edges. Graphs can be undirected or directed. It also defines concepts like paths, cycles, and connectivity in graphs. Common applications of graphs mentioned are maps, computer networks, and CAD designs. The document then discusses different ways to represent graphs using adjacency matrices and adjacency lists. It also discusses using graphs to model and solve problems like traffic light timing by coloring the vertices.

Algorithms of graphgetacew

Applied III Chapter 4(1).pdfDawitThomas

This document provides an overview of key concepts in vector calculus, including: - Vector calculus concepts such as limits, continuity, derivatives, and integrals of vector functions. - Operations on vectors like addition, subtraction, scalar multiplication. - Vector products including the dot product and cross product. - Applications of vector calculus like determining velocity, acceleration, and line, surface, and volume integrals. - Parametric representations of curves using a parameter like time, and their relation to geometry.

01-05-2023, SOL_DU_MBAFT_6202_Dijkstra’s Algorithm Dated 1st May 23.pdfDKTaxation

Unit ix graph Tribhuvan University

Unit V - ppt.pptxKongunadu College of Engineering and Technology

Unit 9 graphDabbal Singh Mahara

Ds lec 5_chap4Self-Employed

logic.pptxKENNEDY GITHAIGA

DAA_Presentation - Copy.pptxAndrewJohnson866415

Weighted graphsCore Condor

Graph dsuniversity of Gujrat, pakistan

DATA STRUCTURES.pptxKENNEDY GITHAIGA

UNIT III.pptxSwarndeviKm

Data structure and algorithmsakthibalabalamuruga

14 chapter9 graph_algorithmstopologicalsort_shortestpathSSE_AndyLi

Graph_data_structure_information_engineering.pptxsahilpawar2426

Dijkstra Shortest Path Algorithm in Network.pptRAJASEKARAN G

Dijkstra algorithm ds 57612334t4t44.pptssuser7b9bda1

Graphs and eularian circuit & path with c++ programMuhammad Danish Badar

Graphs in Data Structurehafsa komal

Algorithms of graphgetacew

Applied III Chapter 4(1).pdfDawitThomas

Recently uploaded (20)

new ppt artificial intelligence historyyyPianoPianist

Explainable-Artificial-Intelligence-XAI-A-Deep-Dive (1).pptxMahaveerVPandit

Artificial Intelligence (AI) basics.pptxaditichinar

Smart_Storage_Systems_Production_Engineering.pptxrushikeshnavghare94

five-year-soluhhhhhhhhhhhhhhhhhtions.pdfAdityaSharma944496

"Feed Water Heaters in Thermal Power Plants: Types, Working, and Efficiency G...Infopitaara

A feed water heater is a device used in power plants to preheat water before it enters the boiler. It plays a critical role in improving the overall efficiency of the power generation process, especially in thermal power plants. 🔧 Function of a Feed Water Heater: It uses steam extracted from the turbine to preheat the feed water. This reduces the fuel required to convert water into steam in the boiler. It supports Regenerative Rankine Cycle, increasing plant efficiency. 🔍 Types of Feed Water Heaters: Open Feed Water Heater (Direct Contact) Steam and water come into direct contact. Mixing occurs, and heat is transferred directly. Common in low-pressure stages. Closed Feed Water Heater (Surface Type) Steam and water are separated by tubes. Heat is transferred through tube walls. Common in high-pressure systems. ⚙️ Advantages: Improves thermal efficiency. Reduces fuel consumption. Lowers thermal stress on boiler components. Minimizes corrosion by removing dissolved gases.

QA/QC Manager (Quality management Expert)rccbatchplant

RICS Membership-(The Royal Institution of Chartered Surveyors).pdfMohamedAbdelkader115

railway wheels, descaling after reheating and before forgingJavad Kadkhodapour

Reagent dosing (Bredel) presentation.pptxAlejandroOdio

Lidar for Autonomous Driving, LiDAR Mapping for Driverless Cars.pptxRishavKumar530754

Raish Khanji GTU 8th sem Internship Report.pdfRaishKhanji

This report details the practical experiences gained during an internship at Indo German Tool Room, Ahmedabad. The internship provided hands-on training in various manufacturing technologies, encompassing both conventional and advanced techniques. Significant emphasis was placed on machining processes, including operation and fundamental understanding of lathe and milling machines. Furthermore, the internship incorporated modern welding technology, notably through the application of an Augmented Reality (AR) simulator, offering a safe and effective environment for skill development. Exposure to industrial automation was achieved through practical exercises in Programmable Logic Controllers (PLCs) using Siemens TIA software and direct operation of industrial robots utilizing teach pendants. The principles and practical aspects of Computer Numerical Control (CNC) technology were also explored. Complementing these manufacturing processes, the internship included extensive application of SolidWorks software for design and modeling tasks. This comprehensive practical training has provided a foundational understanding of key aspects of modern manufacturing and design, enhancing the technical proficiency and readiness for future engineering endeavors.

Mathematical foundation machine learning.pdfTalhaShahid49

Compiler Design_Lexical Analysis phase.pptxRushaliDeshmukh2

π0.5: a Vision-Language-Action Model with Open-World GeneralizationNABLAS株式会社

今回の資料「Transfusion / π0 / π0.5」は、画像・言語・アクションを統合するロボット基盤モデルについて紹介しています。拡散×自己回帰を融合したTransformerをベースに、π0.5ではオープンワールドでの推論・計画も可能に。 This presentation introduces robot foundation models that integrate vision, language, and action. Built on a Transformer combining diffusion and autoregression, π0.5 enables reasoning and planning in open-world settings.

Metal alkyne complexes.pptx in chemistrymee23nu

Introduction to Zoomlion Earthmoving.pptxAS1920

introduction to machine learining for beginersJoydebSheet

Smart Storage Solutions.pptx for production engineeringrushikeshnavghare94

some basics electrical and electronics knowledgenguyentrungdo88

new ppt artificial intelligence historyyyPianoPianist

Explainable-Artificial-Intelligence-XAI-A-Deep-Dive (1).pptxMahaveerVPandit

Artificial Intelligence (AI) basics.pptxaditichinar

Smart_Storage_Systems_Production_Engineering.pptxrushikeshnavghare94

five-year-soluhhhhhhhhhhhhhhhhhtions.pdfAdityaSharma944496

"Feed Water Heaters in Thermal Power Plants: Types, Working, and Efficiency G...Infopitaara

QA/QC Manager (Quality management Expert)rccbatchplant

RICS Membership-(The Royal Institution of Chartered Surveyors).pdfMohamedAbdelkader115

railway wheels, descaling after reheating and before forgingJavad Kadkhodapour

Reagent dosing (Bredel) presentation.pptxAlejandroOdio

Lidar for Autonomous Driving, LiDAR Mapping for Driverless Cars.pptxRishavKumar530754

Raish Khanji GTU 8th sem Internship Report.pdfRaishKhanji

Mathematical foundation machine learning.pdfTalhaShahid49

Compiler Design_Lexical Analysis phase.pptxRushaliDeshmukh2

π0.5: a Vision-Language-Action Model with Open-World GeneralizationNABLAS株式会社

Metal alkyne complexes.pptx in chemistrymee23nu

Introduction to Zoomlion Earthmoving.pptxAS1920

introduction to machine learining for beginersJoydebSheet

Smart Storage Solutions.pptx for production engineeringrushikeshnavghare94

some basics electrical and electronics knowledgenguyentrungdo88

Shortest path problem

2. PRESENTED TO: MAM MERYAM DEPARTMENT OF COMPUTER SCIENCE

3. GROUP MEMBERS: IFRA ILYAS (470) AQSA SHAUKAT (586) PAZEER ZARA (452) SAMRA ASLAM (427) AQSA ANWAR (453)

4. SHORTEST PATH PROBLEM

5. GRAPH:  A graph is a representation of a set of objects where some pairs of objects are connected by links.  Vertices: The interconnected objects are represented by mathematical abstractions called vertices.  Edges: The links that connect some pairs of vertices are called edges.

6. SHORTEST PATH PROBLEM :  The shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized. 

7. TYPES OF GRAPH: 1. Weighted graph 2. Un-weighted graph 3. Directed graph 4. Un-directed graph

8. TYPES OF GRAPHS:  Weighted: A graph is a weighted graph if a number (weight) is assigned to each edge. Example: Such weights might represent, for example, costs, lengths or capacities, etc.  Un-weighted: A graph is a unweighted graph if a number(weight) is not assigned to each edge.

9. TYPES OF GRAPHS:  Directed: An directed graph is one in which edges have orientation.  Un-directed: An undirected graph is one in which edges have no orientation.

10. SHORTEST PATH PROBLEM:  Given the graph below, suppose we wish to find the shortest path from vertex 1 to vertex 13.

11. EXAMPLE:  After some consideration, we may determine that the shortest path is as follows, with length 14  Other paths exists, but they are longer

12. NEGATIVE CYCLES:  Clearly, if we have negative vertices, it may be possible to end up in a cycle whereby each pass through the cycle decreases the total length  Thus, a shortest length would be undefined for such a graph  Consider the shortest path from vertex 1 to 4...  We will only consider non- negative weights.

13. SHORTEST PATH EXAMPLE:  Given:  Weighted Directed graph G = (V, E).  Source s, destination t.  Find shortest directed path from s to t. s 3 t 2 6 7 4 5 23 18 2 9 14 15 5 30 20 44 16 11 6 19 6 Cost of path s-2-3-5-t = 9 + 23 + 2 + 16 = 48.

14. DISCUSSION ITEMS  How many possible paths are there from s to t?  Can we safely ignore cycles? If so, how?  Any suggestions on how to reduce the set of possibilities? s 3 t 2 6 7 4 5 23 18 2 9 14 15 5 30 20 44 16 11 6 19 6

15. KEY OBSERVATION:  A key observation is that if the shortest path contains the node v, then:  It will only contain v once, as any cycles will only add to the length.  The path from s to v must be the shortest path to v from s.  The path from v to t must be the shortest path to t from v.

16. DIJKSTRA’S ALGORITHM:  Works when all of the weights are positive.  Provides the shortest paths from a source to all other vertices in the graph.  Can be terminated early once the shortest path to t is found if desired.

17. EXAMPLE:  Consider the graph:  the distances are appropriately initialized  all vertices are marked as being unvisited

18. EXAMPLE:  Visit vertex 1 and update its neighbours, marking it as visited  the shortest paths to 2, 4, and 5 are updated

19. EXAMPLE:  The next vertex we visit is vertex 4  vertex 5 1 + 11 ≥ 8 don’t update  vertex 7 1 + 9 < ∞ update  vertex 8 1 + 8 < ∞ update

20. EXAMPLE:  Next, visit vertex 2  vertex 3 4 + 1 < ∞ update  vertex 4 already visited  vertex 5 4 + 6 ≥ 8 don’t update  vertex 6 4 + 1 < ∞ update

21. EXAMPLE:  Next, we have a choice of either 3 or 6  We will choose to visit 3  vertex 5 5 + 2 < 8 update  vertex 6 5 + 5 ≥ 5 don’t update

22. EXAMPLE:  We then visit 6  vertex 8 5 + 7 ≥ 9 don’t update  vertex 9 5 + 8 < ∞ update

23. EXAMPLE:  Next, we finally visit vertex 5:  vertices 4 and 6 have already been visited  vertex 7 7 + 1 < 10 update  vertex 8 7 + 1 < 9 update  vertex 9 7 + 8 ≥ 13 don’t update

24. EXAMPLE:  Given a choice between vertices 7 and 8, we choose vertex 7  vertices 5 has already been visited  vertex 8 8 + 2 ≥ 8 don’t update

25. EXAMPLE:  Next, we visit vertex 8:  vertex 9 8 + 3 < 13 update

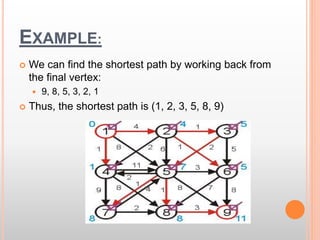
26. EXAMPLE:  Finally, we visit the end vertex  Therefore, the shortest path from 1 to 9 has length 11

27. EXAMPLE:  We can find the shortest path by working back from the final vertex:  9, 8, 5, 3, 2, 1  Thus, the shortest path is (1, 2, 3, 5, 8, 9)

Shortest path problem

Recommended

More Related Content

What's hot (20)

Viewers also liked (20)

Similar to Shortest path problem (20)

Recently uploaded (20)

Shortest path problem