Signal Processing Course : Theory for Sparse Recovery

1
Sparse
Recovery
Gabriel Peyré
www.numerical-tours.com

1
Example: Regularization
Inverse problem: measurements y = Kf0 + w
f0 Kf0
K
K : RN0 RP , P N0

1
f0 Kf0
K
K : RN0 RP , P N0

Model: f0 = x0 sparse in dictionary RN0 N
,N N0 .
x0 RN f0 = x0 R N0 K y = Kf0 + w RP
coe cients image w observations

= K ⇥ ⇥ RP N

1
f0 Kf0
K
K : RN0 RP , P N0

Model: f0 = x0 sparse in dictionary RN0 N
,N N0 .
x0 RN f0 = x0 R N0 K y = Kf0 + w RP
coe cients image w observations

= K ⇥ ⇥ RP N

Sparse recovery: f = x where x solves
1
min ||y x||2 + ||x||1
x RN 2
Fidelity Regularization

Variations and Stability
Data: f0 = x0

Observations: y = x0 + w
1
Recovery: x ⇥ argmin || x y||2 + ||x||1 (P (y))
x RN 2

Data: f0 = x0

1
0+

x RN 2

x argmin ||x||1 (no noise) (P0 (y))
x=y

Data: f0 = x0

1
0+

x RN 2

x argmin ||x||1 (no noise) (P0 (y))
x=y

Questions:
– Behavior of x with respect to y and .

– Criterion to ensure x = x0 when w = 0 and = 0+ .
– Criterion to ensure ||x x0 || = O(||w||).

Numerical Illustration
s=3 s=3 s=6 s=6

0.5 0.5 y = s=3 0 + w, ||x0 ||0 =0.5
x s=3 s, 2 R50⇥200 s=6
0.5 s=6 Gaussian.
0 0
s=3 s=6
0 0
0.5 0.5 0.5 0.5

−0.5 −0.5 −0.5 −0.5
0 0 0 0

−1 −1
−0.5 10
−0.5 20 10 30 20 40 30 50 40 60 50 60 −0.5 10
−0.5 2010 3020 4030 5040 6050 60

−1 −1 s=13 s=13 s=25 s=25
10 20 10 30 20 40 30 50 40 60 50 60 10 2010 3020 4030 5040 6050 60
1 1
s = 13 1.5 1.5 s = 25
s=13 s=13 1 1 s=25 s=25
0.5 0.5
1 1 0.5 0.5
1.5 1.5
0 0
0 0 1 1
0.5 0.5 −0.5 −0.5
0.5 0.5
−0.5 −0.5 −1 −1
0 0
0 0 −1.5 −1.5
−0.5 −0.5
20 40
20 60
40 80
60 100
80 100 −1 20 40 2060 4080 60 80 100 120 140
100 120 140
! Mapping ! x? looks polygonal.
−0.5 −0.5 −1
−1.5 −1.5
! If x0 sparse and 80 100chosen, sign(x?60 = sign(x0140
20 40 60
well )
2060 4080 10080 100 120
).
20 40 60 80 100 20 40 120 140

Overview

• Polytope Noiseless Recovery

• Local Behavior of Sparse Regularization

• Robustness to Small Noise

• Robustness to Bounded Noise

• Compressed Sensing RIP Theory

Polytopes Approach

= ( i )i R2 3
3 2

1

x0 x0
1
y x (y)
3
B = {x ||x||1 } 2
(B )
= ||x0 ||1

x0 solution of P0 ( x0 ) ⇥ x0 ⇤ (B )

min ||x||1
x=y

Polytopes Approach

= ( i )i R2 3
3 2

1

x0 x0
1
y x (y)
3
B = {x ||x||1 } 2
(B )
= ||x0 ||1


min ||x||1 (P0 (y))
x=y

Proof
= Suppose x0 not solution, show (x0 ) int( B )
x0 = z,
⇥z, such that
||z||1 = (1 )||x0 ||1 .
For any h = Im( ) such that ||h||1 < + ||
|| 1,1
(x0 ) + h = (z + )
||z + ⇥||1 ||z|| + || +
h||1 (1 )||x0 ||1 + || ||1,1 ||h||1 < ||x0 ||1
= (x0 ) + h (B )

Proof
= Suppose x0 not solution, show (x0 ) int( B )
x0 = z,
⇥z, such that
||z||1 = (1 )||x0 ||1 .
For any h = Im( ) such that ||h||1 < + ||
|| 1,1
(x0 ) + h = (z + )
||z + ⇥||1 ||z|| + || +
h||1 (1 )||x0 ||1 + || ||1,1 ||h||1 < ||x0 ||1
= (x0 ) + h (B )
(B )
= Suppose (x0 ) int( B ) 0
x0
Then ⇥z, x0 = (1 ) z and ||z||1 < ||x0 ||1 . z
||(1 )z||1 < ||x0 ||1 so x0 is not a solution.

Basis-Pursuit Mapping in 2-D
= ( i )i R2 3

C(0,1,1) 2
3
K(0,1,1)
1

y x (y)

2-D quadrant 2-D cones
Ks = ( i si )i R3 i 0 Cs = Ks

Basis-Pursuit Mapping in 3-D
= ( i )i R3 N

j

i

N Cs
R
y x (y)
k

Delaunay paving of the sphere with spherical triangles Cs
Empty spherical caps property

Polytope Noiseless Recovery
Counting faces of random polytopes: [Donoho]
All x0 such that ||x0 ||0 Call (P/N )P are identiﬁable.
Most x0 such that ||x0 ||0 Cmost (P/N )P are identiﬁable.
1

Call (1/4) 0.065 0.9

0.8

Cmost (1/4) 0.25 0.7

0.6

0.5

Sharp constants. 0.4

0.3

No noise robustness. 0.2

0.1

0
50 100 150 200 250 300 350 400

RIP All Most

First Order CNS Condition
1
x ⇥ argmin E(x) = || x y||2 + ||x||1
x RN 2
Support of the solution: I = {i ⇥ {0, . . . , N 1} xi ⇤= 0}

First order condition: x solution of P (y) 0 E(x )
sI = sign(xI ),
( x y) + s = 0 where
||sI c || 1

First Order CNS Condition
1
x ⇥ argmin E(x) = || x y||2 + ||x||1
x RN 2
Support of the solution: I = {i ⇥ {0, . . . , N 1} xi ⇤= 0}

First order condition: x solution of P (y) 0 E(x )
sI = sign(xI ),
( x y) + s = 0 where
||sI c || 1
1
Note: sI c = Ic ( x y)

Theorem: || Ic ( x y)|| x solution of P (y)

Local Parameterization
If I has full rank: +
I =( I I)
1
I

( x y) + s = 0 = xI = + y
I ( I I ) 1 sI
Implicit equation

I =( I I)
1
I

( x y) + s = 0 = xI = + y I ( I I ) 1 sI
Implicit equation
Given y compute x compute (s, I).
Deﬁne x ¯ (¯)I = + y
ˆ y ¯(
I ¯ II ) 1 sI
x ¯ (¯)I c = 0
ˆ y
By construction x (y) = x .
ˆ

I =( I I)
1
I

( x y) + s = 0 =xI = + y I ( I I ) 1 sI
Implicit equation
Given y compute x compute (s, I). 2 1 2
¯( 1
Deﬁne x ¯ (¯)I = I y
ˆ y +
¯ I I)
1
sI 1
2 ||x ||0= 0
x ¯ (¯)I c = 0
ˆ y 2
1
By construction x (y) = x .
ˆ 1
2 1 2

Theorem: For (y, ) 2 H, let x? be a solution of P (y),
/
such that I is full rank, I = supp(x? ),
for ( ¯ , y ) close to ( , y), x ¯ (¯) is solution of P ¯ (¯)
¯ ˆ y y

Remark: the theorem holds outside a union of hyperplanes.

Full Rank Condition
Lemma: There exists x? such that ker( I) = {0}.

! if ker( I ) 6= {0}, x? not unique.

Full Rank Condition

Proof: If ker( I) 6= {0}, let ⌘I 2 ker( I) 6= 0.
Deﬁne 8 t 2 R, xt = x? + t⌘.

Full Rank Condition

Deﬁne 8 t 2 R, xt = x? + t⌘.
Let t0 the smallest |t| s.t. sign(xt ) 6= sign(x? ).

xt

t
t0 0

Full Rank Condition

Deﬁne 8 t 2 R, xt = x? + t⌘.

xt = x? and same sign: xt
8 |t| < t0 , xt is solution.
t
t0 0

Full Rank Condition

Deﬁne 8 t 2 R, xt = x? + t⌘.

xt = x? and same sign: xt
8 |t| < t0 , xt is solution.

By continuity, xt0 solution. t
t0 0
and | supp(xt0 )| < | supp(x? )|.

Proof
x ¯ (¯)I =
ˆ y +
¯ ¯( ) 1 sI I = supp(s)
I y I I
To show: 8 j 2 I,
/ ds (¯, ¯ ) = |h'j , y
j y ¯ I x ¯ (¯)i| 6
ˆ y

Proof
x ¯ (¯)I =
ˆ y +
¯ ¯( ) 1 sI I = supp(s)
I y I I
To show: 8 j 2 I,
/ ds (¯, ¯ ) = |h'j , y
j y ¯ I x ¯ (¯)i| 6
ˆ y

Case 1: ds (y, ) <
j
! ok, by continuity.

Proof
x ¯ (¯)I =
ˆ y +
¯ ¯( ) 1 sI I = supp(s)
I y I I
To show: 8 j 2 I,
/ ds (¯, ¯ ) = |h'j , y
j y ¯ I x ¯ (¯)i| 6
ˆ y

Case 1: ds (y, ) <
j Case 2: ds (y, ) = and 'j 2 Im(
j I)
! ok, by continuity. then ds (¯, ¯ ) = ¯ ! ok.
j y

Proof
x ¯ (¯)I =
ˆ y +
¯ ¯( ) 1 sI I = supp(s)
I y I I
To show: 8 j 2 I,
/ ds (¯, ¯ ) = |h'j , y
j y ¯ I x ¯ (¯)i| 6
ˆ y

Case 1: ds (y, ) <
j I)
j y

Case 3: ds (y, ) = and
j
'j 2 Im( I )
/
! exclude this case.

Proof
x ¯ (¯)I =
ˆ y +
¯ ¯( ) 1 sI I = supp(s)
I y I I
To show: 8 j 2 I,
/ ds (¯, ¯ ) = |h'j , y
j y ¯ I x ¯ (¯)i| 6
ˆ y

Case 1: ds (y, ) <
j I)
j y

Case 3: ds (y, ) = and
j
'j 2 Im( I )
/

Exclude hyperplanes:
[
H= {Hs,j 'j 2 Im( I )}
/
Hs,j = (y, ) ds (¯, ¯ ) =
j y

Proof
x ¯ (¯)I =
ˆ y +
¯ ¯( ) 1 sI I = supp(s)
I y I I
To show: 8 j 2 I,
/ ds (¯, ¯ ) = |h'j , y
j y ¯ I x ¯ (¯)i| 6
ˆ y

Case 1: ds (y, ) <
j I)
j y

Case 3: ds (y, ) = and H;,j
j
'j 2 Im( I )
/
x?= 0
[
H= {Hs,j 'j 2 Im( I )}
/
Hs,j = (y, ) ds (¯, ¯ ) =
j y

Proof
x ¯ (¯)I =
ˆ y +
¯ ¯( ) 1 sI I = supp(s)
I y I I
To show: 8 j 2 I,
/ ds (¯, ¯ ) = |h'j , y
j y ¯ I x ¯ (¯)i| 6
ˆ y

Case 1: ds (y, ) <
j I)
j y

Case 3: ds (y, ) = and H;,j
j
'j 2 Im( I )
/
! exclude this case. HI,j
x?= 0
[
H= {Hs,j 'j 2 Im( I )}
/
Hs,j = (y, ) ds (¯, ¯ ) =
j y

Local Affine Maps
Local parameterization: x ¯ (¯)I =
ˆ y +
¯ ¯( I)
1
I y I sI
Under uniqueness assumption:
y x
are piecewise a ne functions.
x
x1 breaking points

change of support of x
x0
(BP sol.)
x k
=0
0 =0 k

x2

Projector
E (x) = 1 || x
2 y||2 + ||x||1
Proposition: If x1 and x2 minimize E ,
then x1 = x2 .

Corrolary: µ(y) = x1 = x2 is uniquely deﬁned.

Projector
E (x) = 1 || x
2 y||2 + ||x||1
then x1 = x2 .


Proof: x3 = (x1 + x2 )/2 is solution and if x1 6= x2 ,
2||x3 ||1 6 ||x1 ||1 + ||x2 ||1
2|| x3 y||2 < || x1 y||2 + || x2 y||2
E (x3 ) < E (x1 ) = E (x2 ) =) contradiction.

Projector
E (x) = 1 || x
2 y||2 + ||x||1
then x1 = x2 .


Proof: x3 = (x1 + x2 )/2 is solution and if x1 6= x2 ,
2||x3 ||1 6 ||x1 ||1 + ||x2 ||1
2|| x3 y||2 < || x1 y||2 + || x2 y||2
E (x3 ) < E (x1 ) = E (x2 ) =) contradiction.

For (¯, ) close to (y, ) 2 H:
y / µ(¯) = PI (¯)
y y dI
+ +,⇤
= I I = I sI
PI : orthogonal projector on { x supp(x) = I}.

Uniqueness Sufficient Condition

E (x) = 1 || x
2 y||2 + ||x||1


E (x) = 1 || x
2 y||2 + ||x||1

Theorem: If I has full rank and || I c ( x y)|| <
then x? is the unique minimizer of E .


E (x) = 1 || x
2 y||2 + ||x||1

Theorem: If I has full rank and || I c ( x y)|| <
then x? is the unique minimizer of E .

Proof: Let x? be a minimizer.
˜
Then ?
x = x =)
˜ ? x?
˜I x? 2 ker(
I I) = {0}.
|| Ic ( x?
˜ y)||1 = || Ic ( x? y)||1 <
=) supp(˜? ) ⇢ I
x
=) x? = x?
˜

Robustness to Small Noise
Identiﬁability crition: [Fuchs]
For s ⇥ { 1, 0, +1}N , let I = supp(s)
+,
F(s) = || I sI || where ⇥I = Ic I
( I is assumed to have full rank)
+
I =( I I)
1
I satisﬁes +
I I = IdI

Robustness to Small Noise
Identiﬁability crition: [Fuchs]
For s ⇥ { 1, 0, +1}N , let I = supp(s)
+,
F(s) = || I sI || where ⇥I = Ic I
( I is assumed to have full rank)
+
I =( I I)
1
I satisﬁes +
I I = IdI

Theorem: If F (sign(x0 )) < 1, T = min |x0,i |
i I
If ||w||/T is small enough and ||w||, then
x0 + +
I w ( I I)
1
sign(x0,I )
is the unique solution of P (y).

⇥ If ||w|| small enough, ||x x0 || = O(||w||).

Geometric Interpretation
+,
dI = sI
F(s) = || I sI || = max | dI , j ⇥|
I i
j /I

where dI deﬁned by: dI = I( I I)
1
sI
i I, dI , i = si j

+,
dI = sI
F(s) = || I sI || = max | dI , j ⇥|
I i
j /I

1
sI
i I, dI , i = si j

Condition F (s) < 1: no vector j inside the cap Cs .

dI
j Cs
i

| dI , ⇥| < 1

+,
dI = sI
F(s) = || I sI || = max | dI , j ⇥|
I i
j /I

1
sI
i I, dI , i = si j

Condition F (s) < 1: no vector j inside the cap Cs .
dI
j dI
i k | dI , ⇥| < 1 j Cs
i

| dI , ⇥| < 1

Sketch of Proof
Local candidate: implicit equation x = x(sign(x ))
ˆ
where x(s)I =
ˆ +
I y ( I I)
1
sI , I = supp(s)
⇥ To prove: x = x(sign(x0 )) is the unique solution of P (y).
ˆ ˆ

Sketch of Proof
ˆ
where x(s)I =
ˆ +
I y ( I I)
1
sI , I = supp(s)
ˆ ˆ

Sign consistency: sign(ˆ) = sign(x0 )
x (C1 )
y = x0 + w = x = x0 +
ˆ +
I w ( I I)
1
sI
,2 ||w|| + ||( I)
+
|| I || I
1
|| , <T = (C1 )

Sketch of Proof
ˆ
where x(s)I =
ˆ +
I y ( I I)
1
sI , I = supp(s)
ˆ ˆ

Sign consistency: sign(ˆ) = sign(x0 )
x (C1 )
y = x0 + w = x = x0 +
ˆ +
I w ( I I)
1
sI
,2 ||w|| + ||( I)
+
|| I || I
1
|| , <T = (C1 )

First order conditions: || Ic ( ˆ
x y)|| < (C2 )
|| Ic ( I
+
I Id)||2, ||w|| (1 F (s)) < 0 = (C2 )

Sketch of Proof (cont)

,2 ||w|| + ||( I)
+ 1
|| I || I || , <T = x is
ˆ
the solution
Ic ( Id)||2, ||w|| (1 F (s)) < 0
+
|| I I


,2 ||w|| + ||( I)
+ 1
|| I || I || , <T = x is
ˆ
the solution
Ic ( Id)||2, ||w|| (1 F (s)) < 0
+
|| I I

For ||w||/T < ⇥max , one can choose ||w||/T
such that x is the solution of P (y).
ˆ
||w||

0
=
⇥⇤
T max

|
|w

||w
||
+⇥
⇤=
T


,2 ||w|| + ||( I)
+ 1
|| I || I || , <T = x is
ˆ
the solution
Ic ( Id)||2, ||w|| (1 F (s)) < 0
+
|| I I

For ||w||/T < ⇥max , one can choose ||w||/T
such that x is the solution of P (y).
ˆ
||w||

0
=
⇥⇤
||ˆ
x x0 || || +
+ ||( I
I w|| I)
1
|| ,2 T max
= O(||w||)

|
|w

||w
||
=⇥ ||ˆ
x x0 || = O(||w||)

+⇥
⇤=
T

Robustness to Bounded Noise
Exact Recovery Criterion (ERC): [Tropp]
For a support I ⇥ {0, . . . , N 1} with I full rank,
ERC(I) = || I || , where ⇥I = Ic
+,
I

= || +
I Ic ||1,1 = max ||
c
+
I j ||1
j I

(use ||(aj )j ||1,1 = maxj ||aj ||1 )

Relation with F criterion: ERC(I) = max F(s)
s,supp(s) I

Robustness to Bounded Noise
Exact Recovery Criterion (ERC): [Tropp]
For a support I ⇥ {0, . . . , N 1} with I full rank,
ERC(I) = || I || , where ⇥I = Ic
+,
I

= || +
I Ic ||1,1 = max ||
c
+
I j ||1
j I

(use ||(aj )j ||1,1 = maxj ||aj ||1 )

Relation with F criterion: ERC(I) = max F(s)
s,supp(s) I

Theorem: If ERC(supp(x0 )) < 1 and ||w||, then
x is unique, satisﬁes supp(x ) supp(x0 ), and
||x0 x || = O(||w||)

Sketch of Proof
Restricted recovery:
1
x ⇥ argmin || x
ˆ y||2 + ||x||1
supp(x) I 2
⇥ To prove: x is the unique solution of P (y).
ˆ

Sketch of Proof
1
x ⇥ argmin || x
ˆ y||2 + ||x||1
supp(x) I 2
ˆ
Implicit equation: xI =
ˆ +
I y ( I I)
1
sI
Important: s = sign(ˆ) is not equal to sign(x ).
x

Sketch of Proof
1
x ⇥ argmin || x
ˆ y||2 + ||x||1
supp(x) I 2
ˆ
ˆ +
I y ( I I)
1
sI
x

x y)|| < (C2 )
|| Ic ( I
+
I Id)||2, ||w|| (1 F (s)) < 0 = (C2 )

Sketch of Proof
1
x ⇥ argmin || x
ˆ y||2 + ||x||1
supp(x) I 2
ˆ
ˆ +
I y ( I I)
1
sI
x

x y)|| < (C2 )
|| Ic ( I
+
I Id)||2, ||w|| (1 F (s)) < 0 = (C2 )

Since s is arbitrary: ERC(I) < 1 = F (s) < 1

Hence, choosing ||w|| implies (C2 ).

Weak ERC
For A = (ai )i , B = (bi )i , where ai , bi RP ,
(A, B) = max | ai , bj ⇥|
j
i I
(A) = max | ai , aj ⇥|
j
i=j

Weak Exact Recovery Criterion: [Gribonval,Dossal]
Denoting = ( i )N 1 where
i=0 i RP
( I, Ic )
if ( I) <1
w-ERC(I) = 1 ( I)
+ otherwise.

Theorem: F(s) ERC(I) w-ERC(I) (for I = supp(s))

Proof


ERC(I) = max || +
I j ||1 ||( I I)
1
||1,1 max || I j ||1
j /I j /I

max || I ⇥j ||1 = max | ⇥i , ⇥j ⇥| = ( I, Ic )
j /I j /I
i m

Proof


ERC(I) = max || +
I j ||1 ||( I I)
1
||1,1 max || I j ||1
j /I j /I

max || I ⇥j ||1 = max | ⇥i , ⇥j ⇥| = ( I, Ic )
j /I j /I
i m
One has I I = Id H, if ||H||1,1 < 1,
( I I)
1
= (Id H) 1
= Hk
k 0
1
I) =
1
||( ||1,1 ||H||k
I 1,1
1 ||H||1,1
k 0

||H||1,1 = max | ⇥i , ⇥j ⇥| = ( I)
i I
j=i

Example: Random Matrix

P = 200, N = 1000
1

0.8

0.6

0.4

0.2

0

0 10 20 30 40 50
w-ERC < 1 F <1
ERC < 1 x = x0

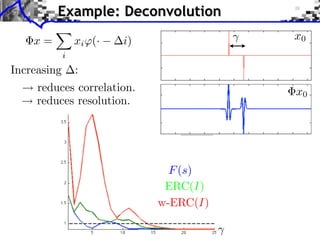
Example: Deconvolution
⇥x = xi (· i) x0
i
Increasing :
reduces correlation. x0
reduces resolution.

F (s)
ERC(I)
w-ERC(I)

Coherence Bounds
Mutual coherence: µ( ) = max | i, j ⇥|
i=j

|I|µ( )
Theorem: F(s) ERC(I) w-ERC(I)
1 (|I| 1)µ( )

Coherence Bounds
i=j

|I|µ( )
1 (|I| 1)µ( )

1 1
Theorem: If ||x0 ||0 < 1+ and ||w||,
2 µ( )
one has supp(x ) I, and ||x0 x || = O(||w||)

Coherence Bounds
i=j

|I|µ( )
1 (|I| 1)µ( )

1 1
Theorem: If ||x0 ||0 < 1+ and ||w||,
2 µ( )
one has supp(x ) I, and ||x0 x || = O(||w||)

N P
One has: µ( )
P (N 1) Optimistic setting:
For Gaussian matrices: ||x0 ||0 O( P )
µ( ) log(P N )/P
For convolution matrices: useless criterion.

Coherence - Examples
Incoherent pair of orthobases: Diracs/Fourier
2i
1 = {k ⇤⇥ [k m]}m 2 = k N 1/2
e N mk
m
=[ 1, 2] RN 2N

2i
1 = {k ⇤⇥ [k m]}m 2 = k N 1/2
e N mk
m
=[ 1, 2] RN 2N

1
min ||y x||2 + ||x||1
x R2N 2
1
min ||y 1 x1 2 x2 ||2 + ||x1 ||1 + ||x2 ||1
x1 ,x2 RN 2

= +

2i
1 = {k ⇤⇥ [k m]}m 2 = k N 1/2
e N mk
m
=[ 1, 2] RN 2N

1
min ||y x||2 + ||x||1
x R2N 2
1
min ||y 1 x1 2 x2 ||2 + ||x1 ||1 + ||x2 ||1
x1 ,x2 RN 2

= +

1
µ( ) = = separates up to N /2 Diracs + sines.
N

CS with RIP
1
recovery:
y = x0 + w
x⇥
argmin ||x||1 where
|| x y|| ||w||
1
⇥ argmin || x y||2 + ||x||1
x 2
Restricted Isometry Constants:
⇥ ||x||0 k, (1 k )||x||2 || x||2 (1 + k )||x||2

CS with RIP
1
recovery:
y = x0 + w
x⇥
argmin ||x||1 where
|| x y|| ||w||
1
⇥ argmin || x y||2 + ||x||1
x 2
Restricted Isometry Constants:
⇥ ||x||0 k, (1 k )||x||2 || x||2 (1 + k )||x||2

Theorem: If 2k 2 1, then [Candes 2009]
C0
||x0 x || ⇥ ||x0 xk ||1 + C1
k
where xk is the best k-term approximation of x0 .

Elements of Proof
Reference: E. J. Cand`s, CRAS, 2006
e
k elements

{0, . . . , N 1} = T0 ⇥ T1 ⇥ . . . ⇥ Tm h=x x0
largest largest xk = xT0
of x0 of hT0c

Optimality conditions: ||hT0 ||1
c ||hT0 ||1 + 2||xT0 ||1
c

Explicit constants: 2 2k
C0 =
||x0 x || ⇥ ||x0 xk ||1 + C1 1 2k
s
1 + 2k
2 =2
C0 = C1 = 1
1 1 ⇥ 2k

Singular Values Distributions
Eigenvalues of I I with |I| = k are essentially in [a, b]
a = (1 )2 and b = (1 )2 where = k/P
When k = P + , the eigenvalue distribution tends to
1
f (⇥) = (⇥ b)+ (a ⇥)+ [Marcenko-Pastur]
1.5
2⇤ ⇥ P=200, k=10

P=200, k=10

f ( )
1.5
1

1
0.5

P = 200, k = 10
0.5
0
0 0.5 1 1.5 2 2.5
0
0 0.5 1 P=200, k=30 1.5 2 2.5

1
P=200, k=30
0.8
1

0.6
0.8

0.4

k = 30
0.6

0.2
0.4

0
0.2
0 0.5 1 1.5 2 2.5
0
0 0.5 1 P=200, k=50 1.5 2 2.5

P=200, k=50
0.8

0.8
0.6

0.6
0.4
Large deviation inequality [Ledoux]
0.4
0.2

RIP for Gaussian Matrices

Link with coherence: µ( ) = max | i, j ⇥|
i=j
2 = µ( )
k (k 1)µ( )


i=j
2 = µ( )
k (k 1)µ( )

For Gaussian matrices:
µ( ) log(P N )/P


i=j
2 = µ( )
k (k 1)µ( )

For Gaussian matrices:
µ( ) log(P N )/P
Stronger result:
C
Theorem: If k P
log(N/P )
then 2k 2 1 with high probability.

Numerics with RIP
Stability constant of A:
(1 ⇥1 (A))|| ||2 ||A ||2 (1 + ⇥2 (A))|| ||2

smallest / largest eigenvalues of A A

Numerics with RIP
Stability constant of A:
(1 ⇥1 (A))|| ||2 ||A ||2 (1 + ⇥2 (A))|| ||2

smallest / largest eigenvalues of A A

Upper/lower RIC:
i
k = max i( I) ˆ2
|I|=k k

k = min( k ,
1
k)
2
2 1 ˆ2
k

Monte-Carlo estimation:
ˆk k
k

Conclusion
s=3 s=6

Local behavior:
0.5 0.5
! x? polygonal.
0
? 0
y ! x piecewise a ne.
−0.5 −0.5

−1
10 20 30 40 50 60 10 20 30 40 50 60

s=13 s=25
1
1.5
1
0.5
0.5
0
0
−0.5

−0.5 −1
−1.5

20 40 60 80 100 20 40 60 80 100 120 140

Conclusion
s=3 s=6

Local behavior:
0.5 0.5
! x? polygonal.
0
? 0
−0.5 −0.5

Noiseless recovery:
−1
10 20 30 40 50 60 10 20 30 40 50 60
() geometry of polytopes.
s=13 s=25
1
1.5
1
0.5
0.5
0
0
−0.5 x0
−0.5 −1
−1.5

20 40 60 80 100 20 40 60 80 100 120 140

Conclusion
s=3 s=6

Local behavior:
0.5 0.5
! x? polygonal.
0
? 0
−0.5 −0.5

Noiseless recovery:
−1
10 20 30 40 50 60 10 20 30 40 50 60
() geometry of polytopes.
s=13 s=25

Small noise: 1 1.5
1
! sign stability.
0.5
0.5
0

Bounded noise:
0
−0.5 x0
−0.5 −1
! support inclusion. −1.5

20 40 60 80 100 20 40 60 80 100 120 140
RIP-based:
! no support stability, L1 bounds.

Signal Processing Course : Theory for Sparse Recovery

Recommended

More Related Content

What's hot (19)

Viewers also liked (18)

Similar to Signal Processing Course : Theory for Sparse Recovery (20)

More from Gabriel Peyré (20)

Signal Processing Course : Theory for Sparse Recovery