More Related Content
What's hot (20)
Similar to Skiena algorithm 2007 lecture02 asymptotic notation (20)
More from zukun (20)
Recently uploaded (20)
Skiena algorithm 2007 lecture02 asymptotic notation
- 1. Lecture 2: Asymptotic Notation Steven Skiena Department of Computer Science State University of New York Stony Brook, NY 11794–4400 http://www.cs.sunysb.edu/∼skiena
- 2. Problem of the Day The knapsack problem is as follows: given a set of integers S = {s1, s2, . . . , sn}, and a given target number T , find a subset of S which adds up exactly to T . For example, within S = {1, 2, 5, 9, 10} there is a subset which adds up to T = 22 but not T = 23. Find counterexamples to each of the following algorithms for the knapsack problem. That is, give an S and T such that the subset is selected using the algorithm does not leave the knapsack completely full, even though such a solution exists.
- 3. Solution • Put the elements of S in the knapsack in left to right order if they fit, i.e. the first-fit algorithm? • Put the elements of S in the knapsack from smallest to largest, i.e. the best-fit algorithm? • Put the elements of S in the knapsack from largest to smallest?
- 4. The RAM Model of Computation Algorithms are an important and durable part of computer science because they can be studied in a machine/language independent way. This is because we use the RAM model of computation for all our analysis. • Each “simple” operation (+, -, =, if, call) takes 1 step. • Loops and subroutine calls are not simple operations. They depend upon the size of the data and the contents of a subroutine. “Sort” is not a single step operation.
- 5. • Each memory access takes exactly 1 step. We measure the run time of an algorithm by counting the number of steps, where: This model is useful and accurate in the same sense as the flat-earth model (which is useful)!
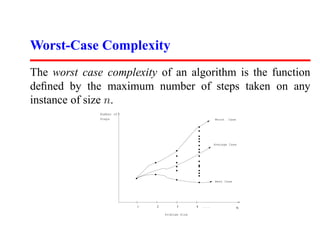
- 6. Worst-Case Complexity The worst case complexity of an algorithm is the function defined by the maximum number of steps taken on any instance of size n. Number of Steps Worst Case Average Case . . Best Case 1 2 3 4 ...... N Problem Size
- 7. Best-Case and Average-Case Complexity The best case complexity of an algorithm is the function defined by the minimum number of steps taken on any instance of size n. The average-case complexity of the algorithm is the function defined by an average number of steps taken on any instance of size n. Each of these complexities defines a numerical function: time vs. size!
- 8. Exact Analysis is Hard! Best, worst, and average are difficult to deal with precisely because the details are very complicated: 1 2 3 4 ...... It easier to talk about upper and lower bounds of the function. Asymptotic notation (O, Θ, Ω) are as well as we can practically deal with complexity functions.
- 9. Names of Bounding Functions • g(n) = O(f (n)) means C × f (n) is an upper bound on g(n). • g(n) = Ω(f (n)) means C ×f (n) is a lower bound on g(n). • g(n) = Θ(f (n)) means C1 × f (n) is an upper bound on g(n) and C2 × f (n) is a lower bound on g(n). C, C1, and C2 are all constants independent of n.
- 10. O, Ω, and Θ c1*g(n) c*g(n) f(n) f(n) f(n) c*g(n) c2*g(n) n n n n0 n0 n0 (a) (b) (c) The definitions imply a constant n0 beyond which they are satisfied. We do not care about small values of n.
- 11. Formal Definitions • f (n) = O(g(n)) if there are positive constants n0 and c such that to the right of n0, the value of f (n) always lies on or below c · g(n). • f (n) = Ω(g(n)) if there are positive constants n0 and c such that to the right of n0, the value of f (n) always lies on or above c · g(n). • f (n) = Θ(g(n)) if there exist positive constants n0 , c1, and c2 such that to the right of n0 , the value of f (n) always lies between c1 · g(n) and c2 · g(n) inclusive.
- 12. Big Oh Examples 3n2 − 100n + 6 = O(n2 ) because 3n2 > 3n2 − 100n + 6 3n2 − 100n + 6 = O(n3 ) because .01n3 > 3n2 − 100n + 6 3n2 − 100n + 6 = O(n) because c · n < 3n2 when n > c Think of the equality as meaning in the set of functions.
- 13. Big Omega Examples 3n2 − 100n + 6 = Ω(n2 ) because 2.99n2 < 3n2 − 100n + 6 3n2 − 100n + 6 = Ω(n3 ) because 3n2 − 100n + 6 < n3 1010 3n − 100n + 6 = Ω(n) because 10 n < 3n2 − 100 + 6 2
- 14. Big Theta Examples 3n2 − 100n + 6 = Θ(n2 ) because O and Ω 3n2 − 100n + 6 = Θ(n3 ) because O only 3n2 − 100n + 6 = Θ(n) because Ω only
- 15. Big Oh Addition/Subtraction Suppose f (n) = O(n2 ) and g(n) = O(n2 ). • What do we know about g (n) = f (n) + g(n)? Adding the bounding constants shows g (n) = O(n2 ). • What do we know about g (n) = f (n) − |g(n)|? Since the bounding constants don’t necessary cancel, g (n) = O(n2 ) We know nothing about the lower bounds on g and g because we know nothing about lower bounds on f and g.
- 16. Big Oh Multiplication by Constant Multiplication by a constant does not change the asymptotics: O(c · f (n)) → O(f (n)) Ω(c · f (n)) → Ω(f (n)) Θ(c · f (n)) → Θ(f (n))
- 17. Big Oh Multiplication by Function But when both functions in a product are increasing, both are important: O(f (n)) ∗ O(g(n)) → O(f (n) ∗ g(n)) Ω(f (n)) ∗ Ω(g(n)) → Ω(f (n) ∗ g(n)) Θ(f (n)) ∗ Θ(g(n)) → Θ(f (n) ∗ g(n))