Soft Computering Technics - Unit2

SOFT COMUTING TECHNICS

WELCOME

Soft Computing Technics

Presented by
 Rm.Sumanth
 P.Ganga Bashkar
&
 Habeeb Khan
 Rahim Khan

A mini Classroom Project review on
submitted to
MADINA ENGINEERING COLLEGE, KADPA.

in partial fulfillment of the requirements for the award of the
degree of
BATCHLOR OF TECHNOLOGY
in

ELECTRICAL & ELECTRONICS ENGINEERING

by

RM.SUMANTH
11725A0201
Mr.P.Ganga Bashkar,B.Tech,
Senior Technical Student,
Dept. of EEE Madina Engg.College
3

11/26/13

Machine Learning

Neural Networks

Introduction

∗ Artificial Neural Network is based on the biological
nervous system as Brain
∗ It is composed of interconnected computing units
called neurons
∗ ANN like human, learn by examples

Why Artificial Neural Networks?
There are two basic reasons why we are interested in
building artificial neural networks (ANNs):
∗ Technical viewpoint: Some problems such as
character recognition or the prediction of future
states of a system require massively parallel and
adaptive processing.
∗ Biological viewpoint: ANNs can be used to
replicate and simulate components of the human
(or animal) brain, thereby giving us insight into
natural information processing.
6

Science: Model how biological neural
systems, like human brain, work?
 How do we see?
 How is information stored
in/retrieved from memory?
 How do you learn to not to touch
fire?
 How do your eyes adapt to the
amount of light in the environment?
 Related fields: Neuroscience,
Computational Neuroscience,
Psychology, Psychophysiology,
Cognitive Science, Medicine, Math,
Physics.
7

Brief History
Old Ages:
∗ Association (William James; 1890)
∗ McCulloch-Pitts Neuron (1943,1947)
∗ Perceptrons (Rosenblatt; 1958,1962)
∗ Adaline/LMS (Widrow and Hoff; 1960)
∗ Perceptrons book (Minsky and Papert; 1969)
Dark Ages:
∗ Self-organization in visual cortex (von der Malsburg; 1973)
∗ Backpropagation (Werbos, 1974)
∗ Foundations of Adaptive Resonance Theory (Grossberg; 1976)
∗ Neural Theory of Association (Amari; 1977)
8

History
Modern Ages:
∗ Adaptive Resonance Theory (Grossberg; 1980)
∗ Hopfield model (Hopfield; 1982, 1984)
∗ Self-organizing maps (Kohonen; 1982)
∗ Reinforcement learning (Sutton and Barto; 1983)
∗ Simulated Annealing (Kirkpatrick et al.; 1983)
∗ Boltzmann machines (Ackley, Hinton, Terrence; 1985)
∗ Backpropagation (Rumelhart, Hinton, Williams; 1986)
∗ ART-networks (Carpenter, Grossberg; 1992)
∗ Support Vector Machines

9

Hebb’s Learning Law
∗ In 1949, Donald Hebb formulated William James’
principle of association into a mathematical form.

•
•
•

If the activation of the neurons, y1 and y2 , are
both on (+1) then the weight between the two
neurons grow. (Off: 0)
Else the weight between remains the same.
However, when bipolar activation {-1,+1}
scheme is used, then the weights can also
decrease when the activation of two neurons
does not match.
10

Real Neural Learning
∗ Synapses change size and strength with experience.
∗ Hebbian learning: When two connected neurons are
firing at the same time, the strength of the synapse
between them increases.
∗ “Neurons that fire together, wire together.”

11

Biological Neurons
∗ Human brain = tens of thousands
of neurons
∗ Each neuron is connected to
thousands other neurons
∗ A neuron is made of:
∗ The soma: body of the neuron
∗ Dendrites: filaments that provide
input to the neuron
∗ The axon: sends an output signal
∗ Synapses: connection with other
neurons – releases certain
quantities of chemicals called
neurotransmitters to other
neurons

12

Modeling of Brain Functions

13

The biological neuron
∗ The pulses
generated by
the neuron
travels along
the axon as an
electrical wave.
∗ Once these
pulses reach the
synapses at the
end of the axon
open up
chemical
vesicles exciting
the other
neuron.
14

How do NNs and ANNs work?
∗ Information is transmitted as a series of
electric impulses, so-called spikes.
∗ The frequency and phase of these spikes
encodes the information.
∗ In biological systems, one neuron can be
connected to as many as 10,000 other
neurons.
∗ Usually, a neuron receives its information
from other neurons in a confined area
15

Navigation of a car
∗ Done by Pomerlau. The network takes inputs from a 34X36 video image
and a 7X36 range finder. Output units represent “drive straight”, “turn
left” or “turn right”. After training about 40 times on 1200 road images,
the car drove around CMU campus at 5 km/h (using a small workstation
on the car). This was almost twice the speed of any other non-NN
algorithm at the time.

16

Automated driving at 70 mph on a
public highway
Camera
image
30 outputs
for steering

30x32 weights
into one out of
four hidden
unit

4 hidden
units
30x32 pixels
as inputs

17

Computers vs. Neural Networks
“Standard” Computers

Neural Networks

one CPU

highly parallel
processing

fast processing units
units

slow processing

reliable units

unreliable units

static infrastructure
infrastructure

dynamic

18

Neural Network Application

•Pattern recognition can be implemented using NN
•The figure can be T or H character, the network should
identify each class of T or H.

Soft Computering Technics - Unit2

Simple Neuron
X1

Inputs

X2

Output

Xn

b

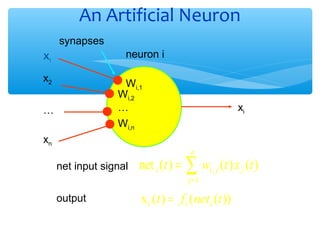
An Artificial Neuron
synapses

x1

neuron i

x2

Wi,1
Wi,2
…
Wi,n

…

xi

xn
net input signal
output

net i (t ) =

n

∑w
j =1

i, j

(t ) x j (t )

x i (t ) = f i (neti (t ))

Neural Network

Input Layer

Hidden 1

Hidden 2

Output Layer

Network Layers
The common type of ANN consists of three layers of
neurons: a layer of input neurons connected to the layer
of hidden neuron which is connected to a layer of output
neurons.

Architecture of ANN
∗ Feed-Forward networks
Allow the signals to travel one way from input to output
∗ Feed-Back Networks
The signals travel as loops in the network, the output is
connected to the input of the network

How do NNs and ANNs Learn?
∗ NNs are able to learn by adapting their connectivity
patterns so that the organism improves its behavior
in terms of reaching certain (evolutionary) goals.
∗ The NN achieves learning by appropriately adapting
the states of its synapses.

Learning Rule

∗ The learning rule modifies the weights of the
connections.
∗ The learning process is divided into Supervised and
Unsupervised learning

Supervised Network

∗ Which means there exists an external teacher. The
target is to minimization of the error between the
desired and computed output

Unsupervised Network
Uses no external teacher and is based upon only local
information.

Perceptron
∗ It is a network of one neuron and hard limit transfer
function
X1
W1
Inputs

X2

W2

Wn
Xn

∑

f

Output

Perceptron
∗ The perceptron is given first a randomly weights vectors
∗ Perceptron is given chosen data pairs (input and desired
output)
∗ Preceptron learning rule changes the weights according
to the error in output

Perceptron Learning Rule
W new = W old + (t-a) X
Where W new is the new weight
W old is the old value of weight
X is the input value
t is the desired value of output
a is the actual value of output

Example
∗ Let
∗
∗
∗
∗

X1 = [0
X2 = [0
X3 = [1
X4 = [1

∗ W = [2

0]
1]
0]
1]

and
and
and
and

2] and b = -3

t =0
t=0
t=0
t=1

AND Network
∗ This example means we construct a network for AND
operation. The network draw a line to separate the
classes which is called
Classification

Perceptron Geometric View
The equation below describes a (hyper-)plane in the input space
consisting of real valued m-dimensional vectors. The plane
splits the input space into two regions, each of them
describing one class.

m

∑wx
i =1

i i

x2

+ w 0 = 0 decision

decision
region for C1
w1x1 + w2x2 + w0 >= 0

C1

boundary

C2

x1
w1x1 + w2x2 + w0 = 0

Problems
∗ Four one-dimensional data belonging to two classes
are
X = [1 -0.5 3
-2]
T = [1 -1
1
-1]
W = [-2.5
1.75]

Boolean Functions
∗
∗
∗
∗

Take in two inputs (-1 or +1)
Produce one output (-1 or +1)
In other contexts, use 0 and 1
Example: AND function

∗ Produces +1 only if both inputs are +1

∗ Example: OR function

∗ Produces +1 if either inputs are +1

∗ Related to the logical connectives from F.O.L.

The First Neural Neural Networks
X1

1
Y

X2

1

AND Function

Threshold(Y) = 2

AND
X1
1
1
0
0

X2
1
0
1
0

Y
1
0
0
0

Simple Networks

-1
x
y

W = 1.5
t = 0.0
W=1

Exercises
∗ Design a neural network to recognize the problem of
∗ X1=[2
2] , t1=0
∗ X=[1 -2], t2=1
∗ X3=[-2
2], t3=0
∗ X4=[-1
1], t4=1
Start with initial weights w=[0 0] and bias =0

Perceptron: Limitations
 The perceptron can only model linearly separable
classes, like (those described by) the following
Boolean functions:
 AND
 OR
 COMPLEMENT
 It cannot model the XOR.
XOR
 You can experiment with these functions in the
Matlab practical lessons.

Types of decision regions
1

w0 + w1 x1 + w2 x2 > 0

Network
with a single
node

w0

x1 w1

w0 + w1 x1 + w2 x2 < 0

L1

L2

w2

1

1
1

Convex
region
L3

x2

x1
L4
x2

1
-3.5

1
1

One-hidden layer
network that realizes
the convex region

Gaussian Neurons
Another type of neurons overcomes this problem by
using a Gaussian activation function:

f i (net i (t )) = e
fi(neti(t))

net i ( t ) − 1

σ

2

1

0
-1

1

neti(t)

Gaussian Neurons
Gaussian neurons are able to realize non-linear
functions.
Therefore, networks of Gaussian units are in
principle unrestricted with regard to the
functions that they can realize.
The drawback of Gaussian neurons is that we
have to make sure that their net input does
not exceed 1.
This adds some difficulty to the learning in
Gaussian networks.
57

Sigmoidal Neurons
Sigmoidal neurons accept any vectors of real
numbers as input, and they output a real
number between 0 and 1.
Sigmoidal neurons are the most common type
of artificial neuron, especially in learning
networks.
A network of sigmoidal units with m input
neurons and n output neurons realizes a
network function
f: Rm → (0,1)n
58

Sigmoidal Neurons
1

f i (net i (t )) =
fi(neti(t))

1 + e − ( net i (t )− θ ) /τ

1

=
1
0
-1

1

neti(t)

The parameter τ controls the slope of the sigmoid function, while
the parameter θ controls the horizontal offset of the function in a
way similar to the threshold neurons.
59

Sigmoidal Neurons
This leads to a simplified form of the sigmoid function:

1
S (net ) =
1 + e ( − net )
We do not need a modifiable threshold θ, because we will use
“dummy” inputs as we did for perceptrons.
The choice τ = 1 works well in most situations and results in a very
simple derivative of S(net).

60

Sigmoidal Neurons
1
S ( x) =
−x
1+ e
dS ( x)
e− x
S ' ( x) =
=
dx
(1 + e − x ) 2
1 + e− x − 1
1
1
=
=
−
−x 2
−x
(1 + e )
1+ e
(1 + e − x ) 2

= S ( x)(1 − S ( x))
This result will be very useful when we develop the
backpropagation algorithm.
61

Multi-layers Network
∗ Let the network of 3 layers
∗ Input layer
∗ Hidden layer
∗ Output layer

∗ Each layer has different number of neurons
∗ The famous example to need the multi-layer network
is XOR unction

Learning rule
∗ The perceptron learning rule can not be applied to
multi-layer network
∗ We use BackPropagation Algorithm in learning
process

Feed-forward +
Backpropagation

∗ Feed-forward:

∗ input from the features is fed forward in the network from
input layer towards the output layer

∗ Backpropagation:
∗ Method to asses the blame of errors to weights
∗ error rate flows backwards from the output layer to the input
layer (to adjust the weight in order to minimize the output
error)
68

Backprop
∗ Back-propagation training algorithm illustrated:
Network activation
Error computation
Forward Step
Error propagation
Backward Step

∗ Backprop adjusts the weights of the NN in order to
minimize the network total mean squared error.

Correlation Learning
Hebbian Learning (1949):
“When an axon of cell A is near enough to excite a cell B
and repeatedly or persistently takes place in firing it,
some growth process or metabolic change takes place in
one or both cells such that A’s efficiency, as one of the
cells firing B, is increased.”
Weight modification rule:
∆wi,j = c⋅xi⋅xj
Eventually, the connection strength will reflect the
correlation between the neurons’ outputs.

Competitive Learning
• Nodes compete for inputs
• Node with highest activation is the winner
• Winner neuron adapts its tuning (pattern of
weights) even further towards the current
input
• Individual nodes specialize to win
competition for a set of similar inputs
• Process leads to most efficient neural
representation of input space
• Typical for unsupervised learning
71

Backpropagation Learning
Similar to the Adaline, the goal of the Backpropagation
learning algorithm is to modify the network’s weights so
that its output vector
op = (op,1, op,2, …, op,K)
is as close as possible to the desired output vector
dp = (dp,1, dp,2, …, dp,K)
for K output neurons and input patterns p = 1, …, P.
The set of input-output pairs (exemplars)
{(xp, dp) | p = 1, …, P} constitutes the training set.
72

Bp Algorithm
∗ The weight change rule is
ω ij = ω ij + α .error. f
new

old

' (inputi )

∗ Where α is the learning factor <1
∗ Error is the error between actual and trained value
∗ f’ is is the derivative of sigmoid function = f(1-f)

Delta Rule
∗ Each observation contributes a variable amount
to the output
∗ The scale of the contribution depends on the
input
∗ Output errors can be blamed on the weights
∗ A least mean square (LSM) error function can be
defined (ideally it should be zero)
E = ½ (t – y)2

Example
∗ For the network with one neuron in input
layer and one neuron in hidden layer the
following values are given
X=1, w1 =1, b1=-2, w2=1, b2 =1, α=1 and t=1
Where X is the input value
W1 is the weight connect input to hidden
W2 is the weight connect hidden to output
B1 and b2 are bias
T is the training value

Exercises
∗ Perform one iteration of backprpgation to network of
two layers. First layer has one neuron with weight 1
and bias –2. The transfer function in first layer is f=n2
∗ The second layer has only one neuron with weight 1
and bias 1. The f in second layer is 1/n.
∗ The input to the network is x=1 and t=1

Neural Network
Construct a neural network to solve the problem
X1

X2

Output

1.0

1.0

1

9.4

6.4

-1

2.5

2.1

1

8.0

7.7

-1

0.5

2.2

1

7.9

8.4

-1

7.0

7.0

-1

2.8

0.8

1

1.2

3.0

1

7.8

6.1

-1

Initialize the
weights 0.75 , 0.5,
and –0.6

Neural Network
Construct a neural network to solve the XOR problem
X1

X2

Output

1

1

0

0

0

0

1

0

1

0

1

1

Initialize the weights –7.0 , -7.0, -5.0 and –4.0

-0.5
The transfer function is linear
function.
-2

1

1
1

-1
-1

1

3

0.5
-0.5

Consider a transfer function as f(n) = n2. Perform
one iteration of BackPropagation with a= 0.9 for
neural network of two neurons in input layer
and one neuron in output layer. The input values
are X=[1 -1] and t = 8, the weight values between
input and hidden layer are w11 = 1, w12 = - 2, w21
= 0.2, and w22 = 0.1. The weight between input
and output layers are w1 = 2 and w2= -2. The bias
in input layers are b1 = -1, and b2= 3.
W11

X1

W1

W12

X2

W21

W22

W2

Some variations
∗ True gradient descent assumes infinitesmall learning rate
(η). If η is too small then learning is very slow. If large,
then the system's learning may never converge.
∗ Some of the possible solutions to this problem are:
∗ Add a momentum term to allow a large learning rate.
∗ Use a different activation function
∗ Use a different error function
∗ Use an adaptive learning rate
∗ Use a good weight initialization procedure.
∗ Use a different minimization procedure
82

Problems with Local Minima
∗ Backpropagation is gradient descent search

∗ Where the height of the hills is determined by error
∗ But there are many dimensions to the space
∗ One for each weight in the network

∗ Therefore backpropagation

∗ Can find its ways into local minima

∗ One partial solution:

∗ Random re-start: learn lots of networks
∗ Starting with different random weight settings

∗ Can take best network
∗ Or can set up a “committee” of networks to categorise examples

∗ Another partial solution: Momentum

Adding Momentum
∗ Imagine rolling a ball down a hill

Gets stuck
here

Without Momentum

With Momentum

Momentum in Backpropagation
∗ For each weight
∗ Remember what was added in the previous epoch

∗ In the current epoch
∗ Add on a small amount of the previous Δ

∗ The amount is determined by
∗ The momentum parameter, denoted α
∗ α is taken to be between 0 and 1

How Momentum Works
∗ If direction of the weight doesn’t change
∗ Then the movement of search gets bigger
∗ The amount of additional extra is compounded in each
epoch
∗ May mean that narrow local minima are avoided
∗ May also mean that the convergence rate speeds up
∗ Caution:
∗ May not have enough momentum to get out of local
minima
∗ Also, too much momentum might carry search
∗ Back out of the global minimum, into a local minimum

Momentum
∗ Weight update becomes:
∆ wij (n+1) = η (δpj opi) + α ∆ wij(n)
∗ The momentum parameter α is chosen between 0
and 1, typically 0.9. This allows one to use higher
learning rates. The momentum term filters out high
frequency oscillations on the error surface.
What would the learning rate be in a deep valley?

87

Problems with Overfitting
∗ Plot training example error versus test example error:

∗ Test set error is increasing!
∗ Network is overfitting the data
∗ Learning idiosyncrasies in data, not general principles

Avoiding Overfitting
∗ Bad idea to use training set accuracy to terminate
∗ One alternative: Use a validation set
∗ Hold back some of the training set during training
∗ Like a miniature test set (not used to train weights
at all)
∗ If the validation set error stops decreasing, but the
training set error continues decreasing
∗ Then it’s likely that overfitting has started to occur, so stop

∗ Another alternative: use a weight decay factor
∗ Take a small amount off every weight after each
epoch
∗ Networks with smaller weights aren’t as highly fine
tuned (overfit)

Soft Computering Technics - Unit2

More Related Content

What's hot (20)

Similar to Soft Computering Technics - Unit2 (20)

Recently uploaded (20)

Soft Computering Technics - Unit2