Ad
More Related Content
What's hot (20)
Similar to Statistical inference: Estimation (20)
Ad
More from Parag Shah (17)
Ad
Recently uploaded (20)
Statistical inference: Estimation
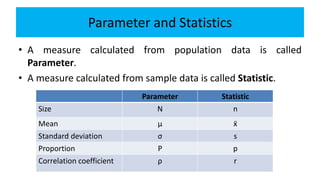
- 2. Parameter and Statistics • A measure calculated from population data is called Parameter. • A measure calculated from sample data is called Statistic. Parameter Statistic Size N n Mean μ x̄ Standard deviation σ s Proportion P p Correlation coefficient ρ r
- 3. Statistical Inference The method to infer about population on the basis of sample information is known as Statistical inference. It mainly consists of two parts: • Estimation • Testing of Hypothesis
- 4. Estimation Estimation is a process whereby we select a random sample from a population and use a sample statistic to estimate a population parameter. There are two ways for estimation: • Point Estimation • Interval Estimation
- 5. Point Estimate Point Estimate – A sample statistic used to estimate the exact value of a population parameter. • A point estimate is a single value and has the advantage of being very precise but there is no information about its reliability. • The probability that a single sample statistic actually equal to the parameter value is extremely small. For this reason point estimation is rarely used.
- 6. Good Estimator Properties of good estimator: 1. Unbiasedness 2. Consistency 3. Sufficiency 4. Efficiency
- 7. Unbiasedness Any sample statistic is said to be an unbiased estimator for the population parameter if on an average the value sample statistic is equal to the parameter value. e.g. 𝐸 𝑥 = 𝜇 i.e. sample mean is an unbiased estimator of population mean
- 8. Consistency An estimator is said to be a consistent estimator for the parameter if the value of statistics gets closer to the value of the parameter and the respective variance of statistics get closer to zero as sample size increases. e.g. 𝐸 𝑥 → 𝜇 and 𝑉 𝑥 = 𝜎2 𝑛 → 0 as sample size n increases
- 9. Sufficiency If a statistic contain almost all information regarding the population parameter that is contained in the population then the statistic is called sufficient estimator for the parameter.
- 10. Efficiency An estimator is said to be an efficient estimator if it contains smaller variance among all variances of all other estimators.
- 11. Interval Estimate Confidence interval (interval estimate) – A range of values defined by the confidence level within which the population parameter is estimated to fall. • The interval estimate is less precise, but gives more confidence.
- 12. Example of Point and Interval Estimate Government wants to know the percentage of cigarette smokers among college students. If we say that there was 10% are smokers, it is a point estimate. But if we make a statement that 8% to 12% of college students are smokers, it is interval estimate.
- 13. Sampling distribution From a population of size N, number of samples of size n can be selected and these samples give different values of a statistics. These different values of statistic can be arranged in form of a frequency distribution which is known as sampling distribution of that statistics. We can have sampling distribution of sample mean, sampling distribution of sample proportion etc.
- 14. Standard Error of a statistics The standard deviation calculated from the observations of a sampling distribution of a statistics is called Standard Error of that statistics. E.g. The standard deviation calculated from the observations of sampling distribution of x̄ is called standard error of x̄. It is denoted by S.E.(x̄)
- 15. Standard Error for Mean when population standard deviation (𝜎) is known S.E.( 𝑥 ) = 𝜎 𝑛 for infinite population S.E.( 𝑥 ) = 𝜎 𝑛 ∗ 𝑁−𝑛 𝑁−1 for finite population
- 16. Standard Error for Mean when population standard deviation (𝜎) is unknown When sample size is large ( n > 30) S.E.( 𝑥 ) = 𝑠 𝑛 for infinite population S.E.( 𝑥 ) = 𝑠 𝑛 ∗ 𝑁− 𝑛 𝑁−1 for finite population When sample size is small ( n ≤ 30) S.E.( 𝑥 ) = 𝑠 𝑛−1 for infinite population S.E.( 𝑥 ) = 𝑠 𝑛−1 ∗ 𝑁− 𝑛 𝑁−1 for finite population
- 17. Standard Error for difference between two means when population standard deviation (𝜎) is known S.E.(𝑥1 − 𝑥2) = 𝜎1 2 𝑛1 + 𝜎2 2 𝑛2
- 18. Standard Error for difference between two means when population standard deviation (𝜎) is unknown When sample size is large ( n > 30) S.E.(𝑥1 − 𝑥2) = 𝑠1 2 𝑛1 + 𝑠2 2 𝑛2 When sample size is small ( n ≤ 30) S.E.(𝑥1 − 𝑥2) = 𝑠2( 1 𝑛1 + 1 𝑛2 ) Where 𝑠2 = 𝑛1∗𝑠1 2+𝑛2∗𝑠2 2 𝑛1+𝑛2−2
- 19. Standard Error for Proportion S.E. (𝑝) = 𝑃𝑄 𝑛 for infinite population S.E. (𝑝) = 𝑃𝑄 𝑛 𝑁−𝑛 𝑁−1 for finite population When population proportion (𝑃) is unknown, then it is estimated by sample proportion (𝑝)
- 20. Standard Error for difference between two proportions Population proportions are known S.E.(𝑝1 − 𝑝2) = 𝑃1 𝑄1 𝑛1 + 𝑃2 𝑄2 𝑛2 Population proportions are unknown S.E.(𝑝1 − 𝑝2) = 𝑃 ∗ 𝑄 ( 1 𝑛1 + 1 𝑛2 ) where 𝑃 = 𝑛1 𝑝1 + 𝑛2 𝑝2 𝑛1 + 𝑛2
- 21. Interval Estimation Confidence Interval has the form: Point estimate ± Margin of error Where Margin of error = Critical value of estimate * Standard Error of estimate
- 22. z table value 1 % 5% 10% Two tailed test (≠ ) 2.58 1.96 1.645 One tailed test ( > or < ) 2.33 1.645 1.28
- 24. C.I. for Population mean (i) When Population standard deviation is known or the sample size is large 𝑥 ± 𝑍 𝛼 × S.E.( 𝑥 ) (ii) When Population standard deviation is unknown and the sample size is small 𝑥 ± 𝑡 𝛼,𝑛−1 × S.E.( 𝑥 )
- 25. Case Study 1 A government agency was charged by the legislature with estimating the length of time it takes citizens to fill out various forms. Two hundred randomly selected adults were timed as they filled out a particular form. The times required had mean 12.8 minutes with standard deviation 1.7 minutes. Construct a 90% confidence interval for the mean time taken for all adults to fill out this form.
- 26. Case Study 2 A thread manufacturer tests a sample of eight lengths of a certain type of thread made of blended materials and obtains a mean tensile strength of 8.2 lb with standard deviation 0.06 lb. Assuming tensile strengths are normally distributed, construct a 90% confidence interval for the mean tensile strength of this thread.
- 27. C.I. for difference between two means (i) When Population standard deviation is known or the sample size is large (𝑥1 − 𝑥2) ± 𝑍 𝛼 × S.E.(𝑥1 − 𝑥2) (ii) When Population standard deviation is unknown and the sample size is small (𝑥1 − 𝑥2) ± 𝑡 𝛼,𝑛1+𝑛2−2 × S.E.(𝑥1 − 𝑥2)
- 28. Case Study 1 Records of 40 used passenger cars and 40 used pickup trucks (none used commercially) were randomly selected to investigate whether there was any difference in the mean time in years that they were kept by the original owner before being sold. For cars the mean was 5.3 years with standard deviation 2.2 years. For pickup trucks the mean was 7.1 years with standard deviation 3.0 years. Construct the 95% confidence interval for the difference in the means based on these data.
- 29. Case Study 2 A university administrator wishes to know if there is a difference in average starting salary for graduates with master’s degrees in engineering and those with master’s degrees in business. Fifteen recent graduates with master’s degree in engineering and 11 with master’s degrees in business are surveyed and the results are summarized below. Construct the 99% confidence interval for the difference in the population means based on these data. n Mean Std. dev Engineering 15 68,535 1627 Business 11 63,230 2033
- 30. C.I. for Population proportion 𝑝 ± 𝑍 𝛼 × S.E.(𝑝)
- 31. Case Study In a random sample of 2,300 mortgages taken out in a certain region last year, 187 were adjustable-rate mortgages. Assuming that the sample is sufficiently large, construct a 99% confidence interval for the proportion of all mortgages taken out in this region last year that were adjustable-rate mortgages.
- 32. C.I. for difference between two proportions (𝑝1 − 𝑝2) ± 𝑍 𝛼 × S.E.(𝑝1 − 𝑝2)
- 33. Case Study A survey for anemia prevalence among women in developing countries was conducted among African and Asian women. Out of 2100 African women, 840 were anemia and out of 1900 Asian women, 323 were anemia. Find a 95% confidence interval for the difference in proportions of all African women with anemia and all women from the Asian with anemia.