Theory of Automata and formal languages unit 2

THEORY OF AUTOMATAAND
FORMAL LANGUAGES
UNIT-2
ABHIMANYU MISHRA
ASSISTANT PROF.(CSE)
JETGI
Abhimanyu Mishra(CSE) JETGI12/31/2016 1

A regular expression (sometimes called a rational expression)is,
in computer science and formal languages theory, a sequence
of characters that define a search pattern. usually this pattern is then used
by in string searching algorithm "find" or "find and replace" operations on
strings.
2. REGULAR EXPRESSION AND LANGUAGES
Abhimanyu Mishra(CSE) JETGI12/31/2016 2

2.1 Definition of Regular Expression:
The set of regular expression of defined by the following rules:
(i) Every letter of ∑ can be made into regular expression, null string,€ itself is
a regular expression.
(ii) If r1 and r2 are regular expression, then
(a) (r1) (b) r1r2
(c) r1+r2 (d) r1
*
(e) r1
+ are also regular expression
(iii) Nothing else is regular expression.
12/31/2016 Abhimanyu Mishra(CSE) JETGI 3

2.1.1 Building Regular Expression
(i) The constants ϵ(null string) and ɸ(empty set) are regular expression,
denote the languages {ϵ} and ɸ, respectively.
That is, L(ϵ) = {ϵ} , and L(ɸ)= ɸ.
(ii) If a is any symbol, then a is regular expression. This expression denotes
the language {a}. That is L(a)={a}.
(iii) A variable, usually capitalized and such as L is a variable, representing
any language.

2.2 Construction of FA for Regular Expression
• The Expression is r+s for some smaller expression r and s. The following
automation serves, where R is automation for r and S is automation for s.
That is, starting at the new start state, We can go to the start state of either
the automation for r or the automation for S
So L(r) and L(s)
ϵ ϵ
Start
ϵ ϵ
R
S

2.The expression rs for some smaller expression r and s. The
automation for the concatenation is ………….
Start ϵ ϵ ϵ
3. The expression is r* for some smaller expression r. Then we use
automation of ……….
ϵ
Start ϵ ϵ
ϵ
R S
R

Example 1: Find the automation for regular expression a.(a+b)*.b.b
Solution:
The basic regular expression involved are a and b,we start with automation for
a and automation for b. Since brackets are evaluated first.(a+b).
ϵ a ϵ
Start
ϵ ϵ
b

Step 2: Since closure is required to take next, we construct automation for (a+b)*
using automation for (a+b) ……..
ϵ
a
ϵ ϵ
Start ϵ ϵ
ϵ b ϵ
ϵ

Step 3: Next we construct the automation for a.(a+b)* as………
ϵ a ϵ ϵ
Star a ϵ ϵ
ϵ b ϵ ϵ

Step 4: Next we construct the automation for a.(a+b)*.b by using automation
ϵ ϵ a ϵ
Start a ϵ ϵ b
ϵ b ϵ
ϵ

Step 5: Now finally we can construct automation for a.(a+b)*.b.b
ϵ ϵ a ϵ
Start a ϵ b b
ϵ ϵ
ϵ b ϵ

Arden's Theorem
In order to find out a regular expression of a Finite Automaton, we use Arden’s
Theorem along with the properties of regular expressions.
Statement −
• Let P and Q be two regular expressions.
• If P does not contain null string
(I) R = Q + RP has a unique solution,
(ii) R = QP*

Proof −
R = Q + (Q + RP)P [After putting the value R = Q + RP]
= Q + QP + RPP
When we put the value of R recursively again and again, we get the following
equation −
R = Q + QP + QP2 + QP3…..
R = Q (ϵ + P + P2 + P3 + …. )
R = QP* [As P* represents (ϵ + P + P2 + P3 + ….) ]
proved.

Assumptions for Applying Arden’s Theorem −
The transition diagram must not have NULL transitions
It must have only one initial state:
Method
Step 1 − Create equations as the following form for all the states of the DFA
having n states with initial state q1.
q1 = q1R11 + q2R21 + … + qnRn1 + ϵ
q2 = q1R12 + q2R22 + … + qnRn2
…………………………………………………………….
…………………………………………………………….
qn = q1R1n + q2R2n + … + qnRnn
Rij represents the set of labels of edges from qi to qj, if no such edge exists,
then Rij = ɸ
Step 2 − Solve these equations to get the equation for the final state in terms of
Rij

Example 1: Construct a regular expression corresponding to the
automata given below −
b
a
b
b a
a
q2
q1
q3

Solution:
Here the initial state is q2 and the final state is q1.
The equations for the three states q1, q2, q3
q1 = q1a + q3a + ϵ (ϵ move is because q1 is the initial state)
q2 = q1b + q2b + q3b
q3 = q2a
Now, we will solve these three equations −
q2 = q1b + q2b + q3b
= q1b + q2b + (q2a)b (Substituting value of q3)
= q1b + q2(b + ab)
= q1b (b + ab)* (Applying Arden’s Theorem)

q1 = q1a + q3a + ϵ
= q1a + q2aa + ϵ (Substituting value of q3)
= q1a + q1b(b + ab*)aa + ϵ (Substituting value of q2)
= q1(a + b(b + ab)*aa) + ϵ
= ϵ (a+ b(b + ab)*aa)*
= (a + b(b + ab)*aa)*
Hence, the regular expression is (a + b(b + ab)*aa)*.

Solve This Problem? Construct the regular expression
0 0,1
1 1
0
q1
q2
q3

Construction of an FA from an RE
We can use Thompson's Construction to find out a Finite Automaton from a
Regular Expression. We will moderate the regular expression into minimum
regular expressions and converting these to NFA and finally to DFA.
Case 1 − For a regular expression ‘a’, we can construct the following FA
Finite Automata for RE = a
Start a
q1 qf

Case 2 − For a regular expression ‘ab’, we can construct the following FA −
Start a b
Case 3 − For a regular expression (a+b), we can construct the following FA −
Start a
b
Case 4 − For a regular expression (a+b)*, we can construct the following FA −
a,b
Start
qfq1 q2
q1 qf
qf

Example:-Convert the following RE into its equivalent DFA − 1 (0 + 1)* 0
0,1
start 1 ϵ ϵ 0
q0 q1 q2 q3 qf

Pumping Lemma for Regular Languages
Theorem
Let L be a regular language. Then there exists a constant ‘c’ such that
for every string w in L −
|w| ≥ c
We can break w into three strings, w = xyz, such that −
|y| > 0
|xy| ≤ c
For all k ≥ 0, the string xykz is also in L.

Applications of Pumping Lemma
Pumping Lemma is to be applied to show that certain languages are not
regular. It should never be used to show a language is regular.
If L is regular, it satisfies Pumping Lemma.
If L is non-regular, it does not satisfy Pumping Lemma.
Method to prove that a language L is not regular
At first, we have to assume that L is regular.
So, the pumping lemma should hold for L.
Use the pumping lemma to obtain a contradiction −

Use the pumping lemma to obtain a contradiction −
Select w such that |w| ≥ c
Select y such that |y| ≥ 1
Select x such that |xy| ≤ c
Assign the remaining string to z.
Select k such that the resulting string is not in L.
Hence L is not regular.

Application of the Pumping Lemma
(i) Select the language L ,You wish to prove non-regular.
(ii) The “adversary” pinks n, the constant mentioned in the pumping lemma,
Once the adversary has picked n, he may not change it.
(iii) Select a string z in L. Your choice may depend implicitly on the of n
chosen.
(iv) The adversary breaks z into u, v and w, subject to the constants that
|uv|<=n and |v|>=1
(v) You achieve a contradiction to the pumping leema by showing, for any
u,v and determined by the adversary that there exit i for which uviw is not
in L.it May then concluded and L is not regular. Your selection of
pumping leema on n,u,v and w.

Example: Prove that language L =(anbn for n= 0,1,2,3……} is not regular
Solution:
Case 1 If middle part y is made off entirely of a’s,as
x aaaaaaa….z
If we jump it as xyyz,xyyyz,then number of a”s increases,but in language {(anbn for n=
0,1,2,3,……} a’s and b’s are equal so it os not allowed.
Case 2 If middle part y is made off entirely of b’s as
x bbbbbbb……z
For the same reason, it is also not allowed.
Case 3 y part is made of some positive number of a’s and some number of b’s. This would
mean that y contain the substring ab
x……aaaaaaaabbbbbbbbbbb…………..z
Then xyyz would have two copies of the substring ab.But every world in L contains
substring ab exactly once.
This proves that the pumping lemma cannot apply to L and therefore L is not regular

Q1.Prove That L={0n1m2n , n,m>=0} is not regular.
Q2. Prove that language L ={0n |n is perfect square} is not regular.
Q3. Prove that language L ={0n |n is perfect cube} is not regular.

AUTOMATA WITH OUTPUT
Here we are using two Machines for finding the Finite Automata Output
(i) Moore Machine
(ii) Mealy Machine

Moore Machine
(i) Moore Machine
Moore machine is an FSM whose outputs depend on only the present
state.
A Moore machine can be described by a 6 tuple (Q, ∑, ∆, δ, ƛ’, q0)
where −
Q is a finite set of states.
∑ is a finite set of symbols called the input alphabet.
∆ is a finite set of symbols called the output alphabet.
δ is the input transition function where δ: Q × Σ → Q
ƛ’ is the output transition function where ƛ’ : Q × Σ → ∆
q0 is the initial state from where any input is processed (q0 ∈ Q).

Representation of Moore Machine:( Transition Table)
Present State Next state at input Output
a=0 a=1
q0 q3 q1 0
q1 q1 q2 1
q2 q2 q3 0
q3 q3 q0 0

Representation of Moore Machine:( Transition Diagram)
0
0
Start 1 1
0
1
0 1 0
0 1 0
q3
q0
q2
q1

Mealy Machine
A Mealy Machine is an FSM whose output depends on the present state as
well as the present input.
It can be described by a 6 tuple (Q, ∑, ∆, δ, ƛ’, q0) where −
Q is a finite set of states.
∑ is a finite set of symbols called the input alphabet.
∆ is a finite set of symbols called the output alphabet.
δ is the input transition function where δ: Q × ∑ → Q
ƛ’ is the output transition function where X: Q → ƛ’,
q0 is the initial state from where any input is processed (q0 ∈ Q).

Representation of Mealy Machine:( Transition Table)
Present State For input a=0 for input a=1
State Output State Output
q1 q3 0 q2 0
q2 q1 1 q4 0
q3 q2 1 q1 1
q4 q4 1 q3 0

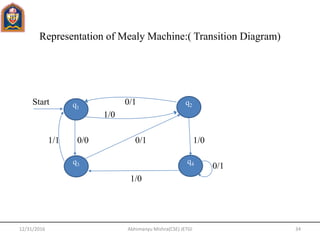
Representation of Mealy Machine:( Transition Diagram)
Start 0/1
1/0
1/1 0/0 0/1 1/0
0/1
1/0
q1
q3 q4
q2

Mealy Machine vs. Moore Machine
Mealy Machine Moore Machine
Output depends both upon present
state and present input.
Output depends only upon the
present state.
Generally, it has fewer states than
Moore Machine.
Generally, it has more states than
Mealy Machine.
Output changes at the clock edges. Input change can cause change in
output change as soon as logic is
done.
Mealy machines react faster to
inputs.
In Moore machines, more logic is
needed to decode the outputs since
it has more circuit delays.

Theory of Automata and formal languages unit 2

More Related Content

What's hot (20)

Viewers also liked (20)

Similar to Theory of Automata and formal languages unit 2 (20)

More from Abhimanyu Mishra (19)

Recently uploaded (20)

Theory of Automata and formal languages unit 2