![An example (Substitution method )
• T(n) = 2T(floor(n/2) ) +n
We guess that the solution is T(n)=0(n lg n).
i.e. to show that T(n) ≤ cn lg n , for some constant c> 0 and n ≥ m.
Assume that this bound holds for [n/2]. So , we get
T(n) ≤ 2(c floor (n/2) lg(floor(n/2))) + n
≤ cn lg(n/2) + n
= cn lg n – cn lg 2 + n
= cn lg n – cn + n
≤ cn lg n
where , the last step holds as long as c≥ 1.](https://image.slidesharecdn.com/timecomplexity-170329135457/85/Time-complexity-9-320.jpg)
Time complexity
- 1. Table Of Contents Solving Recurrences The Master Theorem
- 3. Recurrences • The expression: is a recurrence. – Recurrence: an equation that describes a function in terms of its value on smaller functions >+ = = 1 2 2 1 )( ncn n T nc nT
- 5. Solving Recurrences • Substitution method • Iteration method • Master method
- 6. Solving Recurrences • The substitution method (CLR 4.1) – “Making a good guess” method – Guess the form of the answer, then use induction to find the constants and show that solution works – Examples: • T(n) = 2T(n/2) + Θ(n) T(n) = Θ(n lg n) • T(n) = 2T(n/2) + n ???
- 7. Solving Recurrences • The substitution method (CLR 4.1) – “Making a good guess” method – Guess the form of the answer, then use induction to find the constants and show that solution works – Examples: • T(n) = 2T(n/2) + Θ(n) T(n) = Θ(n lg n) • T(n) = 2T(n/2) + n T(n) = Θ(n lg n) • T(n) = 2T(n/2 )+ 17) + n ???
- 8. Substitution method • Guess the form of the solution . • Use mathematical induction to find the constants and show that the solution works . The substitution method can be used to establish either upper or lower bounds on a recurrence.
- 9. An example (Substitution method ) • T(n) = 2T(floor(n/2) ) +n We guess that the solution is T(n)=0(n lg n). i.e. to show that T(n) ≤ cn lg n , for some constant c> 0 and n ≥ m. Assume that this bound holds for [n/2]. So , we get T(n) ≤ 2(c floor (n/2) lg(floor(n/2))) + n ≤ cn lg(n/2) + n = cn lg n – cn lg 2 + n = cn lg n – cn + n ≤ cn lg n where , the last step holds as long as c≥ 1.
- 10. • Boundary conditions : Suppose , T(1)=1 is the sole boundary condition of the recurrence . then , for n=1 , the bound T(n)≤ c n lg n yields T(1)≤ c lg1=0 , which is at odds with T(1)=1. Thus ,the base case of our inductive proof fails to hold. To overcome this difficulty , we can take advantage of the asymptotic notation which only requires us to prove T(n)≤c n lg n for n≥ m. The idea is to remove the difficult boundary condition T(1)= 1 from consideration. Thus , we can replace T(1) by T(2) as the base cases in the inductive proof , letting m=2.
- 11. Contd.... From the recurrence , with T(1) = 1, we get T(2)=4 We require T(2)≤ c 2 lg 2 It is clear that , any choice of c≥2 suffices for the base cases
- 12. Are we done? • Have we proved the case for n =3. • Have we proved that T(3) ≤ c 3 lg 3. • No. Since floor(3/2) = 1 and for n =1, it does not hold. So induction does not apply on n= 3. • From the recurrence, with T(1) = 1, we get T(3) = 5. The inductive proof that T(n) ≤ c n lg n for some constant c≥1 can now be completed by choosing c large enough that T(3)≤c 3 lg 3 also holds. It is clear that , any choice of c ≥ 2 is sufficient for this to hold. Thus we can conclude that T(n) ≤ c n lg n for any c ≥ 2 and n ≥ 2.
- 13. Solving Recurrences • Another option is “iteration method” – Expand the recurrence – Work some algebra to express as a summation – Evaluate the summation • We will show some examples
- 14. • Solve the following recurrence: T(n) = T(αn) + T(βn) + n, where 0 < α ≤ β < 1 Assume suitable initial conditions. Assignment 4
- 15. Recursive Complexity Patterns • When you have simple recurrence relations of the form • T(n) = T(n-1) + f(n), then you have complexity of O(n*f(n)) • T(n) = T(n/k) + f(n), then you have complexity of O(logk n * f(n))
- 16. • Consider the Fibonacci sequence recursive calculation: • F(1) = 1 F(2) = 1 F(n) = F(n-1)+F(n-2) • Its recurrence relation time is • T(1) = 1 T(2) = 1 T(n) = T(n-1) + T(n-2) + 1 • Solving is a little beyond this course, but T(n) = O(2n ) or "exponential“
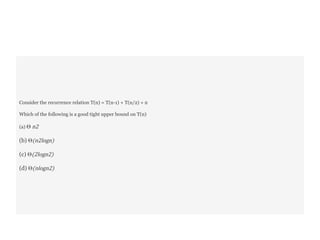
- 17. Consider the recurrence relation T(n) = T(n-1) + T(n/2) + n Which of the following is a good tight upper bound on T(n) (a) Θ n2 (b) Θ(n2logn) (c) Θ(2logn2) (d) Θ(nlogn2)
- 18. • Lets Solve it by substitution. T(n) = T(n-1) + T(n/2) + n = T(n-2) + T(n/4) + (n-1) + n = T(n-3) + T(n/8) + (n-2) + (n-1) + n = T(n-4) + T(n/16) + (n-3) + (n-2) + (n-1) + n = ------------ = ------------ = ------------- = T(n-k) + T(n/(2^k)) + (n-(k-1)) + (n-(k-2)) + ------------------------------ + (n-2) + (n-1) + n Now consider n = 2^k, then k = log n = T((2^k) - k) + T((2^k)/(2^k)) + (n - k + 1) + (n - k + 2) + ---------------------- + (n - 1) + n Now Put value of K = (2^(log n) - log n) + 1 + (n - log n + 1) + (n - log n + 2) + ------------------------ + n Here series {(n - log n + 1) + (n - log n + 2) + ---------------------- + (n - 1) + n} are in AP with (log n) element then Hence Sn = ((log n)/2) *(n -log n + 1 + n) = O(n.log n) Hence, T(n) = 2^(log n) From all the given answer, Option C is asymptotically close to T(n), Hence C will be the answer.
- 19. The Master Theorem • Given: a divide and conquer algorithm – An algorithm that divides the problem of size n into a subproblems, each of size n/b – Let the cost of each stage (i.e., the work to divide the problem + combine solved subproblems) be described by the function f(n) • Then, the Master Theorem gives us a cookbook for the algorithm’s running time:
- 20. The Master Theorem • if T(n) = aT(n/b) + f(n) then ( ) ( ) ( ) ( ) ( ) ( ) < > < Ω= Θ= = Θ Θ Θ = + − 1 0 largefor)()/( AND)( )( )( )( log)( log log log log log c nncfbnaf nnf nnf nOnf nf nn n nT a a a a a b b b b b ε ε ε
- 21. Cont.
- 22. Using The Master Method • T(n) = 9T(n/3) + n – a=9, b=3, f(n) = n – nlogb a = nlog3 9 = Θ(n2 ) – Since f(n) = O(nlog3 9 - ε ), where ε=1, case 1 applies: – Thus the solution is T(n) = Θ(n2 ) ( ) ( )ε− =Θ= aa bb nOnfnnT loglog )(when)(
- 23. More Examples of Master’s Theorem • T(n) = 3T(n/5) + n o/p nlog35 • T(n) = 2T(n/2) + n o/p : nlogn • T(n) = 2T(n/2) + 1 • T(n) = T(n/2) + n • T(n) = T(n/2) + 1
- 24. When Master’s Theorem cannot be applied • T(n) = 2T(n/2) + n logn • T(n) = 2T(n/2) + n/ logn
- 25. Reference • https://en.wikipedia.org/wiki/Master_theorem • http://stackoverflow.com/questions/8185079/how-to-calculate- binary-search-complexity • http://www.csd.uwo.ca/~moreno/CS433- CS9624/Resources/master.pdf • https://en.wikipedia.org/wiki/Time_complexity • http://stackoverflow.com/questions/20512642/big-o-confusion- log2n-vs-log3n