Unit 7 sorting

Sorting
1
By:
Dabal Singh Mahara
2017

Unit – 7 Sorting
Contents Hours Marks
a. Introduction
b. Bubble sort
c. Insertion sort
d. Selection sort
e. Quick sort
f. Merge sort
g. Comparison and efficiency of sorting
5 7
2

 Sorting is among the most basic problems in algorithm design.
 Sorting is important because it is often the first step in more complex
algorithms.
 Sorting is to take an unordered set of comparable items and arrange them
in some order.
 That is, sorting is a process of arranging the items in a list in some order
that is either ascending or descending order.
 Let a[n] be an array of n elements a0,a1,a2,a3........,an-1 in memory. The
sorting of the array a[n] means arranging the content of a[n] in either
increasing or decreasing order.
i.e. a0<=a1<=a2<=a3<.=.......<=an-1
Introduction
3
• Efficient sorting is important for optimizing the use of other algorithms
(such as search and merge algorithms) that require sorted lists to work
correctly.

512354277 101
1 2 3 4 5 6
5 12 35 42 77 101
1 2 3 4 5 6
• Input: A sequence of n numbers a1, a2, . . . , an
• Output: A permutation (reordering) a1’, a2’, . . . , an’ of the input sequence such that
a1’ ≤ a2’ ≤ · · · ≤ an’
The Sorting Problem
4

Terminology
● Internal Sort:
Internal sorting algorithms assume that data is stored in an array in main memory of
computer. These methods are applied to small collection of data. That is, the entire
collection of data to be sorted is small enough that the sorting can take place within
main memory. Examples are: Bubble, Insertion, Selection, Quick, merge etc.
• External Sort:
When collection of records is too large to fit in the main memory, records must reside
in peripheral or external memory. The only practical way to sort it is to read some
records from the disk do some rearranging then write back to disk. This process is
repeated until the file is sorted. The sorting techniques to deal with these problems are
called external sorting. Sorting large collection of records is central to many
applications, such as processing of payrolls and other business databases. . Example:
external merge sort
5

• In-place Sort
The algorithm uses no additional array storage, and hence (other than perhaps the system’s recursion
stack) it is possible to sort very large lists without the need to allocate additional working storage.
Examples are: Bubble sort, Insertion Sort, Selection sort
• Stable Sort:
Sort is said to be stable if elements with equal keys in the input list are kept in the same order in
the output list. If all keys are different then this distinction is not necessary.
But if there are equal keys, then a sorting algorithm is stable if whenever there are two records (let's
say R and S) with the same key, and R appears before S in the original list, then R will always appear
before S in the sorted list.
However, assume that the following pairs of numbers are to be sorted by their first component:
• (4, 2) (3, 7) (3, 1) (5, 6)
• (3, 7) (3, 1) (4, 2) (5, 6) (order maintained)
• (3, 1) (3, 7) (4, 2) (5, 6) (order changed)
• Adaptation to Input:
if the sorting algorithm takes advantage of the sorted or nearly sorted input, then the algorithm is
called adaptive otherwise not. Example: insertion sort is adaptive
6
Terminology

Bubble Sort
• The basic idea of this sort is to pass through the array sequentially several
times.
• Each pass consists of comparing each element in the array with its successor
(for example a[i] with a[i + 1]) and interchanging the two elements if they
are not in the proper order.
• After each pass an element is placed in its proper place and is not considered
in succeeding passes.
7

"Bubbling Up" the Largest Element
• Traverse a collection of elements
– Move from the front to the end
– “Bubble” the largest value to the end using pair-wise
comparisons and swapping
512354277 101
1 2 3 4 5 6
8

– “Bubble” the largest value to the end using pair-wise comparisons
and swapping
512354277 101
1 2 3 4 5 6
Swap42 77
9

and swapping
512357742 101
1 2 3 4 5 6
Swap35 77
10

and swapping
512773542 101
1 2 3 4 5 6
Swap12 77
11

and swapping
577123542 101
1 2 3 4 5 6
No need to swap
12

and swapping
577123542 101
1 2 3 4 5 6
Swap5 101
13

and swapping
77123542 5
1 2 3 4 5 6
101
Largest value correctly placed
14

Items of Interest
• Notice that only the largest value is correctly
placed
• All other values are still out of order
• So we need to repeat this process
77123542 5
1 2 3 4 5 6
101
Largest value correctly placed
15

Repeat “Bubble Up” How Many Times?
• If we have N elements…
• And if each time we bubble an element, we place it in its
correct location…
• Then we repeat the “bubble up” process N – 1 times.
• This guarantees we’ll correctly place all N elements.
16

“Bubbling” All the Elements
77123542 5
1 2 3 4 5 6
101
5421235 77
1 2 3 4 5 6
101
4253512 77
1 2 3 4 5 6
101
4235512 77
1 2 3 4 5 6
101
4235125 77
1 2 3 4 5 6
101
N-1
17

Reducing the Number of Comparisons
12354277 101
1 2 3 4 5 6
5
77123542 5
1 2 3 4 5 6
101
5421235 77
1 2 3 4 5 6
101
4253512 77
1 2 3 4 5 6
101
4235512 77
1 2 3 4 5 6
101
18

Algorithm
BubbleSort(A, n)
{
for(i = 0; i <n-1; i++)
{
for(j = 0; j < n-i-1; j++)
{
if(A[j] > A[j+1])
{
temp = A[j];
A[j] = A[j+1];
A[j+1] = temp;
}
}
}
}
19

Properties:
 Stable
 O(1) extra space
 O(n2) comparisons and swaps
 Adaptive: O(n) when nearly sorted input
Time Complexity:
• Inner loop executes for (n-1) times when i=0, (n-2) times when i=1 and so on:
Time complexity = (n-1) + (n-2) + (n-3) + …………………………. +2 +1
= O(n2)
Space Complexity:
• Since no extra space besides 3 variables is needed for sorting, Space complexity =
O(n)
20

Exercise
• Trace Bubble Sort for the input data:
25, 57, 48, 37, 12, 92, 86, 33
21

Selection Sort
• Idea:
Find the least (or greatest) value in the array, swap it into the leftmost(or
rightmost)component (where it belongs), and then forget the leftmost
component. Do this repeatedly.
• Process:
 Let a[n] be a linear array of n elements. The selection sort works as follows:
 Pass 1: Find the location loc of the maximum element in the list of n
elements a[0], a[1], a[2], a[3], …......,a[n-1] and then interchange a[loc] and
a[n-1].
 Pass 2: Find the location loc of the max element in the sub-list of n-1
elements a[0], a[1], a[2], a[3], …......,a[n-2] and then interchange a[loc] and
a[n-2].
 Continue in the same way. Finally, we will get the sorted list:
a[0]<=a[1]<= a[2]<=a[3]<= .....<= a[n-1]. 22

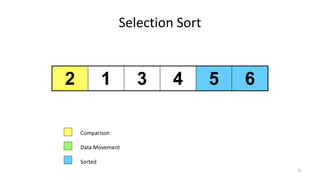
Selection Sort
5 1 3 4 6 2
Comparison
Data Movement
Sorted
23

Selection Sort
5 1 3 4 6 2
Comparison
Data Movement
Sorted
24

Selection Sort
5 1 3 4 6 2
Comparison
Data Movement
Sorted
25

Selection Sort
5 1 3 4 6 2
Comparison
Data Movement
Sorted
26

Selection Sort
5 1 3 4 6 2
Comparison
Data Movement
Sorted
27

Selection Sort
5 1 3 4 6 2
Comparison
Data Movement
Sorted
28

Selection Sort
5 1 3 4 6 2
Comparison
Data Movement
Sorted
29

Selection Sort
5 1 3 4 6 2
Comparison
Data Movement
Sorted

Largest
30

Selection Sort
5 1 3 4 2 6
Comparison
Data Movement
Sorted
31

Selection Sort
5 1 3 4 2 6
Comparison
Data Movement
Sorted
32

Selection Sort
5 1 3 4 2 6
Comparison
Data Movement
Sorted
33

Selection Sort
5 1 3 4 2 6
Comparison
Data Movement
Sorted
34

Selection Sort
5 1 3 4 2 6
Comparison
Data Movement
Sorted
35

Selection Sort
5 1 3 4 2 6
Comparison
Data Movement
Sorted
36

Selection Sort
5 1 3 4 2 6
Comparison
Data Movement
Sorted
37

Selection Sort
5 1 3 4 2 6
Comparison
Data Movement
Sorted

Largest
38

Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted
39

Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted
40

Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted
41

Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted
42

Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted
43

Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted
44

Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted

Largest
45

Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted
46

Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted
47

Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted
48

Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted
49

Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted
50

Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted

Largest
51

Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted
52

Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted
53

Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted
54

Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted
55

Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted

Largest
56

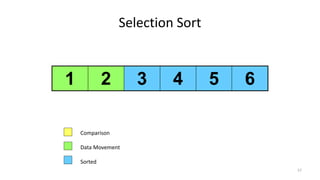
Selection Sort
1 2 3 4 5 6
Comparison
Data Movement
Sorted
57

Selection Sort
1 2 3 4 5 6
Comparison
Data Movement
Sorted
DONE!
58

Algorithm:
SelectionSort(A)
{
for( i = 0; i < n-1 ; i++)
{
max = A[0];
loc=0;
for ( j = 1; j < =n-1-i ; j++)
{
if (A[j] > max)
{
max = A[j];
loc=j;
}
}
if( n-1-i!=loc)
swap(A[n-1-i],A[loc]);
}
}
59

60
Example:
Consider the array: 15, 10, 20, 25, 5
After Pass 1: 15, 10, 20, 5, 25
After Pass 2: 15, 10, 5, 20, 25
After Pass 3: 5, 10, 15, 20, 25
After Pass 4: 5, 10, 15, 20, 25
Time Complexity:
• Inner loop executes for (n-1) times when i=0, (n-2) times when i=1 and so on: Time
complexity = (n-1) + (n-2) + (n-3) + …………………………. +2 +1
= O(n2)
• The complexity of this algorithm is same as that of bubble sort, but number of swap
operations is reduced greatly.
Exchange largest element and
rightmost one

61
Properties:
 Not- stable
 In-place sorting (O(1) extra space)
 Most time depends upon comparisons O(n2) comparisons
 Not adaptive
 Minimum number of swaps, so in the applications where cost of
swapping items is high selection sort is the algorithm of choice.
Space Complexity:
Since no extra space besides 5 variables is needed for
sorting, Space complexity = O(n)

• Idea: Like sorting a hand of playing cards start with an empty left hand and the cards
facing down on the table. Remove one card at a time from the table, Compare it with
each of the cards already in the hand, from right to left and insert it into the correct
position in the left hand. The cards held in the left hand are sorted.
• Suppose an array a[n] with n elements. The insertion sort works as follows:
• Pass 1: a[0] by itself is trivially sorted.
• Pass 2: a[1] is inserted either before or after a[0] so that a[0], a[1] is sorted.
• Pass 3: a[2] is inserted into its proper place in a[0],a[1] that is before a[0], between a[0]
and a[1], or after a[1] so that a[0],a[1],a[2] is sorted.
.......................................
• Pass N: a[n-1] is inserted into its proper place in a[0],a[1],a[2],........,a[n-2] so that
a[0],a[1],a[2],............,a[n-1] is sorted with n elements.
62
Insertion Sort

64
InsertionSort(A)
{
for( i = 1;i < n ;i++)
{
temp = A[i]
for ( j = i -1; j >= 0; j--)
{
if(A[j] > temp )
A[j+1] = A[j];
}
A[j+1] = temp;
}
}
Algorithm:

66
• Best case:
If array elements are already sorted, inner loop executes only 1 time for i=1,2,3,… , n-1 for
each. So, total time complexity = 1+1+1+ …………..+1 (n-1) times = n-1 = O(n)
• Space Complexity:
Since no extra space besides 3variables is needed for sorting,
Space complexity = O(n)
Properties:
 Stable Sorting
 In-place sorting (O(1) extra space)
 Most time depends upon comparisons O(n2) comparisons
 Run time depends upon input (O(n) when nearly sorted input)
 O(n2) comparisons and swaps
Complexity

67
• This algorithm is based on the divide and conquer paradigm.
• The main idea behind this sorting is: partitioning of the elements into two
groups and sort these parts recursively. The two partitions contain values that
are either greater or smaller than the key .
• It possesses very good average case complexity among all the sorting
algorithms.
Quick-Sort
Steps for Quick Sort:
• Divide: partition the array into two non-empty sub
arrays.
• Conquer: two sub arrays are sorted recursively.
• Combine: two sub arrays are already sorted in place so
no need to combine

68
Quicksort Algorithm
To sort a[left...right]:
1. if left < right:
1.1. Partition a[left...right] such that: all a[left...p-1] are less
than a[p], and all a[p+1...right] are >= a[p]
1.2. Quicksort a[left...p-1]
1.3. Quicksort a[p+1...right]
2. Terminate
p
numbers less
than p
numbers greater than or
equal to p
p

69
Partitioning in Quicksort
• Choose an array value (say, the first) to use as the pivot
• Starting from the left end, find the first element that is greater
than the pivot
• Searching backward from the right end, find the first element that
is less than or equal to the pivot
• Interchange (swap) these two elements
• Repeat, searching from where we left off, until done

70
Partitioning
To partition a[left...right]:
1. Set pivot = a[left], l = left + 1, r = right;
2. while l < r, do
2.1. while l < right & a[l] <= pivot , set l = l + 1
2.2. while r > left & a[r] > pivot , set r = r - 1
2.3. if l < r, swap a[l] and a[r]
3. Set a[left] = a[r], a[r] = pivot
4. Terminate

71
Algorithm:
QuickSort(A,l,r)
{
if(l<r)
{
p = Partition(A,l,r);
QuickSort(A,l,p-1);
QuickSort(A,p+1,r);
}
}

72
Partition(A,l,r)
{
x =l;
y =r ;
p = A[l];
while(x<y)
{
while(A[x] <= p)
x++;
while(A[y] >p)
y--;
if(x<y)
swap(A[x],A[y]);
}
A[l] = A[y];
A[y] = p;
return y; //return position of pivot
}

73
Example: a[]={5, 3, 2, 6, 4, 1, 3, 7}
(1 3 2 3 4) 5 (6 7)
and continue this process for each sub-arrays and finally we get a sorted array.

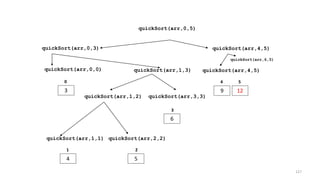
Trace of QuickSort Algorithm
74

6 5 9 12 3 4
0 1 2 3 4 5
quickSort(arr,0,5)
75

quickSort(arr,0,5)
6 5 9 12 3 4
0 1 2 3 4 5
partition(arr,0,5)
76

quickSort(arr,0,5)
6 5 9 12 3 4
0 1 2 3 4 5
partition(arr,0,5)
pivot= ?
Partition Initialization...
77

quickSort(arr,0,5)
6 5 9 12 3 4
0 1 2 3 4 5
partition(arr,0,5)
pivot=6
78

quickSort(arr,0,5)
6 5 9 12 3 4
0 1 2 3 4 5
partition(arr,0,5)
left right
pivot=6
79

quickSort(arr,0,5)
6 5 9 12 3 4
0 1 2 3 4 5
partition(arr,0,5)
left right
pivot=6
right moves to the left until
value that should be to left
of pivot...
80

quickSort(arr,0,5)
6 5 9 12 3 4
0 1 2 3 4 5
partition(arr,0,5)
left right
pivot=6
81

quickSort(arr,0,5)
6 5 9 12 3 4
0 1 2 3 4 5
partition(arr,0,5)
left right
pivot=6
left moves to the right until
value that should be to right
of pivot...
82

quickSort(arr,0,5)
6 5 9 12 3 4
0 1 2 3 4 5
partition(arr,0,5)
left right
pivot=6
83

quickSort(arr,0,5)
6 5 9 12 3 4
0 1 2 3 4 5
partition(arr,0,5)
left right
pivot=6
84

quickSort(arr,0,5)
6 5 4 12 3 9
0 1 2 3 4 5
partition(arr,0,5)
left right
pivot=6
of pivot...
85

quickSort(arr,0,5)
6 5 4 12 3 9
0 1 2 3 4 5
partition(arr,0,5)
left right
pivot=6
86

quickSort(arr,0,5)
6 5 4 12 3 9
0 1 2 3 4 5
partition(arr,0,5)
left right
pivot=6
swap arr[left] and arr[right]
87

quickSort(arr,0,5)
6 5 4 3 12 9
0 1 2 3 4 5
partition(arr,0,5)
left
right
pivot=6
right & left CROSS!!!
88

quickSort(arr,0,5)
6 5 4 3 12 9
0 1 2 3 4 5
partition(arr,0,5)
left
right
pivot=6
1 - Swap pivot and arr[right]
89

quickSort(arr,0,5)
3 5 4 6 12 9
0 1 2 3 4 5
partition(arr,0,5)
left
right
pivot=6
90

quickSort(arr,0,5)
3 5 4 6 12 9
0 1 2 3 4 5
partition(arr,0,5)
left
right
pivot=6
2 - Return new location of pivot to caller
return 3
91

quickSort(arr,0,5) 3 5 4 6 12 9
0 1 2 3 4 5
Recursive calls to quickSort()
using partitioned array...
pivot
position
92

quickSort(arr,0,5)
3 5 4 6 12 9
0 1 2 3 4 5
quickSort(arr,0,3)
3 5 4 6
0 1 2 3
quickSort(arr,4,5)
12 9
4 5
93

quickSort(arr,0,5)
quickSort(arr,0,3)
3 5 4 6
0 1 2 3
quickSort(arr,4,5)
12 9
4 5
partition(arr,0,3)
94

quickSort(arr,0,3)
3 5 4 6
0 1 2 3
quickSort(arr,4,5)
12 9
4 5
partition(arr,0,3)
quickSort(arr,0,5)
95

quickSort(arr,0,3)
3 5 4 6
0 1 2 3
quickSort(arr,4,5)
12 9
4 5
partition(arr,0,3)
quickSort(arr,0,5)
96

quickSort(arr,0,3)
3 5 4 6
0 1 2 3
quickSort(arr,4,5)
12 9
4 5
partition(arr,0,3)
left
quickSort(arr,0,5)
97

quickSort(arr,0,3)
3 5 4 6
0 1 2 3
quickSort(arr,4,5)
12 9
4 5
partition(arr,0,3)
left right
quickSort(arr,0,5)
98

of pivot...
quickSort(arr,0,3)
3 5 4 6
0 1 2 3
quickSort(arr,4,5)
12 9
4 5
partition(arr,0,3)
left right
quickSort(arr,0,5)
99

quickSort(arr,0,3)
3 5 4 6
0 1 2 3
quickSort(arr,4,5)
12 9
4 5
partition(arr,0,3)
left right
quickSort(arr,0,5)
100

quickSort(arr,0,3)
3 5 4 6
0 1 2 3
quickSort(arr,4,5)
12 9
4 5
partition(arr,0,3)
left right
quickSort(arr,0,5)
101

quickSort(arr,0,3)
3 5 4 6
0 1 2 3
quickSort(arr,4,5)
12 9
4 5
partition(arr,0,3)
left
right
quickSort(arr,0,5)
102

quickSort(arr,0,3)
3 5 4 6
0 1 2 3
quickSort(arr,4,5)
12 9
4 5
partition(arr,0,3)
left
right
quickSort(arr,0,5)
103

quickSort(arr,0,3)
3 5 4 6
0 1 2 3
quickSort(arr,4,5)
12 9
4 5
partition(arr,0,3)
left
right
quickSort(arr,0,5)
104

quickSort(arr,0,3)
3 5 4 6
0 1 2 3
quickSort(arr,4,5)
12 9
4 5
partition(arr,0,3)
left
right
2 - Return new location of pivot to caller
return 0
quickSort(arr,0,5)
105

quickSort(arr,0,3)
3 5 4 6
0 1 2 3
quickSort(arr,4,5)
12 9
4 5
quickSort(arr,0,5)
Recursive calls to quickSort()
using partitioned array...
106

quickSort(arr,0,3) quickSort(arr,4,5)
12 9
4 5
quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
5 4 6
1 2 3
107

12 9
4 5
quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
5 4 6
1 2 3
Base case triggered...
halting recursion.
108

12 9
4 5
quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
5 4 6
1 2 3
Base Case: Return
109

12 9
4 5
quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
5 4 6
1 2 3
partition(arr,1,3)
110

12 9
4 5
quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
5 4 6
1 2 3
partition(arr,1,3)
111

12 9
4 5
quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
5 4 6
1 2 3
partition(arr,1,3)
left
112

12 9
4 5
quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
5 4 6
1 2 3
partition(arr,1,3)
left right
of pivot...
113

12 9
4 5
quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
5 4 6
1 2 3
partition(arr,1,3)
left right
114

12 9
4 5
quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
5 4 6
1 2 3
partition(arr,1,3)
left right
of pivot...
115

12 9
4 5
quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
5 4 6
1 2 3
partition(arr,1,3)
left
right
116

12 9
4 5
quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
5 4 6
1 2 3
partition(arr,1,3)
left
right
right & left CROSS!
117

12 9
4 5
quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
5 4 6
1 2 3
partition(arr,1,3)
left
right
right & left CROSS!
1- swap pivot and arr[right]
118

12 9
4 5
quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
4 5 6
1 2 3
partition(arr,1,3)
left
right
right & left CROSS!
119

12 9
4 5
quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
4 5 6
1 2 3
partition(arr,1,3)
left
right
right & left CROSS!
2 – return new position of pivot
return 2
120

12 9
4 5
quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
4 5 6
1 2 3
121

12 9
4 5
quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
4 5 6
1 2 3
partition(arr,1,2)
122

12 9
4 5
quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
4 5 6
1 2 3
123

12 9
4 5
quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
6
3
4 5
1 2
124

12 9
4 5
quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
6
3
4 5
1 2
partition(arr,4,5)
125

9 12
4 5
quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
6
3
4 5
1 2
partition(arr,4,5)
126

quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
6
3
4 5
1 2
quickSort(arr,4,5)
9 12
4 5
quickSort(arr,6,5)
127

quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
6
3
4 5
1 2
quickSort(arr,4,5)
9 12
4 5
partition(arr,4,5)
quickSort(arr,6,5)
128

quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
6
3
4 5
1 2
quickSort(arr,4,5)
9 12
4 5
quickSort(arr,6,5)
129

quickSort(arr,0,5)
quickSort(arr,0,0)
3
0
quickSort(arr,1,3)
6
3
4 5
1 2
quickSort(arr,4,5)
9
12
4
5
quickSort(arr,4,4)
quickSort(arr,5,5)
quickSort(arr,6,5)
130

Quick Sort
131
Properties:
• Not -stable Sorting
• In-place sorting (O(log n) extra space)
• Not Adaptive
• O(n2) time, typically O(nlogn)

132
• Best Case:
Divides the array into two partitions of equal size, therefore
T(n) = 2T(n/2) + O(n) , Solving this recurrence we get,
T(n)=O(nlogn)
• Worst case:
when one partition contains the n-1 elements and another partition contains
only one element. Therefore its recurrence relation is:
T(n) = T(n-1) + O(n), Solving this recurrence we get, T(n)=O(n2)
• Average case:
Good and bad splits are randomly distributed across throughout the tree
T1(n)= 2T'(n/2) + O(n) Balanced
T'(n)= T(n –1) + O(n) Unbalanced
Solving:
B(n)= 2(B(n/2 –1) + Θ(n/2)) + Θ(n)
= 2B(n/2 –1) + Θ(n)
= O(nlogn)
=>T(n)=O(nlogn)
Analysis of Quick Sort

133
Merge Sort
Merge sort is divide and conquer algorithm. It is recursive algorithm
having three steps. To sort an array A[l . . r]:
• Divide
Divide the n-element sequence to be sorted into two sub-sequences of
n/2 elements
• Conquer
Sort the sub-sequences recursively using merge sort. When the size of
the sequences is 1 there is nothing more to do
•Combine
Merge the two sorted sub-sequences into single sorted array. Keep
track of smallest element in each sorted half and inset smallest of two
elements into auxiliary array. Repeat this until done.

134
MergeSort(A, l, r)
{
If(l<r)
{
m = (l+r)/2
MergeSort(A, l, m)
MergeSort(A, m+1, r)
Merge(A, l, m+1, r)
}
}
Algorithm:

Merge operation
Merge(A, B, l, m, r)
{
x= l, y=m, k =l;
While(x<m && y<=r)
{
if(A[x] < A[y])
{
B[k] = A[x];
k++; x++;
}
else
{
B[k] = A[y];
k++; y++;
}
} 135
while(x<m)
{
B[k] = A[x];
k++;x++;
}
while(y<=r)
{
B[k] = A[y];
k++; y++;
}
For(i =1;i<=r;i++)
{
A[i] = B[i];
}
} // end of merge

136
Example: a[]= {4, 7, 2, 6, 1, 4, 7, 3, 5, 2, 6}

Merge Sort
138
Properties:
 stable Sorting
 Not In-place sorting (O( n) extra space)
 Not Adaptive
 Time complexity: O(nlogn)

Merge Sort
139
Time Complexity:
Recurrence Relation for Merge sort:
T(n) = 1 if n=1
T(n) = 2 T(n/2) + O(n) if n>1
Solving this recurrence we get
T(n) = O(nlogn)
Space Complexity:
It uses one extra array and some extra variables during sorting,
therefore,
Space Complexity = 2n + c = O(n)

Unit 7 sorting

Recommended

More Related Content

What's hot (19)

Similar to Unit 7 sorting (20)

More from Dabbal Singh Mahara (17)

Recently uploaded (20)

Unit 7 sorting