Unit commitment in power system
- 1. Unit Commitment Daniel Kirschen © 2011 Daniel Kirschen and the University of Washington 1
- 2. Economic Dispatch: Problem Definition • Given load • Given set of units on-line • How much should each unit generate to meet this load at minimum cost? © 2011 Daniel Kirschen and the University of Washington 2 A B C L
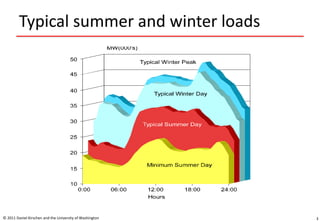
- 3. Typical summer and winter loads © 2011 Daniel Kirschen and the University of Washington 3
- 4. Unit Commitment • Given load profile (e.g. values of the load for each hour of a day) • Given set of units available • When should each unit be started, stopped and how much should it generate to meet the load at minimum cost? © 2011 Daniel Kirschen and the University of Washington 4 G G G Load Profile ? ? ?
- 5. A Simple Example • Unit 1: • PMin = 250 MW, PMax = 600 MW • C1 = 510.0 + 7.9 P1 + 0.00172 P1 2 $/h • Unit 2: • PMin = 200 MW, PMax = 400 MW • C2 = 310.0 + 7.85 P2 + 0.00194 P2 2 $/h • Unit 3: • PMin = 150 MW, PMax = 500 MW • C3 = 78.0 + 9.56 P3 + 0.00694 P3 2 $/h • What combination of units 1, 2 and 3 will produce 550 MW at minimum cost? • How much should each unit in that combination generate? © 2011 Daniel Kirschen and the University of Washington 5
- 6. Cost of the various combinations © 2011 Daniel Kirschen and the University of Washington 6
- 7. Observations on the example: • Far too few units committed: Can’t meet the demand • Not enough units committed: Some units operate above optimum • Too many units committed: Some units below optimum • Far too many units committed: Minimum generation exceeds demand • No-load cost affects choice of optimal combination © 2011 Daniel Kirschen and the University of Washington 7
- 8. A more ambitious example • Optimal generation schedule for a load profile • Decompose the profile into a set of period • Assume load is constant over each period • For each time period, which units should be committed to generate at minimum cost during that period? © 2011 Daniel Kirschen and the University of Washington 8 Load Time 1260 18 24 500 1000
- 9. Optimal combination for each hour © 2011 Daniel Kirschen and the University of Washington 9
- 10. Matching the combinations to the load © 2011 Daniel Kirschen and the University of Washington 10 Load Time 1260 18 24 Unit 1 Unit 2 Unit 3
- 11. Issues • Must consider constraints – Unit constraints – System constraints • Some constraints create a link between periods • Start-up costs – Cost incurred when we start a generating unit – Different units have different start-up costs • Curse of dimensionality © 2011 Daniel Kirschen and the University of Washington 11
- 12. Unit Constraints • Constraints that affect each unit individually: –Maximum generating capacity –Minimum stable generation –Minimum “up time” –Minimum “down time” –Ramp rate © 2011 Daniel Kirschen and the University of Washington 12
- 13. Notations © 2011 Daniel Kirschen and the University of Washington 13 u(i,t): Status of unit i at period t x(i,t): Power produced by unit i during period t Unit i is on during period tu(i,t) =1: Unit i is off during period tu(i,t) = 0 :
- 14. Minimum up- and down-time • Minimum up time – Once a unit is running it may not be shut down immediately: • Minimum down time – Once a unit is shut down, it may not be started immediately © 2011 Daniel Kirschen and the University of Washington 14 If u(i,t) =1 and ti up < ti up,min then u(i,t +1) =1 If u(i,t) = 0 and ti down < ti down,min then u(i,t +1) = 0
- 15. Ramp rates • Maximum ramp rates – To avoid damaging the turbine, the electrical output of a unit cannot change by more than a certain amount over a period of time: © 2011 Daniel Kirschen and the University of Washington 15 x i,t +1( )- x i,t( )£ DPi up,max x(i,t)- x(i,t +1) £ DPi down,max Maximum ramp up rate constraint: Maximum ramp down rate constraint:
- 16. System Constraints • Constraints that affect more than one unit – Load/generation balance – Reserve generation capacity – Emission constraints – Network constraints © 2011 Daniel Kirschen and the University of Washington 16
- 17. Load/Generation Balance Constraint © 2011 Daniel Kirschen and the University of Washington 17 u(i,t)x(i,t) i=1 N å = L(t) N : Set of available units
- 18. Reserve Capacity Constraint • Unanticipated loss of a generating unit or an interconnection causes unacceptable frequency drop if not corrected rapidly • Need to increase production from other units to keep frequency drop within acceptable limits • Rapid increase in production only possible if committed units are not all operating at their maximum capacity © 2011 Daniel Kirschen and the University of Washington 18 u(i,t) i=1 N å Pi max ³ L(t)+ R(t) R(t): Reserve requirement at time t
- 19. How much reserve? • Protect the system against “credible outages” • Deterministic criteria: – Capacity of largest unit or interconnection – Percentage of peak load • Probabilistic criteria: – Takes into account the number and size of the committed units as well as their outage rate © 2011 Daniel Kirschen and the University of Washington 19
- 20. Types of Reserve • Spinning reserve – Primary • Quick response for a short time – Secondary • Slower response for a longer time • Tertiary reserve – Replace primary and secondary reserve to protect against another outage – Provided by units that can start quickly (e.g. open cycle gas turbines) – Also called scheduled or off-line reserve © 2011 Daniel Kirschen and the University of Washington 20
- 21. Types of Reserve • Positive reserve – Increase output when generation < load • Negative reserve – Decrease output when generation > load • Other sources of reserve: – Pumped hydro plants – Demand reduction (e.g. voluntary load shedding) • Reserve must be spread around the network – Must be able to deploy reserve even if the network is congested © 2011 Daniel Kirschen and the University of Washington 21
- 22. Cost of Reserve • Reserve has a cost even when it is not called • More units scheduled than required – Units not operated at their maximum efficiency – Extra start up costs • Must build units capable of rapid response • Cost of reserve proportionally larger in small systems • Important driver for the creation of interconnections between systems © 2011 Daniel Kirschen and the University of Washington 22
- 23. Environmental constraints • Scheduling of generating units may be affected by environmental constraints • Constraints on pollutants such SO2, NOx – Various forms: • Limit on each plant at each hour • Limit on plant over a year • Limit on a group of plants over a year • Constraints on hydro generation – Protection of wildlife – Navigation, recreation © 2011 Daniel Kirschen and the University of Washington 23
- 24. Network Constraints • Transmission network may have an effect on the commitment of units – Some units must run to provide voltage support – The output of some units may be limited because their output would exceed the transmission capacity of the network © 2011 Daniel Kirschen and the University of Washington 24 Cheap generators May be “constrained off” More expensive generator May be “constrained on” A B
- 25. Start-up Costs • Thermal units must be “warmed up” before they can be brought on-line • Warming up a unit costs money • Start-up cost depends on time unit has been off © 2011 Daniel Kirschen and the University of Washington 25 SCi (ti OFF ) = ai + bi (1 - e - ti OFF t i ) ti OFF αi αi + βi
- 26. Start-up Costs • Need to “balance” start-up costs and running costs • Example: – Diesel generator: low start-up cost, high running cost – Coal plant: high start-up cost, low running cost • Issues: – How long should a unit run to “recover” its start-up cost? – Start-up one more large unit or a diesel generator to cover the peak? – Shutdown one more unit at night or run several units part- loaded? © 2011 Daniel Kirschen and the University of Washington 26
- 27. Summary • Some constraints link periods together • Minimizing the total cost (start-up + running) must be done over the whole period of study • Generation scheduling or unit commitment is a more general problem than economic dispatch • Economic dispatch is a sub-problem of generation scheduling © 2011 Daniel Kirschen and the University of Washington 27
- 28. Flexible Plants • Power output can be adjusted (within limits) • Examples: – Coal-fired – Oil-fired – Open cycle gas turbines – Combined cycle gas turbines – Hydro plants with storage • Status and power output can be optimized © 2011 Daniel Kirschen and the University of Washington 28 Thermal units
- 29. Inflexible Plants • Power output cannot be adjusted for technical or commercial reasons • Examples: – Nuclear – Run-of-the-river hydro – Renewables (wind, solar,…) – Combined heat and power (CHP, cogeneration) • Output treated as given when optimizing © 2011 Daniel Kirschen and the University of Washington 29
- 30. Solving the Unit Commitment Problem • Decision variables: – Status of each unit at each period: – Output of each unit at each period: • Combination of integer and continuous variables © 2011 Daniel Kirschen and the University of Washington 30 u(i,t) Î 0,1{ } " i,t x(i,t) Î 0, Pi min ;Pi max éë ùû{ } " i,t
- 31. Optimization with integer variables • Continuous variables – Can follow the gradients or use LP – Any value within the feasible set is OK • Discrete variables – There is no gradient – Can only take a finite number of values – Problem is not convex – Must try combinations of discrete values © 2011 Daniel Kirschen and the University of Washington 31
- 32. How many combinations are there? © 2011 Daniel Kirschen and the University of Washington 32 • Examples – 3 units: 8 possible states – N units: 2N possible states 111 110 101 100 011 010 001 000
- 33. How many solutions are there anyway? © 2011 Daniel Kirschen and the University of Washington 33 1 2 3 4 5 6T= • Optimization over a time horizon divided into intervals • A solution is a path linking one combination at each interval • How many such paths are there?
- 34. How many solutions are there anyway? © 2011 Daniel Kirschen and the University of Washington 34 1 2 3 4 5 6T= Optimization over a time horizon divided into intervals A solution is a path linking one combination at each interval How many such path are there? Answer: 2N ( ) 2N ( )… 2N ( ) = 2N ( )T
- 35. The Curse of Dimensionality • Example: 5 units, 24 hours • Processing 109 combinations/second, this would take 1.9 1019 years to solve • There are 100’s of units in large power systems... • Many of these combinations do not satisfy the constraints © 2011 Daniel Kirschen and the University of Washington 35 2N ( ) T = 25 ( ) 24 = 6.21035 combinations
- 36. How do you Beat the Curse? Brute force approach won’t work! • Need to be smart • Try only a small subset of all combinations • Can’t guarantee optimality of the solution • Try to get as close as possible within a reasonable amount of time © 2011 Daniel Kirschen and the University of Washington 36
- 37. Main Solution Techniques • Characteristics of a good technique – Solution close to the optimum – Reasonable computing time – Ability to model constraints • Priority list / heuristic approach • Dynamic programming • Lagrangian relaxation • Mixed Integer Programming © 2011 Daniel Kirschen and the University of Washington 37 State of the art
- 38. A Simple Unit Commitment Example © 2011 Daniel Kirschen and the University of Washington 38
- 39. Unit Data © 2011 Daniel Kirschen and the University of Washington 39 Unit Pmin (MW) Pmax (MW) Min up (h) Min down (h) No-load cost ($) Marginal cost ($/MWh) Start-up cost ($) Initial status A 150 250 3 3 0 10 1,000 ON B 50 100 2 1 0 12 600 OFF C 10 50 1 1 0 20 100 OFF
- 40. Demand Data © 2011 Daniel Kirschen and the University of Washington 40 Hourly Demand 0 50 100 150 200 250 300 350 1 2 3 Hours Load Reserve requirements are not considered
- 41. Feasible Unit Combinations (states) © 2011 Daniel Kirschen and the University of Washington 41 Combinations Pmin Pmax A B C 1 1 1 210 400 1 1 0 200 350 1 0 1 160 300 1 0 0 150 250 0 1 1 60 150 0 1 0 50 100 0 0 1 10 50 0 0 0 0 0 1 2 3 150 300 200
- 42. Transitions between feasible combinations © 2011 Daniel Kirschen and the University of Washington 42 A B C 1 1 1 1 1 0 1 0 1 1 0 0 0 1 1 1 2 3 Initial State
- 43. Infeasible transitions: Minimum down time of unit A © 2011 Daniel Kirschen and the University of Washington 43 A B C 1 1 1 1 1 0 1 0 1 1 0 0 0 1 1 1 2 3 Initial State TD TU A 3 3 B 1 2 C 1 1
- 44. Infeasible transitions: Minimum up time of unit B © 2011 Daniel Kirschen and the University of Washington 44 A B C 1 1 1 1 1 0 1 0 1 1 0 0 0 1 1 1 2 3 Initial State TD TU A 3 3 B 1 2 C 1 1
- 45. Feasible transitions © 2011 Daniel Kirschen and the University of Washington 45 A B C 1 1 1 1 1 0 1 0 1 1 0 0 0 1 1 1 2 3 Initial State
- 46. Operating costs © 2011 Daniel Kirschen and the University of Washington 46 1 1 1 1 1 0 1 0 1 1 0 0 1 4 3 2 5 6 7
- 47. Economic dispatch © 2011 Daniel Kirschen and the University of Washington 47 State Load PA PB PC Cost 1 150 150 0 0 1500 2 300 250 0 50 3500 3 300 250 50 0 3100 4 300 240 50 10 3200 5 200 200 0 0 2000 6 200 190 0 10 2100 7 200 150 50 0 2100 Unit Pmin Pmax No-load cost Marginal cost A 150 250 0 10 B 50 100 0 12 C 10 50 0 20
- 48. Operating costs © 2011 Daniel Kirschen and the University of Washington 48 1 1 1 1 1 0 1 0 1 1 0 0 1 4 3 2 5 6 7 $1500 $3500 $3100 $3200 $2000 $2100 $2100
- 49. Start-up costs © 2011 Daniel Kirschen and the University of Washington 49 1 1 1 1 1 0 1 0 1 1 0 0 1 4 3 2 5 6 7 $1500 $3500 $3100 $3200 $2000 $2100 $2100 Unit Start-up cost A 1000 B 600 C 100 $0 $0 $0 $0 $0 $600 $100 $600 $700
- 50. Accumulated costs © 2011 Daniel Kirschen and the University of Washington 50 1 1 1 1 1 0 1 0 1 1 0 0 1 4 3 2 5 6 7 $1500 $3500 $3100 $3200 $2000 $2100 $2100 $1500 $5100 $5200 $5400 $7300 $7200 $7100 $0 $0 $0 $0 $0 $600 $100 $600 $700
- 51. Total costs © 2011 Daniel Kirschen and the University of Washington 51 1 1 1 1 1 0 1 0 1 1 0 0 1 4 3 2 5 6 7 $7300 $7200 $7100 Lowest total cost
- 52. Optimal solution © 2011 Daniel Kirschen and the University of Washington 52 1 1 1 1 1 0 1 0 1 1 0 0 1 2 5 $7100
- 53. Notes • This example is intended to illustrate the principles of unit commitment • Some constraints have been ignored and others artificially tightened to simplify the problem and make it solvable by hand • Therefore it does not illustrate the true complexity of the problem • The solution method used in this example is based on dynamic programming. This technique is no longer used in industry because it only works for small systems (< 20 units) © 2011 Daniel Kirschen and the University of Washington 53