Unit26 shortest pathalgorithm

Shortest Path Algorithm What is the Shortest Path Problem? Is the shortest path problem well defined? The Dijkstra's Algorithm for Shortest Path Problem. Implementation Dijkstra's Algorithm

What is the shortest path problem? In an edge-weighted graph, the weight of an edge measures the cost of traveling that edge. For example, in a graph representing a network of airports, the weights could represent: distance, cost or time. Such a graph could be used to answer any of the following: What is the fastest way to get from A to B? Which route from A to B is the least expensive? What is the shortest possible distance from A to B? Each of these questions is an instance of the same problem: The shortest path problem!

Is the shortest path problem well defined? If all the edges in a graph have non-negative weights, then it is possible to find the shortest path from any two vertices. For example, in the figure below, the shortest path from B to F is { B, A, C, E, F } with a total cost of nine. Thus, the problem is well defined for a graph that contains non-negative weights.

Is the shortest path problem well defined? - Cont'd Things get difficult for a graph with negative weights. For example, the path D, A, C, E, F costs 4 even though the edge (D, A) costs 5 -- the longer the less costly. The problem gets even worse if the graph has a negative cost cycle. e.g. {D, A, C, D} A solution can be found even for negative-weight graphs but not for graphs involving negative cost cycles. {D, A, C, D, A, C, E, F} = 2 {D, A, C, D, A, C, D, A, C, E, F} = 0

The Dijkstra's Algorithm Dijkstra's algorithm solves the single-source shortest path problem for a non-negative weights graph. It finds the shortest path from an initial vertex, say s, to all the other vertices.

The Dijkstra's Algorithm Cont'd // Let V be the set of all vertices in G, and s the start vertex. for(each vertex v){ currentDistance(s-v) = ∞; predecessor(v) = undefined; } currentDistance(s-s) = 0; T = V; while(T   ){ v = a vertex in T with minimal currentDistance from s; T= T – {v}; for(each vertex u adjacent to v and in T){ if(currentDistance(s-u) > currentDistance(s-v) + weight(edge(vu)){ currentDistance(s-u) = currentDistance(s-v) + weight(edge(vu)); predecessor(u) = v; } } } For each vertex, the algorithm keeps track of its current distance from the starting vertex and the predecessor on the current path

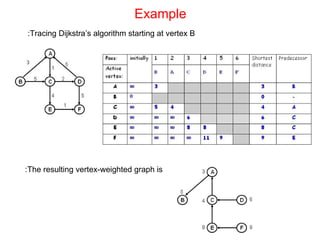
Example Tracing Dijkstra’s algorithm starting at vertex B: The resulting vertex-weighted graph is:

Data structures required The implementation of Dijkstra's algorithm uses the Entry structure, which contains the following three fields: know : a boolean variable indicating whether the shortest path to v is known, initially false for all vertices. distance : the shortest known distance from s to v, initially infinity for all vertices except that of s which is 0. predecessor : the predecessor of v on the path from s to v, initially unknown for all vertices. public class Algorithms{ static final class Entry{ boolean known; int distance; Vertex predecessor; Entry(){ known = false; distance = Integer.MAX_VALUE; predecessor = null; } }

Implementation of Dijkstra's Algorithm The dijkstrasAlgorithm method shown below takes two arguments, a directed graph and the starting vertex. The method returns a vertex-weighted Digraph from which the shortest path from s to any vertex can be found. Since in each pass, the vertex with the smallest known distance is chosen, a minimum priority queue is used to store the vertices. public static Graph dijkstrasAlgorithm(Graph g, Vertex start){ int n = g.getNumberOfVertices(); Entry table[] = new Entry[n]; for(int v = 0; v < n; v++) table[v] = new Entry(); table[g.getIndex(start)].distance = 0; PriorityQueue queue = new BinaryHeap( g.getNumberOfEdges()); queue.enqueue(new Association(new Integer(0), start));

Implementation of Dijkstra's Algorithm - Cont'd while(!queue.isEmpty()) { Association association = (Association)queue.dequeueMin(); Vertex v1 = (Vertex) association.getValue(); int n1 = g.getIndex(v1); if(!table[n1].known){ table[n1].known = true; Iterator p = v1.getEmanatingEdges(); while (p.hasNext()){ Edge edge = (Edge) p.next(); Vertex v2 = edge.getMate(v1); int n2 = g.getIndex(v2); Integer weight = (Integer) edge.getWeight(); int d = table[n1].distance + weight.intValue(); if(table[n2].distance > d){ table[n2].distance = d; table[n2].predecessor = v1; queue.enqueue(new Association(d, v2)); } } } }

Implementation of Dijkstra's Algorithm Cont'd Graph result = new GraphAsLists(true);//Result is Digraph Iterator it = g.getVertices(); while (it.hasNext()){ Vertex v = (Vertex) it.next(); result.addVertex(v.getLabel(), new Integer(table[g.getIndex(v)].distance)); } it = g.getVertices(); while (it.hasNext()){ Vertex v = (Vertex) it.next(); if (v != start){ String from = v.getLabel(); String to = table[g.getIndex(v)].predecessor.getLabel(); result.addEdge(from, to); } } return result; }

Review Questions Use the graph Gc shown above to trace the execution of Dijkstra's algorithm as it solves the shortest path problem starting from vertex a. Dijkstra's algorithm works as long as there are no negative edge weights. Given a graph that contains negative edge weights, we might be tempted to eliminate the negative weights by adding a constant weight to all of the edges. Explain why this does not work. Dijkstra's algorithm can be modified to deal with negative edge weights (but not negative cost cycles) by eliminating the known flag and by inserting a vertex back into the queue every time its tentative distance decreases. Implement this modified algorithm.

Unit26 shortest pathalgorithm

Recommended

More Related Content

What's hot (20)

Viewers also liked (20)

Similar to Unit26 shortest pathalgorithm (20)

Recently uploaded (20)

Unit26 shortest pathalgorithm