Unit-III_3R-CRYPTO_2021-22_VSM.pptx

Unit:III
CRYPTOGRAPHY
Department of Computer Science and Engineering
Shri Sant Gajanan Maharaj College of Engineering, Shegaon
Prof. V. S. Mahalle

Public-Key Cryptography:
1) Public Key Cryptography Principles,
2) Public Key Cryptography Algorithms,
3) Digital Signatures,
4) Key Management.

o Asymmetric Key Algorithms, Digital Signatures and RSA:
 Introduction to Asymmetric Key Cryptography
 Symmetric Vs Asymmetric Cryptography
 The RSAAlgorithm
 Digital Signatures
 Knapsack and other Algorithms.

INTRODUCTION
• Classification of Cryptosystem w. r. t. Key:
[1] Symmetric Key Cryptosystem
[2] Asymmetric Key Cryptosystem

o Sender and recipient share a common key for encryption & decryption respectively.
• Basic terminologies:
Plain Text, Cipher Text, Secret Key, Encryption & Decryption.
• Algorithms:
DES, 2-DES/3-DES, AES, Blowfish, IDEA, RC5 & RC4.
• SYMMETRIC KEY CRYPTOGRAPHY / ENCRYPTION:
Also referred as Conventional / Private-key / Single-key / Secret key Cryptography.

• ASYMMETRIC KEY CRYPTOGRAPHY / ENCRYPTION:
Also referred as public key Cryptography.
• Major difference between symmetric & asymmetric key cryptography:
key is the difference means key(s) used.
• Symmetric means --> Only one Key i.e.
Use same key for encryption & decryption
• What is Problem? -->
Problem is how sender sends key to the receiver?.
• Asymmetric means --> Use two keys:
(1) Public Key
(2) Private Key
that means: every user on Network have two keys.

PuA =Public key of User A PuB = Public key of User B
PrA = Private Key of User A PrB = Private Key of User B
User-A
(Sender)
User-B
(Receiver)

Unit-III_3R-CRYPTO_2021-22_VSM.pptx

INTRODUCTION
Symmetric/Secret key
Cryptographic System & Algorithms:
(Symmetric Encryption & Decryption System & Algorithms)
KE = KD
Number of Keys Used: 1
(for Encryption & Decryption)
Key, K = Must kept secret.
(Only known to Sender & Receiver)
Encryption & Decryption Speed: Faster
Most commonly used Symmetric key
Cryptographic Algorithms: DES, AES
Asymmetric/Public key
Cryptographic System & Algorithms:
(Asymmetric Encryption & Decryption System & Algorithms)
KE ≠ KD
Number of Keys Used: 2
(2 keys for Encryption & 2 keys for Decryption)
One Key kept Secret = Private key
Other Key make public= Public key
Encryption & Decryption Speed: Slower
Most commonly used Symmetric key
Cryptographic Algorithms:RSA, Diffie-
Hellman

PUBLIC KEY CRYPTOGRAPHIC PRINCIPLES
• Public key cryptographic schemes are neither more nor less secure than private key
cryptographic scheme.
(Security depends on the key size for both).
• Public-key cryptography complements rather than replaces symmetric cryptography.
(Both also have issues with key distribution.)
• Public-key/two-key/asymmetric cryptography involves the use of two keys:
 Public-key, which may be known by anybody.
 Private-key, known only to the recipient.
Public-Key algorithms rely on one key for encryption and a different but related key for decryption.
• Asymmetric Cryptographic algorithms have the following important characteristics:
 It is computationally infeasible to find decryption key knowing only algorithm & encryption key.
 It is computationally easy to en/decrypt messages when the relevant (en/decrypt) key is known.
 Either of the two related keys can be used for encryption, with the other used for decryption

Steps involved in a public-key
encryption scheme are:
1.) Each user generates a pair of keys to be used
for encryption and decryption.
2.) Each user places one of the two keys in a
public register and the other key is kept private.
3.) If B wants to send a confidential message to
A, B encrypts the message using A’s public key.
4.) When A receives the message, she decrypts
it using her private key. Nobody else can decrypt
the message because that can only be done
using A’s private key.
5.) If a user wishes to change his keys –generate
another pair of keys and publish the public one:
no interaction with other users is needed.
Fig: Public Key Encryption Process
It has six ingredients: plaintext, encryption algorithm, public key, private key,
cipher-text & decryption algorithm.
Notations used in Public-key cryptography:
public key of B ==> PUB & Private Key of B ==> PRB
Public key of A==> PUA & Private key of A ==> PRA
B A
B wishes to send secret message M to A, then B perform
encryption operation on M using PUBto get cipher text C,
C = (PUB, M)
Receiver A will decrypt the message using his Private key & get M:
M = D(PR , C)
M
C
M

• The first attack on Public-key Cryptography is the attack on Authenticity.
• An attacker may impersonate user B: he sends a message E(PUA, M) and claims in the
message to be B.
To overcome this, B will encrypt
the message using his private key:
C = E(PRB, M).
Receiver decrypts using B’s public
key PUB.
M = D(PUB , C)
This shows the authenticity of the
sender because he is the only one
who knows the private key.
But, a drawback still exists. Anybody can decrypt the message using B’s public key. So, secrecy or
confidentiality is being compromised.
(Applications for public key cryptography: Digital Signature, Key exchange, Kerberos…)

• The main requirements of Public-key cryptography are:
i.e. The conditions that such algorithms must fulfill are:
1. Computationallyeasyfor apartyBto generate apair(publickey PUb,privatekey PRb).
2. Computationally Easy for sender A, knowing the public key & message M to be encrypted to generate
corresponding cipher text C:
3. Easy for the receiver B to decrypt cipher text C using private key to get original message.
4. Computationally infeasible foropponent, to determine private key knowing public key.
5. Computationally infeasible for opponent, to recover message M, knowing public key and ciphertext C
6. Either of the two keys can be used for encryption, with the other used for decryption:

RSA
Public Key Cryptography Algorithm
• Designer:
• Ron Rivest
• Adi Shamir
• Leonard Adleman
• Publication Year:
• 1977
• Based on Number theory :
• Prime Numbers
• Key Size used:
• 1024 to 4096 bits
• Algorithm involves 3-steps:
1) Key Generation: public & private keys
2) Encryption of Plain text
3) Decryption of Cipher text.
• Public key is known to every one.
• Message encrypted with public key can only be decrypted using private key.

Different steps of RSA for key generation, encryption & decryption
1. Choose two distinct large prime numbers.
Consider numbers: p & q
2. Compute Product:
n = p * q
3. Compute ᶲ(n),
ᶲ(n) = (p-1)(q-1)
Where ᶲ(n) = Euler’s Totient function
4. Choose integer, e
such that
1< e < ᶲ(n)
where e & ᶲ(n) are- Relatively prime(co-prime)
i.e. GCD(e, ᶲ(n)) = 1

5. Now, we get public key,
public key = (n,e)
6. Calculate d for private key,
d = e-1 (mod ᶲ(n))
7. We get private key,
private key = (n, d)
8) To get Cipher Text, encrypt bit pattern M
C = me (mod n)
9) To decrypt cipher text C & get Plain text M,
M = Cd (mod n)
• d * e = 1 mod ᶲ(n)
• d * e mod ᶲ(n) = 1

Example-1:
Given p =17 & q =11 two prime numbers & plain test M = 88
Compute
public key, private key, cipher text & original plain text form cipher text?
(i) Calculate product,
n = p*q = 17 * 11 = 187
(ii) Calculate ᶲ(n),
ᶲ(n) = (p-1) (q-1) = (17 -1) (11-1) = 160
(iii) Select e such that e is relatively prime to ᶲ(n) less than ᶲ(n) & greater than 1.
ᶲ(n) =160
Suppose we choose e =7,
Verify GCD(7, 160) = 1
7|7 2|160
|1 2|80
2|40
2|20 7 = 7,
2|10 160 = 2,2,2,2,2,5,
5|5
|1 GCD = 1*1 = 1
1
1

(iv) Determine d,
such that d*e mod160 = 1 & d <160
Therefore, select d = 23 Because(d*e), (23 *7) = 161
161 mod 160 = 1
(v) Public key & Private key:
public Key = {7,187}
private Key = {23,187}
887Mod 187 = 11 1123Mod 187 = 88
88
11
88
For encryption,
C = 887Mod 187 = 11
( me mod n)
For decryption,
M = 1123 mod187 = 88

Example-2 & 3:
Given p =61 & q =53 two prime numbers 0r take p =47 & q = 71
Compute
public key, private key, cipher text & original plain text form cipher text?
Example-4:
Given p =3 & q =11 two prime numbers
find e & d?

Diffie-Hellman Key Exchange
E D
P C P
Encryption
Key
Decryption Key
KE KD
• Cryptographic System with Key:
o For encrypting plain text to get cipher text &
o For decrypting cipher text to get original plain text.
1) Symmetric Encryption:
2) Asymmetric Encryption:
KE = KD
KE ≠ KD
• Algorithms: DES & AES
• Algorithms: RSA
Now, we want
• Secret key, used in encryption process is
securely send to Receiver.
• How secret key used in symmetric
encryption is shared between two
users?
• How to verify key exchange between
two user is successful?.
• One way is to generate secret key,
• at sender site & at receiver site.
•Every user have two keys, public & private keys.
•If one key is used for encryption, then other key is use for decryption.

• In Deffie-Hellman,
o For encryption of plain text & decryption of cipher text:
 Symmetric Encryption Technique is Used (Same key is used).
o For Exchanging key between Sender & Receiver:
 Diffie-Hellman key exchange algorithm is used.
 This uses Asymmetric Encryption Technique.
 i.e. Public key
&
Private key
Uses ==>
• To generate Secret Key
at
Sender site & Receiver site
And
The key generated at sender & receiver sites are matched, then we
can say,
Secret Key Exchange between Sender & Receiver is successful.

ALGORITHM
(i) Assume Prime Number, q
(ii) Select α,
such that
α must be primitive root of q
&
α < q
(iii) Calculate public key of user A & public key user B using their Private key.
Assume:
X as Private key == >
Y as Public key
XA ----> Private key of A
XB ----> Private key of B
&
YA ----> Public key of A
YB ----> Public key of B

(a) Calculate Public Key of User A===> YA ?,
Using his Private Key XA and XA < q
(b) Calculate Public Key of User B == > YB ?
Using his Private Key XB and XB < q
(iv) Generate Secret Key K at Sender site & at Receiver site:
• Public keys are available to all.
YA = α
XA mod q
YB = α
XB mod q
K ->
Key Generated
at Sender site
K = (YB) XA mod q
K ->
Key Generated
at Receiver site
K = (YA) XB mod q
=
• Keys Generated must
be equal at both the
sites, then
we can say, Key
Exchange is successful.

• EXAMPLE:
Prime Number q = 11
Private Key of A, XA = 8
Private Key of B, XB = 4
Determine Public key of A & Public Key of B?
Also Generate secret key at both sender & receiver sites & verify Key is exchange successfully or not?
• Select α ?
α should be Primitive root of 11
• What do you mean by primitive root? How can we find primitive root?
We say α is a Primitive root of q,
if
α mod q, α
2 mod q, α
3 mod q ………… α
q-1 mod q
should give result ===>
{1, 2, 3, 4, … q-1} <--- Value should not be repeated.
This condition satisfied, then we say that,
α is a Primitive root of q.

Select α ?
Power of α 1 2 3 4 5 6 7 8 9 10
1 1 1 1 1 1 1 1 1 1 1
2 2 4 8 5 10 9 7 3 6 1
3 3 9 5 4
4
5
6
7
8
Number
Selecting, α
q-1
Suppose we consider α = 1,
then verify 1 is primitive root of 11 or not. Put α = 1 in equation,
α mod q, α
2 mod q, α
3 mod q ………… α
q-1 mod q
If result is {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} then 1 is primitive root of 11.
If not then consider α = 2 :
2
5
7

Now we selected α = 2 & Given XA = 8.
Determine YA?
Now, α = 2 & Given XB = 4.
Determine YB?
YA = α
XA mod q
=2
8
mod 11
= 256 mod 11
YA=3
YB = α
XB mod q
= 2
4
mod 11
=16 mod 11
= 5 (public key)

• Calculate Secret Key, K at Sender & Receiver sites:
XA = 8
XB = 4
YA = 3
YB= 5
K ->
Key Generated
at Sender site
K = (YB) XA mod q
K = 4
K ->
Key Generated
at Receiver site
K = (YA) XB mod q
K = 4

Digital Signature
• Digital Signature ensures,
Message Authentication
Message Integrity
Non-repudiation of Message.
• Signature:
That is the part of document.
One-to- many relationship between a signature & documents. (one signature & many
documents)
• Digital Signature:
It is considered as separate document.
One-to-one relationship between signature & message. (each & every message signed
differently, no two message have the same signature)

Digital Signature Model
• Uses Public Key Cryptographic Technique.
M M M
E
PUB
PRB
D
User A User B
Case-I
M M M
E
PRA
PUA
D
User A User B
Case-II
Observe Case-II:
No one have A’s private key & no one can create a cipher text that decrypt with A’s public key.
==>Authentication is achieved.
It is impossible to attacker to alter the message, because it is encrypted using A’a private key.
==>Integrity is achieved.
If message is encrypted using sender’s private key, then we call it as ==>a Digital Signature.

Digital Signature Models
A B
Transmit message
M
Digital
Signature
Generation
Algorithm
s
A’s
Private key
M
S
Digital
Signature
Verification
Algorithm
A’s Public Key
Return Signature
Able to verify that whether is valid
or not.
If Signature is valid, then B is sure
that the message send by A.
Fig. Digital Signature model without hash function
A’s Signature
For M

A B
M
E
H
S
A’s
Private key
h
A’s Signature
For M
S
D
h’
Compare
Returns Signature is Valid or Invalid
Fig. Digital Signature model with hash function

Message Signing Procedure
M
Signing
Algorithm
A’s
Private key
Verifying
Algorithm
M
A’s
Public key
User
A
User
B
• Signing algorithm, signs the message.
• The message & signature sent to the receiver.
• The receiver receives the message & signature and applies to verifying algorithm.
• If it matches, then message is accepted, otherwise it is rejected.

Digest Signing Procedure
M
Hash Sign
A’s
Private Key
Verify Hash
A’s
Public Key M
S
• Authentication:
Message is received from actual sender.
• Integrity:
Hash code is generated, If hash matched that means message not modified.
• Non Repudiation:
Suppose A send signed message to B and B want to ensure it is from A, A never
denied that.

Digital Signature Schemes
1) Digital Signature using RSA approach:
M
H E
PRA,
h
A
M
h
H h
D
PUA
Compare
SHA-1/SHA-512
2) Digital Signature Standard(DSS)/Digital Signature Algorithm approach(DSA):
M H Signature
Algorithm
// M
S
r
Signature
verification
Algorithm
H
Compare
G PRA
K
Random
No.
h
s,r ---> Signature Components

Key Management
• How can you distribute the public key?
• Every uses have public key & private key.
A
A want to sent message to C. How A will get the public key of C?
How to distribute the public key, that is called key management.
Different techniques for distribution of public key:
1. Public announcement
2. Publically available dictionary (any body can change)
3. Public key authority (trusted third part, maintain dictionary)
4. Public key certificate (I want to send message to c , give me public key of C, issue a
certificate, that contains public key)
C
B
D

Public key certificate
• Public key certificate can be used by participants to exchange key.
• Each certificate, containing a public key and other information, is created by a certificate
authority and is given to the participant with matching private key.
• A participant conveys its key information to another by transmitting its certificate.
• Other participants can verify that the certificate was created by the authority.
C (Ed(auth)(tt, idc, Pub)
A
(will verify auth
sign)
Decript it using
auth Puauth)

Every user have their certificate issued & signed certificate authority.
Public-key distribution of secret key:

Message Authentication
• What is message authentication
• Why we need message authentication
• Different types of message authentication

User A User B
Hacker
Insecure channel
Message
“help Sita”
User A User B
Hacker
Insecure channel
Message
“kill Sita”
User A User B
Hacker
Insecure channel
Message
“kill Sita”
Understanding the Problem:
While sharing messages (files/
emails), there may be chance of
alteration of message in transit.
We need a mechanism, to
authenticate a message. i.e. How can
we check the authenticity of a
message?
It assures that
(i)message received are exactly as send
(i.e. contain no modification, insertion, deletion)
(ii) Identity of sender is valid.
i.e. A & B are Perfect user:
B receives message from A only.
A send message to B only
Message Authentication:
Third party can listen communication between A & B
Hacker caught the message & changes the content.
B consider, it is from A & according to message, he perform action.

Types of Authentications
(Different ways to achieve an authentication)
1. Message Encryption:
cipher text ---> act as Authenticator
i.e.
Receiver Authenticated by Sender
Sender Authenticated by Receiver
2. Message Authentication Code(MAC):
We have authentication function C with message M & secret key k.
C( M, k) = Fixed Length Code
3. Hash functions:
We have Hash function H with message M & it is independent of key k.
The output we get is fixed length code.
H(M) = Fixed Length Code
This process done only through cipher text.
Called MAC or Message Digest
Act as Authenticator
Authentication function
Called Hash Code, h
Act as Authenticator

1. Message Encryption:
M M M
E
k
D
k
User A User B
• Key k, shared between Sender and Receiver only.
• Cipher text act an Authenticator. Only receiver is able to decrypt the cipher text to get original message.
• Confidentiality is achieved (provided)
• Authentication is also achieved, but it is better to understand Authentication in
Asymmetric Cryptography.
• Major Problem of Symmetric Encryption: Key distribution
(How to send secret key to receiver site for decryption)
a) Symmetric Encryption:

b) Asymmetric Encryption (public key encryption):
• How it provide Confidentiality , Authentication?
• Case-I:
M M M
E
PUB
PRB
D
User A User B
PUA, PRA, PUB, PRB,
• Confidentiality:
“Unauthorized user should not get message. i.e. Only authorized user have access to message”
When we are using public key of user B for encryption, then private key of user B must be needed for decryption.
Public key available to all -----> Any user can encrypt the message & send to receiver.
i.e. No authentication is possible.
But for decryption, we require private key & it is available only with user B. The message is decrypted only
with user B’s private key. Only user B can decrypt the received message.
Therefore, Confidentiality is achieved but Authentication fails.

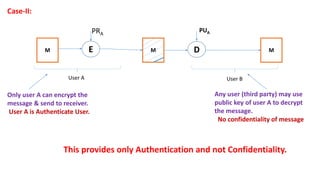
M M M
E
PRA
PUA
D
User A User B
Case-II:
Only user A can encrypt the
message & send to receiver.
User A is Authenticate User.
Any user (third party) may use
public key of user A to decrypt
the message.
No confidentiality of message
This provides only Authentication and not Confidentiality.

Case-III:
M M M
E
PRA
PRB
D
User A User B
E
PUB
M M
M D
PUA
Message encrypted using Private key of A: message Only decrypt using A’s public key.
Message encrypted using public key of B: message Only decrypt using B’s private key.
Both Authentication and Confidentiality is Achieved.

2. Message Authentication Code(MAC):
• MAC function act as an Authenticator.
C(M , k) ---> It takes variable length message M and secret key k as input and
Produces an Authentication Code.
User A User B
Secret key Secret key
M
k
MAC(generated)
M
C
k A
M
MAC
M
MAC
MAC(appende)
C
Compared
Append
Fixed Length Code
There is no encryption,
Therefore,
No confidentiality
MAC is used to
authenticate a message.
Authenticity is there
Help sita + MAC
AEF123
M
K=abc K=abc
AEF123
If message altered, then different MAC

M
C
k1 A
M
MAC
M
MAC MAC(appende)
Compared
Append
Fixed Length Code
E
k2
D
k2
C
M
MA
C
MAC
If equal, then
data is send
by perfect
Sender.
Authenticity
is there.

3. Hash function:
Hash code act as an authenticator,
independent from key
H(M) = fixed length code
Anybody can decrypt the hash code--> Drawback of this
M
H E
PRA,
h
A
M
h
H h
D
PUA
Compare
M
H E
PRA,
A E
k
M
h
D
k
M
h
D
H

User name: VSM
Password: VSM12
Sign up
User name: VSM
Password: fdfdfdfdf
MD-5
User name: VSM
Password: abddddeeertretretr
Sign in
User name: VSM
Password: fdfdfdfdff
1. The hash size is always fixed.
2. Hash function is non reversible. (hash function also
called as one way hash function..
3. Hash result can not collide.
4. If I change even one bit of the I/P from right or left
then entire has should change.

SHA: SECURE HASH ALGORITHM
• Developed by NIST in 1995.
• SHA algorithms are based on MD-5 Algorithm.
• Based on different digest lengths, SHA include algorithms such as
SHA-1, SHA-256, SHA-384, SHA-512
• SHA called secure because it is computationally infeasible to find a message which
corresponds to a given message digest. Also not produces the same digest for two
different message.
• The most commonly used hash function from SHA family is SHA-1 is used in SSL/TLS, PGP,
SSH, MIME & IPSec for security & authentication purposes./

SHA-1: SECURE HASH ALGORITHM-1
• SHA-1 is the extension of MD-5 algorithm. i.e. Similar to MD-5 with small modification.
• SHA-1 having 5-steps, similar to the steps in MD-5.
• In SHA-1,
• Input is plain text message:-
- Message of Arbitrary length (Variable length message)
- Message length should be < 264 bits.
(i.e. SHA-1 work with any I/P message that is less than 264 bits in length.)
• Output: Message digest.
- 160 bits fixed length Message digest
By knowing above, we can proceed the SHA-1 algorithm.
Different steps & processes of SHA-1 are:

Step1: Append padding bits.
• Add padding bits to the end of original message to prepare message in
multiple of 512 bits.
• Bits used in padding: 10000… (first is 1 followed by 00…)
• SHA-1 sequentially processes block of 512 bits of message
Step2: Append length.
• Padding remaining 64bits to make message length multiple of 512
bits.
last block of 512 bits
|64bits
• Now process each block
Step3: Initialize MD buffer:
• This is required, to hold intermediate values & final message digest.
• The size of this buffer is 160 bits.

• To handle 160 bits message digest, we need to have a registers. In SHA-1 there are
five registers named as
A
B
C
D
E
• Each & every register having capacity of 32bits. (Total 5*32 = 160 bits)
• We need to initialize this registers by 32 bits random hexadecimal value.

Step4: Process original message with the help of initialization registers(buffers).
• In this, we are having total 4 rounds.
• Each & every round is similar, but they are having their individual primitive
function.
• Each & every round having 20 steps.
• Each & every round have 3 things:
(i) Primitive function
(ii) Constant value, k
(iii) 20 bits world value
f1, k, w[0 – 19] <------- for first round.

f1, k, w[0 – 19]
f1, k, w[0 – 19]
f1, k, w[0 – 19]
f1, k, w[0 – 19]
First round

f1, k, w[0 – 19]
f1, k, w[0 – 19]
f1, k, w[0 – 19]
f1, k, w[0 – 19]
512 bits message
128bits
128bits
128bits
128bits

f1, k, w[0 – 19]
f1, k, w[0 – 19]
f1, k, w[0 – 19]
f1, k, w[0 – 19]
512 bits message
128bits(W0)
128bits
128bits
128bits
We are having five registers
A, B, C, D, E
Each having 32 bits hexadecimal
value. We need to proceed that
A B C D E
+ + + + +
160 bits message digest
Step5: Output
After all 512bits block have been
processed, the out from the nth stage is
the 160bits message digest.

SHA-1 MD-5
1. Message digest size 160bit Message Digest size 128bit
2. It is stronger against brute force
attack than MD-5
It is Weaker against brute force attack
than SHA-1
3. It is not vulnerable against
cryptanalyst.
It is vulnerable against cryptanalyst.
4. Slower than md-5 Faster than SHA-1
5 Perform 80 steps Perform 64 steps

Unit-III_3R-CRYPTO_2021-22_VSM.pptx

More Related Content

Similar to Unit-III_3R-CRYPTO_2021-22_VSM.pptx (20)

Recently uploaded (20)

Unit-III_3R-CRYPTO_2021-22_VSM.pptx