Vedran Peric's PhD Defense Presentation: Non-intrusive Methods for Mode Estimation in Power Systems using Synchrophasors
- 1. Non-intrusive Methods for Mode Estimation in Power Systems using Synchrophasors Vedran S. Perić March 15, 2016PhD Defense Presentation
- 2. Outline 1 • Oscillations – modes, ambient excitation 2 • Principles of mode estimation 3 • Optimal probing design and signal selection 4 • Mode estimation with non-white loads 5 • Prototype implementation 6 • Conclusions 2/28
- 3. Oscillations General phenomenon Excitation types Omnipresent random excitation (ambient) Intrinsic property of the system (modes) 3/28
- 4. Electromechanical oscillations in power systems ”The largest and most complex machine ever built by humankind” 4/28
- 5. 49.85 49.9 49.95 50 50.05 50.1 50.15 08:00:00 08:05:00 08:10:00 08:15:00 f[Hz] 20110219_0755-0825 Freq. Mettlen Freq. Brindisi Freq. Kassoe Why do we care ? PMU Data Oscillations if lightly damped can lead to a system black-out Occupy transmission capacities, increase losses, wear and tear February 19th 2011 – North-South Inter-Area Oscillation Continuously monitor frequency and damping 5/28
- 6. Application objectives Avoid black-outs Real-time monitoring Decision support tools Control actions 6/28
- 7. Outline 1 • Oscillations – ambient excitation, modes 2 • Principles of mode estimation 3 • Optimal probing design and signal selection 4 • Mode estimation with non-white loads 5 • Prototype implementation 6 • Conclusions 7/28
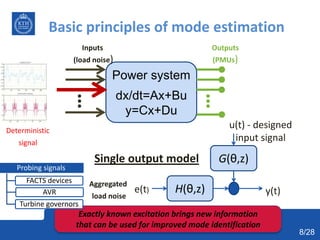
- 8. Basic principles of mode estimation Power system dx/dt=Ax+Bu y=Cx+Du Inputs (load noise) Outputs (PMUs) Deterministic signal Exactly known excitation brings new information that can be used for improved mode identification Probing signals FACTS devices AVR Turbine governors H(θ,z) G(θ,z) e(t) y(t) u(t) - designed input signal Aggregated load noise Single output model 8/28
- 9. Model structure of the power system o ARMAX o Box Jenkins Mathematical formulation Optimization problem: min 𝜃 1 𝑁 𝑡=1 𝑁 𝜀 𝑡, 𝜃 2 𝜀(𝑡, 𝜃) = 𝑦(𝑡) − 𝑦 ⌢ (𝑡|𝑡 − 1 Solution - identified model ( , ) ( , ) ( ) ( ) ( ) ( , ) ( , ) B z C z y t u t e t A z D z Contain information about the critical modes/poles 9/28
- 10. Model order selection Too low model order => bias of the estimate Too high model order => large variance/inaccuracy Data length Time resolutionvs Methods: Residual analysis Singular value analysis Akaike Information Criterion Variance-Accounted-For 10/28
- 11. Outline 1 • Oscillations – ambient excitation, modes 2 • Principles of mode estimation 3 • Optimal probing design and signal selection 4 • Mode estimation with non-white loads 5 • Prototype implementation 6 • Conclusions 11/28
- 12. Optimal probing – problem formulation Objective: Identify the critical damping ratio of G(z) 1 * * 0 0 0 02 1 ( , ) ( , ) ( , ) ( , ) 2 2 ( )u euu e N N P F F d F F d H(θ,z) G(θ,z) e(t) y(t) u(t) - input signal load measurement How should the probing signal look like ? 12/28 Spectrum influences accuracy 1 P Good estimate 1 P Bad estimate ( )u ( )u There is a limit how strong probing can be Stronger probing provides better accuracy
- 13. Spectrum calculation of the probing signal 1) Control effort 2) System disturbance 3) Accuracy Objective function 2 1 2 (t) min ( ) (s) ( ) 2 2u uu k k J d G d Constraint: var( ) T i i i e P e r r - tolerance Input power Output power (frequency deviation) Requirements : Optimization problem in a form of LMI The solution is the power spectrum of the probing signal 14/28
- 14. Time domain probing signal realization Spectrum calculation (solved) Time domain signal realization LMI Signal realization max var(ζ) Multisine ACF (rd) min(upeak 2 /urms 2 ) FIR filter min(║ r-rd║2 ) white noise - e(t) u(t) u(t) u(t) Probing Φu(ω) calculation 13/28
- 15. A method for probing signal realization Power spectrum ( ) ( ) m j r u des r m ACF r e 1 1 ( ) ( ) ( ) k k i ACF u i u i k 2 ( ) 0 ( ) ( ) M K k des u k min ACF ACF Sample autocorrelation Optimization Efficient recursive algorithm 15/28 Aimed probing autocorrelation General expression for autocorrelation Time domain signal as the decision variable
- 16. Optimal probing signal design results 0 0.5 1 1.5 2 2.5 0 5000 10000 15000 Frequency [Hz] Powerspectrum 0 0.5 1 1.5 2 2.5 0 1 2 3 4 x 10 5 Frequency [Hz] Powerspectrum Input spectrum parameterization White noise Multi-sine FIR filter var{u(t)} 10410.0 1441.58 1933.55 var{y(t)} 1.6761 1.598 1.5515 var{uy(t)} 6881.10 2318.81 2518.24 The same accuracy obtained with the 5-7 times weaker excitation The same input power provides 4-5 times better accuracy (0.25*10-5) Damping variance < 10-5 Benefits of the proposed method 16/28 KTH Nordic 32 Minimized input power Minimized disturbance2 critical modes 0.5Hz & 0.76Hz Reactive power probing
- 17. Optimal signal selection for mode estimation Only a few signals are sufficient for accurate estimation Large number of signals introduce bias and extensive computational effort Variance of the estimate describes estimation quality Compute asymptotic variance for each measured signal Rank the signals Select the top ones 1 * * 0 0 0 02 1 ( , ) ( , ) ( , ) ( , ) ( ) 2 2e e u u u N N P F F d F F d 1 * 0 0 ( , ) ( , ) 2 e e N P F F d 17/28
- 18. 49 48 50 17 40 31 18 42 44 47 0.09 0.1 0.11 0.12 0.13 0.14 0.15 1 2 3 4 5 6 7 8 9 10 Voltage angles 37 26 36 32 34 39 38 43 22 21 0.15 0.16 0.17 0.18 0.19 0.2 0.21 0.22 0.23 1 2 3 4 5 6 7 8 9 10 Voltage magnitudes Optimal signal selection results 18/28
- 19. Outline 1 • Oscillations – ambient excitation, modes 2 • Principles of mode estimation 3 • Optimal probing design and signal selection 4 • Mode estimation with non-white loads 5 • Prototype implementation 6 • Conclusions 19/28
- 20. Ambient mode estimation with non-white loads - Approach 20 Transmission/distribution border points have PMUs Non-white loads are inputs Input-output identification Source: EirGrid plc Transmission Distribution 20/28 Non-white noise excitation corrupts results of the classical mode estimators
- 21. Mode estimation considering spectral characteristics of load Direct closed loop identification Only modes of the transmission parts are identified 0 0.5 1 1.5 2 0.495 0.497 0.499 0.501 0.503 0.505 ModeFrequency[Hz] 0 0.5 1 1.5 2 2.5 3 0.495 0.497 0.499 0.501 0.503 0.505 0 0.5 1 1.5 2 1 1.8 2.6 3.4 4.2 5 0 0.5 1 1.5 2 2.5 3 1 1.8 2.6 3.4 4.2 5 Kpf ModeDamping[%] Mode frequency vs Mode frequency vs Kpf Mode damping vs Mode damping vs Kpf 𝑃𝐿 = 𝑃0 𝑉 𝑉0 𝛼 (1 + 𝐾 𝑝𝑓 𝛥𝑓) Transmission Load Power State (V,θ) Loads Independent disturbance (white noise) 21/28 Load effects are compensated afterwards
- 22. Results – Presence of forced oscillations 0 20 40 60 80 100 0 0.2 0.4 0.6 0.8 1 1.2 Damping ratio [%] Frequency[Hz] Estimated modes Real system modes 0 20 40 60 80 100 0 0.2 0.4 0.6 0.8 1 1.2 Damping ratio [%] Frequency[Hz] Estimated modes Real system modes Yule-Walker method Forced oscillation (0.45 Hz) 0 20 40 60 80 100 0 0.2 0.4 0.6 0.8 1 1.2 Damping ratio [%] Frequency[Hz] Estimated modes Real system modes N4SID method KTH Nordic32 system with forced oscillation at 0.45 Hz Monte Carlo simulations (large number of mode estimations) Classical methods: – Forced oscillation estimated as a critical mode – Real system mode masked by the forced oscillation Classical methods Proposed method 22/28 Proposed method discerns the forced oscillation
- 23. Results – white noise input When all assumptions used in classical mode estimators are fully satisfied All methods provide similar results 0 20 40 60 80 100 0 0.2 0.4 0.6 0.8 1 1.2 Damping ratio [%] Frequency[Hz] Estimated modes Real system modes 0 20 40 60 80 100 0 0.2 0.4 0.6 0.8 1 1.2 Damping ratio [%] Frequency[Hz] Estimated modes Real system modes 0 20 40 60 80 100 0 0.2 0.4 0.6 0.8 1 1.2 Damping ratio [%] Frequency[Hz] Estimated modes Real system modes Classical methods Yule-Walker method N4SID method Parameters Yule- Walker N4SID Proposed Method Mode1 Mean {f} [Hz] 0.4972 0.4978 0.4966 Mean {} [%] 3.3081 4.1213 3.8104 Var {f} 8.8670e-6 1.6260e-5 1.6592e-5 Var {} 0.2728 0.7942 0.8561 Mode2 Mean {f} [Hz] 0.7334 0.7309 0.7386 Mean {} [%] 3.8184 4.7095 3.5497 Var {f} 1.4072e-5 6.2711e-5 2.3151e-5 Var{} 0.3563 1.7925 0.5965 Proposed method 23/28
- 24. Outline 1 • Oscillations – ambient excitation, modes 2 • Principles of mode estimation 3 • Optimal probing design and signal selection 4 • Mode estimation with non-white loads 5 • Prototype implementation 6 • Conclusions 24/28
- 25. Power system or real-time simulator Phasor measurement units (PMUs). Phasor data concentrator (PDC) SDK PMU 1 PMU 2 PMU n PDC Comm. Network IEEE C37.118 Protocol KTH SmarTS Lab Wide Area Measurements System Real system Real time simulator User application Source Measurements Comm. Infrastructure Decoder Communication Network Software Development Kit (SDK) User applications 25/28
- 26. Prototype mode estimation application LabVIEW platform Real-life data The critical mode 0.39 Hz damping ratio 9 % (average) Other modes are observable at 0.2 Hz, 1 Hz and 1.4 Hz 0.5 Hz mode sporadically appears as a poorly damped mode 26/28
- 27. Conclusions A comprehensive way of dealing with mode estimation uncertainty. Probing when carefully designed provides a good mode estimation accuracy at low cost. Some signals provide better mode estimates than others. Quality signal criterion is proposed. A method that eliminates negative effects of non-white ambient excitation is proposed. Testing of the mode estimation tools needs to include other components of the system. 27/28





![49.85
49.9
49.95
50
50.05
50.1
50.15
08:00:00 08:05:00 08:10:00 08:15:00
f[Hz]
20110219_0755-0825
Freq. Mettlen Freq. Brindisi Freq. Kassoe
Why do we care ?
PMU Data
Oscillations if lightly damped can lead to a system black-out
Occupy transmission capacities, increase losses, wear and tear
February 19th 2011 – North-South Inter-Area Oscillation
Continuously monitor frequency and damping
5/28](https://image.slidesharecdn.com/phddefensev3-160315170623/85/Vedran-Peric-s-PhD-Defense-Presentation-Non-intrusive-Methods-for-Mode-Estimation-in-Power-Systems-using-Synchrophasors-5-320.jpg)









![Optimal probing signal design results
0 0.5 1 1.5 2 2.5
0
5000
10000
15000
Frequency [Hz]
Powerspectrum
0 0.5 1 1.5 2 2.5
0
1
2
3
4
x 10
5
Frequency [Hz]
Powerspectrum
Input spectrum parameterization
White noise Multi-sine FIR filter
var{u(t)} 10410.0 1441.58 1933.55
var{y(t)} 1.6761 1.598 1.5515
var{uy(t)} 6881.10 2318.81 2518.24
The same accuracy obtained with the 5-7 times weaker
excitation
The same input power provides 4-5 times better accuracy
(0.25*10-5)
Damping variance < 10-5
Benefits of
the proposed
method
16/28
KTH Nordic 32
Minimized
input power
Minimized
disturbance2 critical modes
0.5Hz & 0.76Hz
Reactive power
probing](https://image.slidesharecdn.com/phddefensev3-160315170623/85/Vedran-Peric-s-PhD-Defense-Presentation-Non-intrusive-Methods-for-Mode-Estimation-in-Power-Systems-using-Synchrophasors-16-320.jpg)




![Mode estimation considering spectral
characteristics of load
Direct closed loop identification
Only modes of the transmission
parts are identified
0 0.5 1 1.5 2
0.495
0.497
0.499
0.501
0.503
0.505
ModeFrequency[Hz]
0 0.5 1 1.5 2 2.5 3
0.495
0.497
0.499
0.501
0.503
0.505
0 0.5 1 1.5 2
1
1.8
2.6
3.4
4.2
5
0 0.5 1 1.5 2 2.5 3
1
1.8
2.6
3.4
4.2
5
Kpf
ModeDamping[%]
Mode frequency vs
Mode frequency vs Kpf
Mode damping vs
Mode damping vs Kpf
𝑃𝐿 = 𝑃0
𝑉
𝑉0
𝛼
(1 + 𝐾 𝑝𝑓 𝛥𝑓)
Transmission
Load Power State (V,θ)
Loads
Independent disturbance
(white noise)
21/28
Load effects are compensated
afterwards](https://image.slidesharecdn.com/phddefensev3-160315170623/85/Vedran-Peric-s-PhD-Defense-Presentation-Non-intrusive-Methods-for-Mode-Estimation-in-Power-Systems-using-Synchrophasors-21-320.jpg)
![Results – Presence of forced oscillations
0 20 40 60 80 100
0
0.2
0.4
0.6
0.8
1
1.2
Damping ratio [%]
Frequency[Hz]
Estimated modes
Real system modes
0 20 40 60 80 100
0
0.2
0.4
0.6
0.8
1
1.2
Damping ratio [%]
Frequency[Hz]
Estimated modes
Real system modes
Yule-Walker method
Forced oscillation (0.45 Hz)
0 20 40 60 80 100
0
0.2
0.4
0.6
0.8
1
1.2
Damping ratio [%]
Frequency[Hz]
Estimated modes
Real system modes
N4SID method
KTH Nordic32 system with forced oscillation at 0.45 Hz
Monte Carlo simulations (large number of mode estimations)
Classical methods:
– Forced oscillation estimated as a critical mode
– Real system mode masked by the forced oscillation
Classical methods Proposed method
22/28
Proposed method discerns the forced oscillation](https://image.slidesharecdn.com/phddefensev3-160315170623/85/Vedran-Peric-s-PhD-Defense-Presentation-Non-intrusive-Methods-for-Mode-Estimation-in-Power-Systems-using-Synchrophasors-22-320.jpg)
![Results – white noise input
When all assumptions used in
classical mode estimators are
fully satisfied
All methods provide similar
results
0 20 40 60 80 100
0
0.2
0.4
0.6
0.8
1
1.2
Damping ratio [%]
Frequency[Hz]
Estimated modes
Real system modes
0 20 40 60 80 100
0
0.2
0.4
0.6
0.8
1
1.2
Damping ratio [%]
Frequency[Hz]
Estimated modes
Real system modes
0 20 40 60 80 100
0
0.2
0.4
0.6
0.8
1
1.2
Damping ratio [%]
Frequency[Hz]
Estimated modes
Real system modes
Classical methods
Yule-Walker method N4SID method
Parameters
Yule-
Walker
N4SID
Proposed
Method
Mode1
Mean {f} [Hz] 0.4972 0.4978 0.4966
Mean {} [%] 3.3081 4.1213 3.8104
Var {f} 8.8670e-6 1.6260e-5 1.6592e-5
Var {} 0.2728 0.7942 0.8561
Mode2
Mean {f} [Hz] 0.7334 0.7309 0.7386
Mean {} [%] 3.8184 4.7095 3.5497
Var {f} 1.4072e-5 6.2711e-5 2.3151e-5
Var{} 0.3563 1.7925 0.5965
Proposed method
23/28](https://image.slidesharecdn.com/phddefensev3-160315170623/85/Vedran-Peric-s-PhD-Defense-Presentation-Non-intrusive-Methods-for-Mode-Estimation-in-Power-Systems-using-Synchrophasors-23-320.jpg)




