Y - Recursion The Hard Way GopherCon EU 2025
- 1. RECURSION THE HARD WAY Y ELEANOR MCHUGH @feyeleanor
- 2. Days of The Underground Walk on the Wild Side The Filthy Lucre Tour
- 3. DISCLAIMER experimental code and concepts ahead if it doesn't look idiomatic... it probably isn't all examples are for entertainment purposes only and may appear simpler than they really are tested exclusively on Intel MacBooks with go 1.24.4 do not do any of this on main! any resemblance to actual code & conceptstm - living or dead - is intentional github://feyeleanor/y_recursion_the_hard_way
- 4. FUNCTIONAL PROGRAMMING A DIFFERENT WAY OF CODING
- 5. ADD() IS A PURE FUNCTION - IT HAS NO SIDE EFFECTS package main import "os" func main() { os.Exit(add(3, 4)) } func add(x int, y int) int { return x + y } 01.GO github://feyeleanor/y_recursion_the_hard_way
- 6. GENERICS AND PURE FUNCTIONS MAKE A GREAT MATCH type Integer interface { ~int | ~int8 | ~int16 | ~int32 | ~int64 | ~uint | ~uint8 | ~uint16 | ~uint32 | ~uint64 } type Scalar interface { Integer | ~float32 | ~float64 } func main() { os.Exit(add(3, 4)) } func add[T Scalar](x, y T) T { return x + y } 02.GO github://feyeleanor/y_recursion_the_hard_way
- 7. GLOBAL VARIABLES INTRODUCE SIDE-EFFECTS func main() { for i, v := range os.Args[1:] { x, _ := strconv.Atoi(v) if i / 2 == 0 { sum += x } else { accumulate(x) } } os.Exit(sum) } var sum int func accumulate(x int) { sum += x } 04.GO github://feyeleanor/y_recursion_the_hard_way
- 8. AN IMPURE FUNCTION HAS SIDE-EFFECTS func main() { for _, v := range os.Args[1:] { x, _ := strconv.Atoi(v) accumulate(x) } os.Exit(accumulate(0)) } var sum int func accumulate(x int) int { sum += x return sum } 05.GO github://feyeleanor/y_recursion_the_hard_way
- 9. OBJECT METHODS CAN ALSO HAVE SIDE-EFFECTS func main() { for _, v := range os.Args[1:] { x, _ := strconv.Atoi(v) a.Add(x) } os.Exit(int(a)) } var a Accumulator type Accumulator int func (a *Accumulator) Add(x int) { *a += Accumulator(x) } 06.GO github://feyeleanor/y_recursion_the_hard_way
- 10. FUNCTION CLOSURES ALLOW PRIVATE SIDE-EFFECTS func main() { a := MakeAccumulator() for _, v := range os.Args[1:] { x, _ := strconv.Atoi(v) a(x) } os.Exit(a(0)) } type Accumulator func(int) int func MakeAccumulator() Accumulator { var sum int return func(x int) int { sum += x return sum } } 07.GO github://feyeleanor/y_recursion_the_hard_way
- 11. A FUNCTION WITH PRIVATE SIDE-EFFECTS CAN ALSO BE AN OBJECT func main() { a := MakeAccumulator[int]() for _, v := range os.Args[1:] { x, _ := strconv.Atoi(v) a(x) } os.Exit(a.Int()) } type Accumulator[T Scalar] func(T) T func MakeAccumulator[T Scalar]() Accumulator[T] { var sum T return func(x T) T { sum += x return sum } } func (a Accumulator[T]) Int() int { return int(a(0)) } 08.GO github://feyeleanor/y_recursion_the_hard_way
- 12. A FUNCTION WITH PRIVATE SIDE-EFFECTS CAN ALSO BE AN OBJECT func main() { var n []int for _, v := range os.Args[1:] { x, _ := strconv.Atoi(v) n = append(n, x) } os.Exit(MakeAccumulator(n...).Int()) } func MakeAccumulator[T Scalar](s ...T) (a Accumulator[T]) { var sum T a = func(x T) T { sum += x return sum } for _, v := range s { a.Add(v) } return } func (a Accumulator[T]) Add(x any) Accumulator[T] { switch x := x.(type) { case T: a(x) case Accumulator[T]: a(x(0)) } return a } 09.GO github://feyeleanor/y_recursion_the_hard_way
- 13. OBJECTS CAN BE DEFINED BY CONCRETE OR STRUCTURAL TYPE func main() { var n []int for _, v := range os.Args[1:] { x, _ := strconv.Atoi(v) n = append(n, x) } os.Exit(MakeAccumulator(n...).Int()) } type Intish interface { Int() int } func (a Accumulator[T]) Int() int { return int(a(0)) } func (a Accumulator[T]) Add(x any) Accumulator[T] { switch x := x.(type) { case T: a(x) case Intish: a(T(x.Int())) } return a } 10.GO github://feyeleanor/y_recursion_the_hard_way
- 14. RECURSION FUNCTIONS THAT CALL THEMSELVES
- 15. A RECURSIVE FUNCTION CALLS ITSELF UNTIL STACK SPACE RUNS OUT package main func main() { main() } 11.GO github://feyeleanor/y_recursion_the_hard_way
- 16. CALL STACK EXHAUSTION IS A NON-RECOVERABLE PANIC package main func main() { defer func() { recover() }() main() } 12.GO github://feyeleanor/y_recursion_the_hard_way
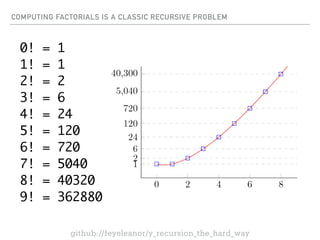
- 17. 0! = 1 1! = 1 2! = 2 3! = 6 4! = 24 5! = 120 6! = 720 7! = 5040 8! = 40320 9! = 362880 COMPUTING FACTORIALS IS A CLASSIC RECURSIVE PROBLEM github://feyeleanor/y_recursion_the_hard_way
- 18. COMPUTING FACTORIALS IS A CLASSIC RECURSIVE PROBLEM github://feyeleanor/y_recursion_the_hard_way
- 19. COMPUTING FACTORIALS IS A CLASSIC RECURSIVE PROBLEM github://feyeleanor/y_recursion_the_hard_way
- 20. COMPUTING FACTORIALS IS A CLASSIC RECURSIVE PROBLEM github://feyeleanor/y_recursion_the_hard_way
- 21. COMPUTING MULTIPLE FACTORIALS WITH RECURSION func main() { for _, v := range os.Args[1:] { if x, e := strconv.Atoi(v); e != nil || x < 0 { fmt.Printf("no factorial defined for %vn", v) } else { fmt.Printf("%v! = %vn", x, Factorial(x)) } } } func Factorial[T Integer](n T) T { if n == 0 { return 1 } return n * Factorial(n - 1) } 16.GO github://feyeleanor/y_recursion_the_hard_way
- 22. COMPUTING MULTIPLE FACTORIALS WITH RECURSION func main() { for _, v := range os.Args[1:] { if x, e := strconv.Atoi(v); e != nil || x < 0 { fmt.Printf("no factorial defined for %vn", v) } else { fmt.Printf("%v! = %vn", x, Factorial(x)) } } } func Factorial[T Integer](n T) T { if n == 0 { return 1 } return n * Factorial(n - 1) } 16.GO github://feyeleanor/y_recursion_the_hard_way
- 23. COMPUTING MULTIPLE FACTORIALS WITH RECURSION func main() { for _, v := range os.Args[1:] { if x, e := strconv.Atoi(v); e != nil || x < 0 { fmt.Printf("no factorial defined for %vn", v) } else { fmt.Printf("%v! = %vn", x, Factorial(x)) } } } func Factorial[T Integer](n T) T { if n == 0 { return 1 } return n * Factorial(n - 1) } 16.GO github://feyeleanor/y_recursion_the_hard_way
- 24. COMPUTING MULTIPLE FACTORIALS WITH RECURSION AND EXCEPTIONS func main() { for _, v := range os.Args[1:] { func() { defer func() { if x := recover(); x != nil { fmt.Printf("no factorial defined for %vn", x) } }() if x, e := strconv.Atoi(v); e == nil && x > -1 { fmt.Printf("%v! = %vn", x, Factorial(x)) } else { panic(v) } }() } } 19.GO github://feyeleanor/y_recursion_the_hard_way
- 25. SIMPLE COMPOSITION WITH HIGHER ORDER FUNCTIONS func main() { skipUndefined := Catch(func() { if x := recover(); x != nil { fmt.Printf("no factorial defined for %vn", x) } }) for _, v := range os.Args[1:] { skipUndefined(func() { if x, e := strconv.Atoi(v); e == nil && x > -1 { fmt.Printf("%v! = %vn", x, Factorial(x)) } else { panic(v) } }) } } func Catch(e func()) func(func()) { return func(f func()) { defer e() f() } } 20.GO github://feyeleanor/y_recursion_the_hard_way
- 26. SIMPLE COMPOSITION WITH HIGHER ORDER FUNCTIONS func main() { skipUndefined := Catch(func() { if x := recover(); x != nil { fmt.Printf("no factorial defined for %vn", x) } }) for _, v := range os.Args[1:] { skipUndefined(func() { if x, e := strconv.Atoi(v); e == nil && x > -1 { fmt.Printf("%v! = %vn", x, Factorial(x)) } else { panic(v) } }) } } func Catch(e func()) func(func()) { return func(f func()) { defer e() f() } } 20.GO github://feyeleanor/y_recursion_the_hard_way
- 27. SIMPLE COMPOSITION WITH CURRYING AND HIGHER ORDER FUNCTIONS func main() { skipUndefined := Catch(func() { if x := recover(); x != nil { fmt.Printf("no factorial defined for %vn", x) } }) for _, v := range os.Args[1:] { skipUndefined(func() { if x, e := strconv.Atoi(v); e == nil && x > -1 { fmt.Printf("%v! = %vn", x, Factorial(x)) } else { panic(v) } }) } } func Catch(e func()) func(func()) { return func(f func()) { defer e() f() } } 20.GO github://feyeleanor/y_recursion_the_hard_way
- 28. SIMPLE COMPOSITION WITH CURRYING func main() { skipUndefined := Catch(NoDefinedValue("factorial")) for _, v := range os.Args[1:] { skipUndefined(func() { if x, e := strconv.Atoi(v); e == nil && x > -1 { fmt.Printf("%v! = %vn", x, Factorial(x)) } else { panic(v) } }) } } func Catch(e func()) func(func()) { return func(f func()) { defer e() f() } } func NoDefinedValue(s string) func() { return func() { if x := recover(); x != nil { fmt.Printf("no %v defined for %vn", s, x) } } } 21.GO github://feyeleanor/y_recursion_the_hard_way
- 29. SIMPLE COMPOSITION WITH CURRYING func main() { skipUndefined := Catch(NoDefinedValue("factorial")) for _, v := range os.Args[1:] { skipUndefined(PrintFactorial(v)) } } func PrintFactorial(v string) func() { return func() { if x, e := strconv.Atoi(v); e == nil && x > -1 { fmt.Printf("%v! = %vn", x, Factorial(x)) } else { panic(v) } } } 22.GO github://feyeleanor/y_recursion_the_hard_way
- 30. SIMPLE COMPOSITION WITH ANONYMOUS FUNCTIONS func main() { skipUndefined := Catch(NoDefinedValue("factorial")) for _, v := range os.Args[1:] { skipUndefined( PrintFactorial(v)) } } func main() { for _, v := range os.Args[1:] { func(f func()) { defer func(s string) { if x := recover(); x != nil { fmt.Printf("no %v defined for %vn", s, x) } }("factorial") f() }(func() { if x, e := strconv.Atoi(v); e == nil && x > -1 { fmt.Printf("%v! = %vn", x, Factorial(x)) } else { panic(v) } }) } } github://feyeleanor/y_recursion_the_hard_way is equivalent to
- 31. USING HIGHER ORDER FUNCTIONS FOR ITERATION func main() { skipUndefined := Catch(NoDefinedValue("factorial")) Each(os.Args[1:], func(v string) { skipUndefined(PrintFactorial(v)) }) } func Each[T any](s []T, f func(T)) { if len(s) > 0 { f(s[0]) Each(s[1:], f) } } 23.GO github://feyeleanor/y_recursion_the_hard_way
- 32. USING HIGHER ORDER FUNCTIONS TO CACHE RESULTS func main() { f := MakeFactorial[int]() skipUndefined := Catch(NoDefinedValue("factorial")) Each(os.Args[1:], func(v string) { skipUndefined(PrintResult(v, f)) }) } func MakeFactorial[T Integer]() (f func(T) T) { c := map[T] T { 0: 1 } return func(n T) (r T) { if n < 0 { panic(n) } if r = c[n]; r == 0 { r = n * f(n - 1) } c[n] = r return } } func PrintResult[T Integer](v string, f func(T) T) func() { return func() { if x, e := strconv.Atoi(v); e == nil { fmt.Printf("f(%v) = %vn", x, f(T(x))) } else { panic(v) } } } 24.GO github://feyeleanor/y_recursion_the_hard_way
- 34. A RECURSIVE FUNCTION CALLS ITSELF package main func main() { main() } 11.GO github://feyeleanor/y_recursion_the_hard_way this recurses because main() is a named function
- 35. A RECURSIVE FUNCTION CALLS ITSELF package main func main() { func(x) { ... } } github://feyeleanor/y_recursion_the_hard_way but how do we make an anonymous function recurse?
- 36. ANONYMOUS FUNCTIONS AND THE LAMBDA CALCULUS github://feyeleanor/y_recursion_the_hard_way
- 37. A FIXED POINT IS WHEN A FUNCTION RETURNS THE VALUE PASSED TO IT so given f(x) = x2 - 3x + 4 f(2) = 2 is a fi xed point meaning that calculating f for a value returns that value unchanged github://feyeleanor/y_recursion_the_hard_way in untyped lambda calculus functions are anonymous but every function has a fi xed point which is not the general case in mathematics
- 38. INTRODUCING THE Y COMBINATOR Y g = (λf.(λx.f (x x)) (λx.f (x x))) g = (λx.g (x x)) (λx.g (x x)) = g ((λx.g (x x)) (λx.g (x x))) = g (Y g) the Y combinator uses fi xed points to express recursion for an anonymous function github://feyeleanor/y_recursion_the_hard_way
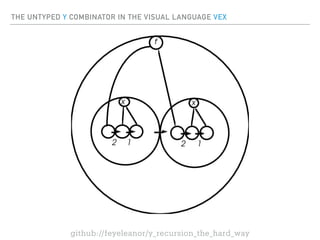
- 39. THE UNTYPED Y COMBINATOR IN THE VISUAL LANGUAGE VEX github://feyeleanor/y_recursion_the_hard_way
- 40. THE UNTYPED Y COMBINATOR IN THE VISUAL LANGUAGE VEX github://feyeleanor/y_recursion_the_hard_way wtf?
- 41. ANONYMOUS FUNCTIONS AND THE LAMBDA CALCULUS github://feyeleanor/y_recursion_the_hard_way
- 42. THE UNTYPED Y COMBINATOR func main() { skipUndefined := Catch(NoDefinedValue("factorial")) factorial := Y(func(h any) any { return func(n any) (r any) { if n, ok := n.(int); ok { switch { case n == 0, n == 1: return 1 case n > 1: return n * h.(func(any) any)(n-1).(int) } } panic(n) } }) Each(os.Args[1:], func(v string) { skipUndefined(PrintResult(v, factorial)) }) } func PrintResult(v string, f func(any) any) func() { return func() { if x, e := strconv.Atoi(v); e == nil { fmt.Printf("f(%v) = %vn", x, f(x)) } else { panic(v) } } } 25.GO github://feyeleanor/y_recursion_the_hard_way
- 43. THE UNTYPED Y COMBINATOR func main() { skipUndefined := Catch(NoDefinedValue("factorial")) factorial := Y(func(h any) any { return func(n any) (r any) { if n, ok := n.(int); ok { switch { case n == 0, n == 1: return 1 case n > 1: return n * h.(func(any) any)(n-1).(int) } } panic(n) } }) Each(os.Args[1:], func(v string) { skipUndefined(PrintResult(v, factorial)) }) } func Y(g func(any) any) func(any) any { return func(f any) func(any) any { return f.(func(any) any)(f).(func(any) any) }(func(f any) any { return g(func(x any) any { return f.(func(any) any)(f).(func(any) any)(x) }) }) } 25.GO github://feyeleanor/y_recursion_the_hard_way
- 44. THE UNTYPED Y COMBINATOR func main() { skipUndefined := Catch(NoDefinedValue("factorial")) factorial := Y(func(h any) any { return func(n any) (r any) { if n, ok := n.(int); ok { switch { case n == 0, n == 1: return 1 case n > 1: return n * h.(func(any) any)(n-1).(int) } } panic(n) } }) Each(os.Args[1:], func(v string) { skipUndefined(PrintResult(v, factorial)) }) } func Y(g func(any) any) func(any) any { return func(f any) func(any) any { return f.(func(any) any)(f).(func(any) any) }(func(f any) any { return g(func(x any) any { return f.(func(any) any)(f).(func(any) any)(x) }) }) } 25.GO github://feyeleanor/y_recursion_the_hard_way
- 45. THE UNTYPED Y COMBINATOR func main() { skipUndefined := Catch(NoDefinedValue("factorial")) factorial := Y(func(h any) any { return func(n any) (r any) { if n, ok := n.(int); ok { switch { case n == 0, n == 1: return 1 case n > 1: return n * h.(func(any) any)(n-1).(int) } } panic(n) } }) Each(os.Args[1:], func(v string) { skipUndefined(PrintResult(v, factorial)) }) } func Y(g func(any) any) func(any) any { return func(f any) func(any) any { return f.(func(any) any)(f).(func(any) any) }(func(f any) any { return g(func(x any) any { return f.(func(any) any)(f).(func(any) any)(x) }) }) } 25.GO github://feyeleanor/y_recursion_the_hard_way
- 46. THE UNTYPED Y COMBINATOR func main() { skipUndefined := Catch(NoDefinedValue("factorial")) factorial := Y(func(h any) any { return func(n any) (r any) { ... } }) Each(os.Args[1:], func(v string) { skipUndefined(PrintResult(v, factorial)) }) } func main() { Each(os.Args[1:], func(v string) { Catch(NoDefinedValue("factorial"))( PrintResult(v, Y(func(h any) any { return func(n any) (r any) { ... } }))) }) } github://feyeleanor/y_recursion_the_hard_way is equivalent to
- 47. INTRODUCING GO TYPES TO THE Y COMBINATOR type Function func(any) any func Recursor(f any) Function { return f.(func(any) any)(f).(func(any) any) } func Y(g Function) Function { return Recursor( func(f any) any { return g(func(x any) any { return Recursor(f)(x) }) }) } func PrintResult(v string, f Function) func() { return func() { if x, e := strconv.Atoi(v); e == nil { fmt.Printf("f(%v) = %vn", x, f(x)) } else { panic(v) } } } 26.GO github://feyeleanor/y_recursion_the_hard_way
- 48. INTRODUCING GO TYPES TO THE Y COMBINATOR type Function func(any) any func Recursor(f any) Function { return f.(func(any) any)(f).(func(any) any) } func Y(g Function) Function { return Recursor( func(f any) any { return g(func(x any) any { return Recursor(f)(x) }) }) } 26.GO github://feyeleanor/y_recursion_the_hard_way
- 49. INTRODUCING GO TYPES TO THE Y COMBINATOR type Transformer func(Function) Function func Recursor(f Function) Function { return f(f).(Function) } func Y(g Transformer) Function { return Recursor( func(f any) any { return g(func(x any) any { return Recursor(f.(Function))(x) }) }) } 27.GO github://feyeleanor/y_recursion_the_hard_way
- 50. INTRODUCING GO TYPES TO THE Y COMBINATOR type Transformer func(Function) Function func Recursor(f Function) Function { return f(f).(Function) } func Y(g Transformer) Function { return Recursor( func(f any) any { return g(func(x any) any { return Recursor(f.(Function))(x) }) }) } 27.GO github://feyeleanor/y_recursion_the_hard_way
- 51. INTRODUCING GO TYPES TO THE Y COMBINATOR type Transformer func(Function) Function func main() { ... factorial := Y(func(h Function) Function { return func(n any) (r any) { if n, ok := n.(int); ok { switch { case n == 0, n == 1: return 1 case n > 1: return n * h(n-1).(int) } } panic(n) } }) ... } func Y(g Transformer) Function { return Recursor( func(f any) any { return g(func(x any) any { return Recursor(f.(Function))(x) }) }) } 27.GO github://feyeleanor/y_recursion_the_hard_way
- 52. SIMPLIFYING THE TYPED Y COMBINATOR Y g = (λf.(λx.f (x x)) (λx.f (x x))) g = (λx.g (x x)) (λx.g (x x)) = g ((λx.g (x x)) (λx.g (x x))) = g (Y g) github://feyeleanor/y_recursion_the_hard_way
- 53. SIMPLIFYING THE TYPED Y COMBINATOR type Function func(any) any type Transformer func(Function) Function type Recursor func(Recursor) Function func (r Recursor) Apply(t Transformer) Function { return t(r(r)) } func Y(t Transformer) Function { g := func(r Recursor) Function { return func(x any) any { return r.Apply(t)(x) } } return g(g) } 28.GO github://feyeleanor/y_recursion_the_hard_way
- 54. THE Y COMBINATOR WITH GENERIC TYPES type Function[T, R any] func(T) R type Transformer[T, R any] func(Function[T, R]) Function[T, R] type Recursor[T, R any] func(Recursor[T, R]) Function[T, R] func (r Recursor[T, R]) Apply(t Transformer[T, R]) Function[T, R] { return t(r(r)) } func PrintResult[T, R Integer](v string, f Function[T, R]) func() { return func() { if x, e := strconv.Atoi(v); e == nil { fmt.Printf("f(%v) = %vn", x, f(T(x))) } else { panic(v) } } } 29.GO github://feyeleanor/y_recursion_the_hard_way
- 55. THE Y COMBINATOR WITH GENERIC TYPES type Function[T, R any] func(T) R type Transformer[T, R any] func(Function[T, R]) Function[T, R] type Recursor[T, R any] func(Recursor[T, R]) Function[T, R] func (r Recursor[T, R]) Apply(t Transformer[T, R]) Function[T, R] { return t(r(r)) } func main() { ... factorial := Y(func(h Function[int, int]) Function[int, int] { return func(n int) (r int) { switch { case n < 0: panic(n) case n > 1: return n * h(n - 1) } return 1 } }) ... } 29.GO github://feyeleanor/y_recursion_the_hard_way
- 56. THE GENERIC Y COMBINATOR WITH AUTOMATIC RESULT CACHING func Y[T comparable, R any](t Transformer[T, R]) Function[T, R] { m := make(map[T]R) g := func(r Recursor[T, R]) Function[T, R] { return func(x T) (v R) { var ok bool if v, ok = m[x]; ok { return v } v = r.Apply(t)(x) m[x] = v fmt.Printf("Y: setting m[%v] = %vn", x, v) return v } } return g(g) } 30.GO github://feyeleanor/y_recursion_the_hard_way
- 57. THE GENERIC Y COMBINATOR WITH AUTOMATIC RESULT CACHING func Y[T comparable, R any](t Transformer[T, R]) Function[T, R] { m := make(map[T]R) g := func(r Recursor[T, R]) Function[T, R] { return func(x T) (v R) { var ok bool if v, ok = m[x]; ok { return v } v = r.Apply(t)(x) m[x] = v fmt.Printf("Y: setting m[%v] = %vn", x, v) return v } } return g(g) } 30.GO github://feyeleanor/y_recursion_the_hard_way
- 58. THE GENERIC Y COMBINATOR WITH AUTOMATIC RESULT CACHING func MakeY[T comparable, R any](m map[T]R) func(Transformer[T, R]) Function[T, R] { return func(t Transformer[T, R]) Function[T, R] { g := func(r Recursor[T, R]) Function[T, R] { return func(x T) (v R) { var ok bool if v, ok = m[x]; ok { return v } v = r.Apply(t)(x) m[x] = v fmt.Printf("Y: setting m[%v] = %vn", x, v) return v } } return g(g) } } 31.GO github://feyeleanor/y_recursion_the_hard_way
- 59. THE GENERIC Y COMBINATOR WITH AUTOMATIC RESULT CACHING func main() { skipUndefined := Catch(NoDefinedValue("factorial")) factorial := func(h Function[int, int]) Function[int, int] { return func(n int) (r int) { switch { case n < 0: panic(n) case n > 1: return n * h(n - 1) } return 1 } } m := make(map[int]int) Each(os.Args[1:], func(v string) { skipUndefined(PrintResult(v, MakeY(m)(factorial))) }) Each(os.Args[1:], func(v string) { skipUndefined(PrintResult(v, MakeY(m)(factorial))) }) } 31.GO github://feyeleanor/y_recursion_the_hard_way
- 62. LEANPUB://GONOTEBOOK [GITHUB | SLIDESHARE]://FEYELEANOR






 T {
return x + y
}
02.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-6-320.jpg)
![GLOBAL VARIABLES INTRODUCE SIDE-EFFECTS
func main() {
for i, v := range os.Args[1:] {
x, _ := strconv.Atoi(v)
if i / 2 == 0 {
sum += x
} else {
accumulate(x)
}
}
os.Exit(sum)
}
var sum int
func accumulate(x int) {
sum += x
}
04.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-7-320.jpg)
![AN IMPURE FUNCTION HAS SIDE-EFFECTS
func main() {
for _, v := range os.Args[1:] {
x, _ := strconv.Atoi(v)
accumulate(x)
}
os.Exit(accumulate(0))
}
var sum int
func accumulate(x int) int {
sum += x
return sum
}
05.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-8-320.jpg)
![OBJECT METHODS CAN ALSO HAVE SIDE-EFFECTS
func main() {
for _, v := range os.Args[1:] {
x, _ := strconv.Atoi(v)
a.Add(x)
}
os.Exit(int(a))
}
var a Accumulator
type Accumulator int
func (a *Accumulator) Add(x int) {
*a += Accumulator(x)
}
06.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-9-320.jpg)
![FUNCTION CLOSURES ALLOW PRIVATE SIDE-EFFECTS
func main() {
a := MakeAccumulator()
for _, v := range os.Args[1:] {
x, _ := strconv.Atoi(v)
a(x)
}
os.Exit(a(0))
}
type Accumulator func(int) int
func MakeAccumulator() Accumulator {
var sum int
return func(x int) int {
sum += x
return sum
}
}
07.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-10-320.jpg)
![A FUNCTION WITH PRIVATE SIDE-EFFECTS CAN ALSO BE AN OBJECT
func main() {
a := MakeAccumulator[int]()
for _, v := range os.Args[1:] {
x, _ := strconv.Atoi(v)
a(x)
}
os.Exit(a.Int())
}
type Accumulator[T Scalar] func(T) T
func MakeAccumulator[T Scalar]() Accumulator[T] {
var sum T
return func(x T) T {
sum += x
return sum
}
}
func (a Accumulator[T]) Int() int {
return int(a(0))
}
08.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-11-320.jpg)
![A FUNCTION WITH PRIVATE SIDE-EFFECTS CAN ALSO BE AN OBJECT
func main() {
var n []int
for _, v := range os.Args[1:] {
x, _ := strconv.Atoi(v)
n = append(n, x)
}
os.Exit(MakeAccumulator(n...).Int())
}
func MakeAccumulator[T Scalar](s ...T) (a Accumulator[T]) {
var sum T
a = func(x T) T {
sum += x
return sum
}
for _, v := range s {
a.Add(v)
}
return
}
func (a Accumulator[T]) Add(x any) Accumulator[T] {
switch x := x.(type) {
case T:
a(x)
case Accumulator[T]:
a(x(0))
}
return a
}
09.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-12-320.jpg)
![OBJECTS CAN BE DEFINED BY CONCRETE OR STRUCTURAL TYPE
func main() {
var n []int
for _, v := range os.Args[1:] {
x, _ := strconv.Atoi(v)
n = append(n, x)
}
os.Exit(MakeAccumulator(n...).Int())
}
type Intish interface {
Int() int
}
func (a Accumulator[T]) Int() int {
return int(a(0))
}
func (a Accumulator[T]) Add(x any) Accumulator[T] {
switch x := x.(type) {
case T:
a(x)
case Intish:
a(T(x.Int()))
}
return a
}
10.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-13-320.jpg)






![COMPUTING MULTIPLE FACTORIALS WITH RECURSION
func main() {
for _, v := range os.Args[1:] {
if x, e := strconv.Atoi(v); e != nil || x < 0 {
fmt.Printf("no factorial defined for %vn", v)
} else {
fmt.Printf("%v! = %vn", x, Factorial(x))
}
}
}
func Factorial[T Integer](n T) T {
if n == 0 {
return 1
}
return n * Factorial(n - 1)
}
16.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-21-320.jpg)
![COMPUTING MULTIPLE FACTORIALS WITH RECURSION
func main() {
for _, v := range os.Args[1:] {
if x, e := strconv.Atoi(v); e != nil || x < 0 {
fmt.Printf("no factorial defined for %vn", v)
} else {
fmt.Printf("%v! = %vn", x, Factorial(x))
}
}
}
func Factorial[T Integer](n T) T {
if n == 0 {
return 1
}
return n * Factorial(n - 1)
}
16.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-22-320.jpg)
![COMPUTING MULTIPLE FACTORIALS WITH RECURSION
func main() {
for _, v := range os.Args[1:] {
if x, e := strconv.Atoi(v); e != nil || x < 0 {
fmt.Printf("no factorial defined for %vn", v)
} else {
fmt.Printf("%v! = %vn", x, Factorial(x))
}
}
}
func Factorial[T Integer](n T) T {
if n == 0 {
return 1
}
return n * Factorial(n - 1)
}
16.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-23-320.jpg)
![COMPUTING MULTIPLE FACTORIALS WITH RECURSION AND EXCEPTIONS
func main() {
for _, v := range os.Args[1:] {
func() {
defer func() {
if x := recover(); x != nil {
fmt.Printf("no factorial defined for %vn", x)
}
}()
if x, e := strconv.Atoi(v); e == nil && x > -1 {
fmt.Printf("%v! = %vn", x, Factorial(x))
} else {
panic(v)
}
}()
}
}
19.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-24-320.jpg)
![SIMPLE COMPOSITION WITH HIGHER ORDER FUNCTIONS
func main() {
skipUndefined := Catch(func() {
if x := recover(); x != nil {
fmt.Printf("no factorial defined for %vn", x)
}
})
for _, v := range os.Args[1:] {
skipUndefined(func() {
if x, e := strconv.Atoi(v); e == nil && x > -1 {
fmt.Printf("%v! = %vn", x, Factorial(x))
} else {
panic(v)
}
})
}
}
func Catch(e func()) func(func()) {
return func(f func()) {
defer e()
f()
}
}
20.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-25-320.jpg)
![SIMPLE COMPOSITION WITH HIGHER ORDER FUNCTIONS
func main() {
skipUndefined := Catch(func() {
if x := recover(); x != nil {
fmt.Printf("no factorial defined for %vn", x)
}
})
for _, v := range os.Args[1:] {
skipUndefined(func() {
if x, e := strconv.Atoi(v); e == nil && x > -1 {
fmt.Printf("%v! = %vn", x, Factorial(x))
} else {
panic(v)
}
})
}
}
func Catch(e func()) func(func()) {
return func(f func()) {
defer e()
f()
}
}
20.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-26-320.jpg)
![SIMPLE COMPOSITION WITH CURRYING AND HIGHER ORDER FUNCTIONS
func main() {
skipUndefined := Catch(func() {
if x := recover(); x != nil {
fmt.Printf("no factorial defined for %vn", x)
}
})
for _, v := range os.Args[1:] {
skipUndefined(func() {
if x, e := strconv.Atoi(v); e == nil && x > -1 {
fmt.Printf("%v! = %vn", x, Factorial(x))
} else {
panic(v)
}
})
}
}
func Catch(e func()) func(func()) {
return func(f func()) {
defer e()
f()
}
}
20.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-27-320.jpg)
![SIMPLE COMPOSITION WITH CURRYING
func main() {
skipUndefined := Catch(NoDefinedValue("factorial"))
for _, v := range os.Args[1:] {
skipUndefined(func() {
if x, e := strconv.Atoi(v); e == nil && x > -1 {
fmt.Printf("%v! = %vn", x, Factorial(x))
} else {
panic(v)
}
})
}
}
func Catch(e func()) func(func()) {
return func(f func()) {
defer e()
f()
}
}
func NoDefinedValue(s string) func() {
return func() {
if x := recover(); x != nil {
fmt.Printf("no %v defined for %vn", s, x)
}
}
}
21.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-28-320.jpg)
![SIMPLE COMPOSITION WITH CURRYING
func main() {
skipUndefined := Catch(NoDefinedValue("factorial"))
for _, v := range os.Args[1:] {
skipUndefined(PrintFactorial(v))
}
}
func PrintFactorial(v string) func() {
return func() {
if x, e := strconv.Atoi(v); e == nil && x > -1 {
fmt.Printf("%v! = %vn", x, Factorial(x))
} else {
panic(v)
}
}
}
22.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-29-320.jpg)
![SIMPLE COMPOSITION WITH ANONYMOUS FUNCTIONS
func main() {
skipUndefined := Catch(NoDefinedValue("factorial"))
for _, v := range os.Args[1:] {
skipUndefined(
PrintFactorial(v))
}
}
func main() {
for _, v := range os.Args[1:] {
func(f func()) {
defer func(s string) {
if x := recover(); x != nil {
fmt.Printf("no %v defined for %vn", s, x)
}
}("factorial")
f()
}(func() {
if x, e := strconv.Atoi(v); e == nil && x > -1 {
fmt.Printf("%v! = %vn", x, Factorial(x))
} else {
panic(v)
}
})
}
}
github://feyeleanor/y_recursion_the_hard_way
is equivalent to](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-30-320.jpg)
![USING HIGHER ORDER FUNCTIONS FOR ITERATION
func main() {
skipUndefined := Catch(NoDefinedValue("factorial"))
Each(os.Args[1:], func(v string) {
skipUndefined(PrintFactorial(v))
})
}
func Each[T any](s []T, f func(T)) {
if len(s) > 0 {
f(s[0])
Each(s[1:], f)
}
}
23.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-31-320.jpg)
![USING HIGHER ORDER FUNCTIONS TO CACHE RESULTS
func main() {
f := MakeFactorial[int]()
skipUndefined := Catch(NoDefinedValue("factorial"))
Each(os.Args[1:], func(v string) {
skipUndefined(PrintResult(v, f))
})
}
func MakeFactorial[T Integer]() (f func(T) T) {
c := map[T] T { 0: 1 }
return func(n T) (r T) {
if n < 0 {
panic(n)
}
if r = c[n]; r == 0 {
r = n * f(n - 1)
}
c[n] = r
return
}
}
func PrintResult[T Integer](v string, f func(T) T) func() {
return func() {
if x, e := strconv.Atoi(v); e == nil {
fmt.Printf("f(%v) = %vn", x, f(T(x)))
} else {
panic(v)
}
}
}
24.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-32-320.jpg)








![THE UNTYPED Y COMBINATOR
func main() {
skipUndefined := Catch(NoDefinedValue("factorial"))
factorial := Y(func(h any) any {
return func(n any) (r any) {
if n, ok := n.(int); ok {
switch {
case n == 0, n == 1:
return 1
case n > 1:
return n * h.(func(any) any)(n-1).(int)
}
}
panic(n)
}
})
Each(os.Args[1:], func(v string) {
skipUndefined(PrintResult(v, factorial))
})
}
func PrintResult(v string, f func(any) any) func() {
return func() {
if x, e := strconv.Atoi(v); e == nil {
fmt.Printf("f(%v) = %vn", x, f(x))
} else {
panic(v)
}
}
}
25.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-42-320.jpg)
![THE UNTYPED Y COMBINATOR
func main() {
skipUndefined := Catch(NoDefinedValue("factorial"))
factorial := Y(func(h any) any {
return func(n any) (r any) {
if n, ok := n.(int); ok {
switch {
case n == 0, n == 1:
return 1
case n > 1:
return n * h.(func(any) any)(n-1).(int)
}
}
panic(n)
}
})
Each(os.Args[1:], func(v string) {
skipUndefined(PrintResult(v, factorial))
})
}
func Y(g func(any) any) func(any) any {
return func(f any) func(any) any {
return f.(func(any) any)(f).(func(any) any)
}(func(f any) any {
return g(func(x any) any {
return f.(func(any) any)(f).(func(any) any)(x)
})
})
}
25.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-43-320.jpg)
![THE UNTYPED Y COMBINATOR
func main() {
skipUndefined := Catch(NoDefinedValue("factorial"))
factorial := Y(func(h any) any {
return func(n any) (r any) {
if n, ok := n.(int); ok {
switch {
case n == 0, n == 1:
return 1
case n > 1:
return n * h.(func(any) any)(n-1).(int)
}
}
panic(n)
}
})
Each(os.Args[1:], func(v string) {
skipUndefined(PrintResult(v, factorial))
})
}
func Y(g func(any) any) func(any) any {
return func(f any) func(any) any {
return f.(func(any) any)(f).(func(any) any)
}(func(f any) any {
return g(func(x any) any {
return f.(func(any) any)(f).(func(any) any)(x)
})
})
}
25.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-44-320.jpg)
![THE UNTYPED Y COMBINATOR
func main() {
skipUndefined := Catch(NoDefinedValue("factorial"))
factorial := Y(func(h any) any {
return func(n any) (r any) {
if n, ok := n.(int); ok {
switch {
case n == 0, n == 1:
return 1
case n > 1:
return n * h.(func(any) any)(n-1).(int)
}
}
panic(n)
}
})
Each(os.Args[1:], func(v string) {
skipUndefined(PrintResult(v, factorial))
})
}
func Y(g func(any) any) func(any) any {
return func(f any) func(any) any {
return f.(func(any) any)(f).(func(any) any)
}(func(f any) any {
return g(func(x any) any {
return f.(func(any) any)(f).(func(any) any)(x)
})
})
}
25.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-45-320.jpg)
![THE UNTYPED Y COMBINATOR
func main() {
skipUndefined := Catch(NoDefinedValue("factorial"))
factorial := Y(func(h any) any {
return func(n any) (r any) {
...
}
})
Each(os.Args[1:], func(v string) {
skipUndefined(PrintResult(v, factorial))
})
}
func main() {
Each(os.Args[1:], func(v string) {
Catch(NoDefinedValue("factorial"))(
PrintResult(v, Y(func(h any) any {
return func(n any) (r any) {
...
}
})))
})
}
github://feyeleanor/y_recursion_the_hard_way
is equivalent to](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-46-320.jpg)







![THE Y COMBINATOR WITH GENERIC TYPES
type Function[T, R any] func(T) R
type Transformer[T, R any] func(Function[T, R]) Function[T, R]
type Recursor[T, R any] func(Recursor[T, R]) Function[T, R]
func (r Recursor[T, R]) Apply(t Transformer[T, R]) Function[T, R] {
return t(r(r))
}
func PrintResult[T, R Integer](v string, f Function[T, R]) func() {
return func() {
if x, e := strconv.Atoi(v); e == nil {
fmt.Printf("f(%v) = %vn", x, f(T(x)))
} else {
panic(v)
}
}
}
29.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-54-320.jpg)
![THE Y COMBINATOR WITH GENERIC TYPES
type Function[T, R any] func(T) R
type Transformer[T, R any] func(Function[T, R]) Function[T, R]
type Recursor[T, R any] func(Recursor[T, R]) Function[T, R]
func (r Recursor[T, R]) Apply(t Transformer[T, R]) Function[T, R] {
return t(r(r))
}
func main() {
...
factorial := Y(func(h Function[int, int]) Function[int, int] {
return func(n int) (r int) {
switch {
case n < 0:
panic(n)
case n > 1:
return n * h(n - 1)
}
return 1
}
})
...
}
29.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-55-320.jpg)
 Function[T, R] {
m := make(map[T]R)
g := func(r Recursor[T, R]) Function[T, R] {
return func(x T) (v R) {
var ok bool
if v, ok = m[x]; ok {
return v
}
v = r.Apply(t)(x)
m[x] = v
fmt.Printf("Y: setting m[%v] = %vn", x, v)
return v
}
}
return g(g)
}
30.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-56-320.jpg)
 Function[T, R] {
m := make(map[T]R)
g := func(r Recursor[T, R]) Function[T, R] {
return func(x T) (v R) {
var ok bool
if v, ok = m[x]; ok {
return v
}
v = r.Apply(t)(x)
m[x] = v
fmt.Printf("Y: setting m[%v] = %vn", x, v)
return v
}
}
return g(g)
}
30.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-57-320.jpg)
 func(Transformer[T, R]) Function[T, R] {
return func(t Transformer[T, R]) Function[T, R] {
g := func(r Recursor[T, R]) Function[T, R] {
return func(x T) (v R) {
var ok bool
if v, ok = m[x]; ok {
return v
}
v = r.Apply(t)(x)
m[x] = v
fmt.Printf("Y: setting m[%v] = %vn", x, v)
return v
}
}
return g(g)
}
}
31.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-58-320.jpg)
![THE GENERIC Y COMBINATOR WITH AUTOMATIC RESULT CACHING
func main() {
skipUndefined := Catch(NoDefinedValue("factorial"))
factorial := func(h Function[int, int]) Function[int, int] {
return func(n int) (r int) {
switch {
case n < 0:
panic(n)
case n > 1:
return n * h(n - 1)
}
return 1
}
}
m := make(map[int]int)
Each(os.Args[1:], func(v string) {
skipUndefined(PrintResult(v, MakeY(m)(factorial)))
})
Each(os.Args[1:], func(v string) {
skipUndefined(PrintResult(v, MakeY(m)(factorial)))
})
}
31.GO
github://feyeleanor/y_recursion_the_hard_way](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-59-320.jpg)


![LEANPUB://GONOTEBOOK [GITHUB | SLIDESHARE]://FEYELEANOR](https://image.slidesharecdn.com/2025y-recursionthehardwayredux-250618101849-ec704641/85/Y-Recursion-The-Hard-Way-GopherCon-EU-2025-62-320.jpg)